尋路演算法-貪婪最佳優先演算法

貓冬發表於2017-12-16

最近開始接觸尋路演算法，對此不太瞭解的話建議讀者先看這篇文章《如何快速找到最優路線？深入理解遊戲中尋路演算法》。

所有尋路演算法都需要一種方法以數學的方式估算某個節點是否應該被選擇。大多數遊戲都會使用啟發式 （heuristic），以 h(x) 表示，就是估算從某個位置到目標位置的開銷。理想情況下，啟發式結果越接近真實越好。

——《遊戲程式設計演算法與技巧》

今天主要說的是貪婪最佳優先搜尋（Greedy Best-First Search），貪心演算法的含義是：求解問題時，總是做出在當前來說最好的選擇。通俗點說就是，這是一個“短視”的演算法。

為什麼說是“短視”呢？首先要明白一個概念：曼哈頓距離。

曼哈頓距離

曼哈頓距離被認為不能沿著對角線移動，如下圖中，紅、藍、黃線都代表等距離的曼哈頓距離。綠線代表歐氏距離，如果地圖允許對角線移動的話，曼哈頓距離會經常比歐式距離高。

在 2D 地圖中，曼哈頓距離的計算如下：

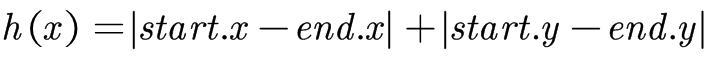
貪婪最佳優先搜尋的簡介

貪婪最佳優先搜尋的每一步，都會查詢相鄰的節點，計算它們距離終點的曼哈頓距離，即最低開銷的啟發式。

貪婪最佳優先搜尋在障礙物少的時候足夠的快，但最佳優先搜尋得到的都是次優的路徑。例如下圖，演算法不斷地尋找當前 h（啟發式）最小的值，但這條路徑很明顯不是最優的。

貪婪最佳優先搜尋“未能遠謀”，大多數遊戲都要比貪婪最佳優先演算法所能提供的更好的尋路，但大多數尋路演算法都是基於貪婪演算法，所以瞭解該演算法很有必要。

首先是節點類，每個節點需要儲存上一個節點的引用和 h 值，其他資訊是為了方便演算法的實現。儲存上一個節點的引用是為了像一個連結串列一樣，最後能通過引用得到路徑中所有的節點。

public class Node
{
    // 上一個節點
    public Node parent;
    // 節點的 h(x) 值
    public float h;
    // 與當前節點相鄰的節點
    public List<Node> adjecent = new List<Node>();
    // 節點所在的行
    public int row;
    // 節點所在的列
    public int col;
    // 清除節點資訊
    public void Clear()
    {
        parent = null;
        h = 0.0f;
    }
}

下面是圖類，圖類最主要的任務就是根據提供的二維陣列初始化所有的節點，包括尋找他們的相鄰節點。

// 圖類
public class Graph
{
    public int rows = 0;
    public int cols = 0;
    public Node[] nodes;

    public Graph(int[, ] grid)
    {
        rows = grid.GetLength(0);
        cols = grid.GetLength(1);

        nodes = new Node[grid.Length];
        for (int i = 0; i < nodes.Length; i++)
        {
            Node node = new Node();
            node.row = i / cols;
            node.col = i - (node.row * cols);
            nodes[i] = node;
        }

        // 找到每一個節點的相鄰節點
        foreach (Node node in nodes)
        {
            int row = node.row;
            int col = node.col;
            // 牆，即節點不能通過的格子 
            // 1 為牆，0 為可通過的格子
            if (grid[row, col] != 1)
            {
                // 上方的節點
                if (row > 0 && grid[row - 1, col] != 1)
                {
                    node.adjecent.Add(nodes[cols * (row - 1) + col]);
                }
                // 右邊的節點
                if (col < cols - 1 && grid[row, col + 1] != 1)
                {
                    node.adjecent.Add(nodes[cols * row + col + 1]);
                }

                // 下方的節點
                if (row < rows - 1 && grid[row + 1, col] != 1)
                {
                    node.adjecent.Add(nodes[cols * (row + 1) + col]);
                }

                // 左邊的節點
                if (col > 0 && grid[row, col - 1] != 1)
                {
                    node.adjecent.Add(nodes[cols * row + col - 1]);
                }
            }
        }
    }
}

在演算法類中，我們需要記錄開放集合和封閉集合。開放集合指的是當前步驟我們需要考慮的節點，例如演算法開始時就要考慮初始節點的相鄰節點，並從其找到最低的 h(x) 值開銷的節點。封閉集合存放已經計算過的節點。

// 開放集合
public List<Node> reachable;
// 封閉集合，存放已經被演算法估值的節點
public List<Node> explored;

下面是演算法主要的邏輯，額外的函式可以檢視專案原始碼。

public Stack<Node> Finding()
{
    // 存放查詢路徑的棧
    Stack<Node> path;
    Node currentNode = reachable[0];
    // 迭代查詢，直至找到終點節點
    while (currentNode != destination)
    {
        explored.Add(currentNode);
        reachable.Remove(currentNode);
        // 將當前節點的相鄰節點加入開放集合
        AddAjacent(currentNode);
        // 查詢了相鄰節點後依然沒有可以考慮的節點，查詢失敗。
        if (reachable.Count == 0)
        {
            return null;
        }
        // 將開放集合中h值最小的節點當做當前節點
        currentNode = FindLowestH();
    }
    // 查詢成功，則根據節點parent找到查詢到的路徑
    path = new Stack<Node>();
    Node node = destination;
    // 先將終點壓入棧，再迭代地把node的前一個節點壓入棧
    path.Push(node);
    while (node.parent != null)
    {
        path.Push(node.parent);
        node = node.parent;
    }
    return path;
}

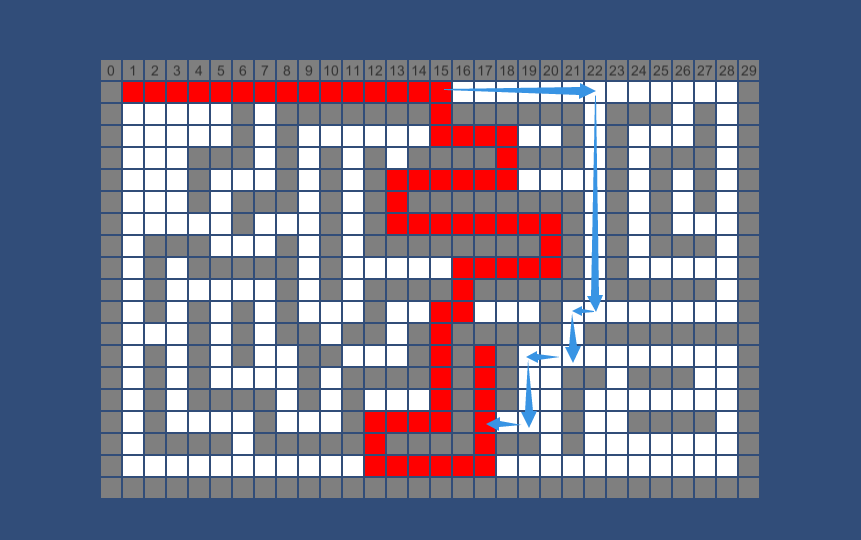
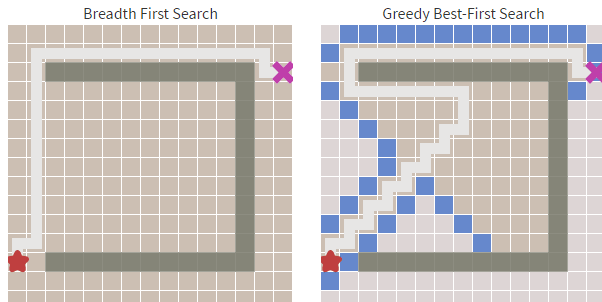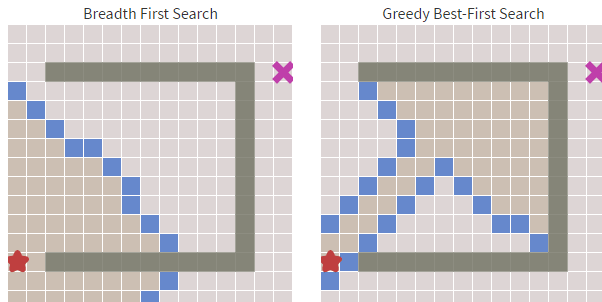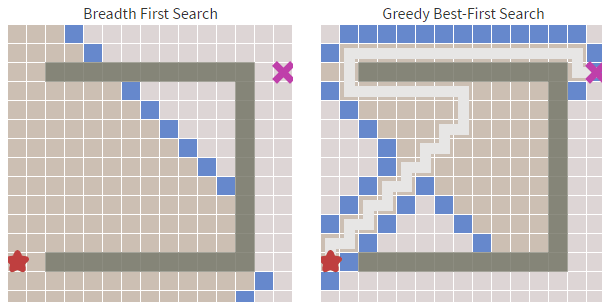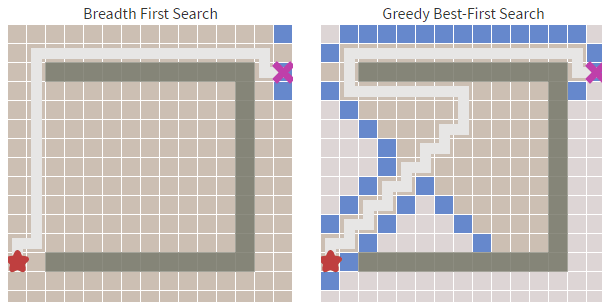
除此以外還有些展示演算法的類，程式碼不在這裡展出。下面是演算法執行的截圖，其中白色格子為可走的格子，灰色格子是不可穿越的，紅色格子為查詢到的路徑，左上角格子為查詢起點，右上角格子為查詢終點。

small