3D列印技術之切片引擎（2）

【此係列文章基於熔融沉積( fused depostion modeling, FDM )成形工藝】

在上一篇文章中，我從總體上介紹了一下切片引擎技術，從這一篇文章開始，我開始說一下具體的技術細節。

切片引擎，實體部分包括：

提取邊界向量——>新增多邊——>生成填充向量集合。

為了避免實體和地板的粘連有時候還需要生成個底座，以及為了避免列印頭停止列印後有繼續吐絲的現象而影響到列印質量，有時候也需要新增牆結構，這些都是很工程的問題，開發上難度也很低，這裡就不贅述。

除之外就是支撐部分。這篇文章就先說下支撐演算法。

生成支撐向量集合分為人工生成和自動生成兩種，優越的支撐演算法主要體現在

1，省材料。

2，生成速度快。

3，生成的支撐體與零件實體較少的接觸與干涉，有利於剝離。

4，支撐能穩固的支撐住任意結構的模型。

其中，3和4互斥，要在兩者做出一個平衡；支撐體與實體干涉太少必然就不夠穩固，當列印到上層的時候就容易使實體和地板的連線處鬆動以及實體部分塌陷等等，這要在開發中做到儘量的兩者兼顧，要在保證4的情況下儘量的實現3。

畢竟，切片引擎的優劣主要體現在實體生成質量，支撐演算法僅僅是錦上添花，對於國內的大多數剛剛起步的3D列印企業目前還沒有必要把過多的精力放在支撐演算法的研發上。

在我的切片引擎中我用的三維布林運算，採用線掃描，取樣間隔大於實體的取樣間隔。

這樣的方案不是最好的，但是可以在開發週期和軟體質量方面做出一個平衡。

具體方案如下：

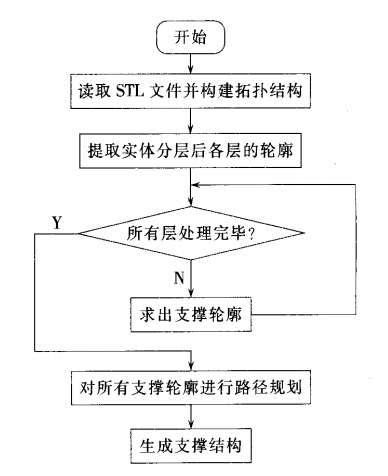
將原型零件的STL模型上所有法向量Z向分量為負的三角形面片合併成支撐區域，再分別將各區域沿Z軸向基底投影，從而得到所需支撐的STL模型。如果投影區域與零件模型的實體有相交區域，還需要對生成的支撐進行干涉處理，其中要用到三維布林運算。具體流程如下圖：

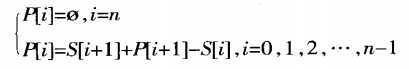
我認為較好的方案是在一篇國內的論文當中反映的：

 

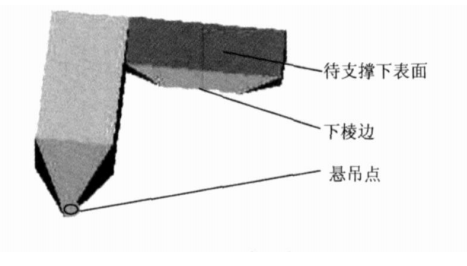
上圖是描述零件待支撐的區域，當且僅當發現對應模型的某一部位有傾斜角度過大的下表面、下稜線和懸吊點這3種結構特徵之一時,應該對其加以支撐；其他情況一律不加支撐。由於STL檔案是三角形面片的無序集合,無法由其直接知道不同三角形之間的連線關係,不利於後續待支撐區域的識別和分層等處理,所以先應在無序三角形基礎上建立其鄰接關係,即拓撲資訊。也就是說要識別出懸吊點，下稜邊和傾斜角過大的下表面。傾斜角過大的下表面每一層切片對應位置都需要新增支撐，而懸吊點和下稜邊只需要對周圍較小的鄰域內的層新增支撐。

通常根據三角面片的法向向量與z軸正向的夾角大小對STL模型中三角面片進行分類,大於90度的三角形稱為下表面三角形,小於90度的稱為上表面三角形,正好等於90度的為垂直面三角形。傾斜角度過大的下表面是由法向向量與z軸正向的夾角大於某一閾值(不同成形機系統對應的閾值大小也不同)的三角形連線而成的區域。先將法向向量與z軸正向的夾角大於某一閾值的待支撐三角形找出來,並將彼此共點或共邊相鄰的三角形合併成各個獨立的面域即得到了待支撐的下表面。下稜邊至少包含在1個下表面三角形中,且包含該邊的三角形中第3點的z座標均大於這條邊2個端點的z座標,將彼此共點相鄰的下稜邊合併成各條獨立的下稜線。懸吊點也至少包含在1個下表面三角形中,且該點鄰接三角形中另外2點的z座標均大於這個點的z座標,則確定該點為懸吊點。