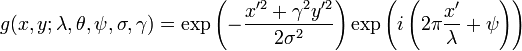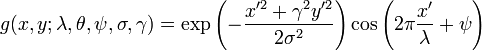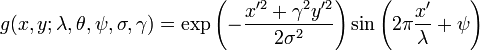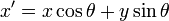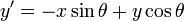Gabor濾波器學習

  本文的目的是用C實現生成Gabor模版，並對影像卷積。並簡單提一下，Gabor濾波器在紋理特徵提取上的應用。

一、什麼是Gabor函式（以下內容含部分翻譯自維基百科）

  在影像處理中，Gabor函式是一個用於邊緣提取的線性濾波器。Gabor濾波器的頻率和方向表達同人類視覺系統類似。研究發現，Gabor濾波器十分適合紋理表達和分離。在空間域中，一個二維Gabor濾波器是一個由正弦平面波調製的高斯核函式。

  還有，生物學實驗發現，Gabor濾波器可以很好地近似單細胞的感受野函式（光強刺激下的傳遞函式），什麼視皮層內的超柱，bla...bla，總之是這方面仿生的數學模型。

  另外，網上有一種說法，gabor分為實部和虛部，用實部進行濾波後影像會平滑；虛部濾波後用來檢測邊緣。【來自百度知道某個大神的回答】，我查了文獻，發現的確有人用Gabor的奇函式部分做邊緣提取（《基於Gabor濾波器的邊緣檢測演算法》 無線電工程 2000年第3卷第30期）。另外，從我的實驗結果也有類似的發現。暫且認為這個對的吧。

  Gabor濾波器的脈衝響應，可以定義為一個正弦波（對於二維Gabor濾波器是正弦平面波）乘以高斯函式。由於乘法卷積性質，Gabor濾波器的脈衝響應的傅立葉變換是其調和函式的傅立葉變換和高斯函式傅立葉變換的卷積。該濾波器由實部和虛部組成，二者相互正交。一組不同頻率不同方向的Gabor函式陣列對於影像特徵提取非常有用。

下面給出二維Gabor函式的數學表達：

複數表達：

實數部分：

虛數部分：

   

其中：

和

下面介紹公式中各個引數的含義，及引數如何配置問題【都從老外那翻譯來的】：

波長（λ）：它的值以畫素為單位指定，通常大於等於2.但不能大於輸入影像尺寸的五分之一。

方向（θ）：這個引數指定了Gabor函式並行條紋的方向，它的取值為0到360度

相位偏移（φ）：它的取值範圍為-180度到180度。其中，0he180度分別對應中心對稱的center-on函式和center-off函式，而-90度和90度對應反對稱函式。

長寬比（γ）：空間縱橫比，決定了Gabor函式形狀（support，我翻譯為形狀）的橢圓率（ellipticity）。當γ= 1時，形狀是圓的。當γ< 1時，形狀隨著平行條紋方向而拉長。通常該值為0.5

頻寬（b）：Gabor濾波器的半響應空間頻率頻寬b和σ/ λ的比率有關，其中σ表示Gabor函式的高斯因子的標準差，如下：

σ的值不能直接設定，它僅隨著頻寬b變化。頻寬值必須是正實數，通常為1，此時，標準差和波長的關係為：σ= 0.56 λ。頻寬越小，標準差越大，Gabor形狀越大，可見平行興奮和抑制區條紋數量越多。

下面給出，不同引數配置下的Gabor核函式效果圖，大小均100*100：

a.波長對比組【方向為：0，相位偏移量為：0，縱橫比率為：0.5，頻寬為：1，下圖波長分別為5，10，15】

b.方向對比組【波長為：10，相位偏移量為：0，空間縱橫比為：0.5，頻寬為：1，方向分別為：0，45，90】

c.相位偏移量對比組【波長為：10，方向為：0，空間縱橫比：0.5，頻寬：1，相位偏移量分別為：0，180，-90，90】

d.空間縱橫比對比組【波長：10，相位偏移量：0，方向：0，頻寬：1，空間縱橫比分別為：0.5，1】

e.頻寬對比組【波長：10，方向：0，相位偏移量：0，空間縱橫比：0.5，頻寬分別為：0.5，1，2】

二、gabor函式實現：

matlab版本，我從pudn上找來的，但他的gabor函式，我沒怎麼看明白：

gabor函式：

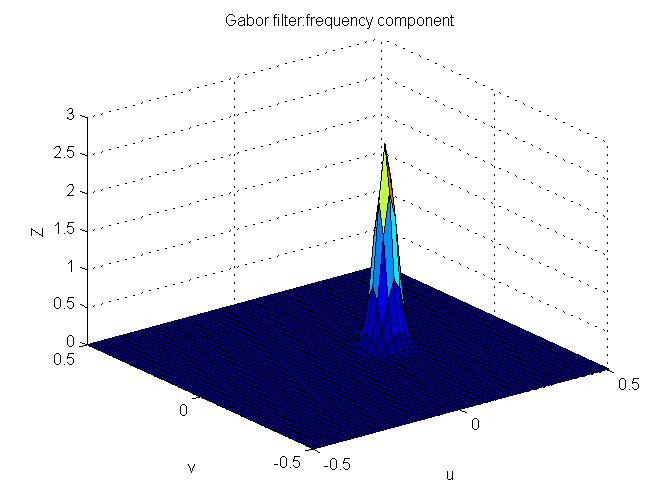
function gabor_k = compute(x,y,f0,theta)
r = 1; g = 1;
x1 = x*cos(theta) + y*sin(theta);
y1 = -x*sin(theta) + y*cos(theta);
gabor_k = f0^2/(pi*r*g)*exp(-(f0^2*x1^2/r^2+f0^2*y1^2/g^2))*exp(i*2*pi*f0*x1); 

%繪製一個Gabor濾波器的空域和頻域函式圖
clear;
x = 0;
theta = 0;
f0 = 0.2;
for i = linspace(-15,15,50)
    x = x + 1;
    y = 0;
    for j = linspace(-15,15,50)
        y = y + 1;
        z(y,x)=compute(i,j,f0,theta);
    end
end
x = linspace(-15,15,50);
y = linspace(-15,15,50);
surf(x,y,real(z))
title('Gabor filter:real component');
xlabel('x');
ylabel('y');
zlabel('z');
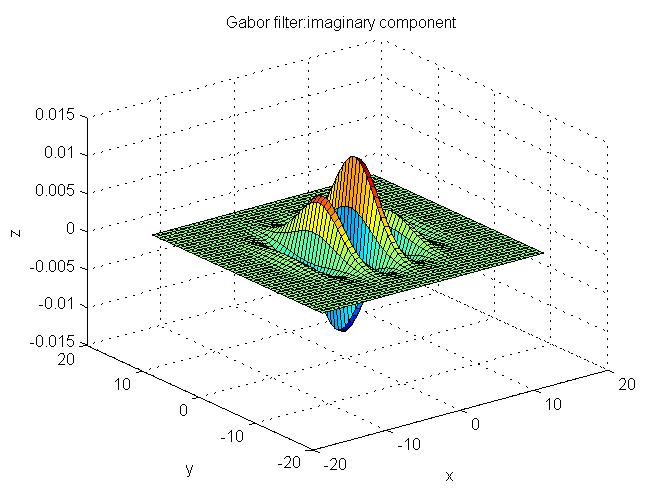
figure(2);
surf(x,y,imag(z))
title('Gabor filter:imaginary component');
xlabel('x');
ylabel('y');
zlabel('z');

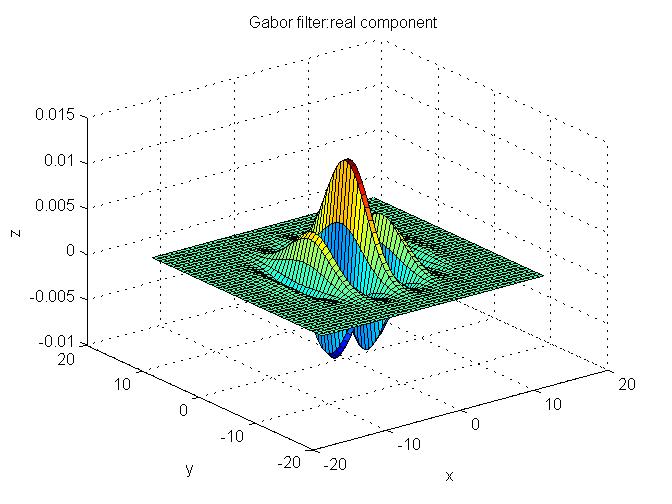
Z = fft2(z);
u = linspace(-0.5,0.5,50);
v = linspace(-0.5,0.5,50);
figure(3);
surf(u,v,abs(fftshift(Z)))
title('Gabor filter:frequency component');
xlabel('u');
ylabel('v');
zlabel('Z');

執行結果：

   

%4個方向的Gabo濾波器通過影像顯示
clear;
x = 0;
theta = pi*3/4;%用弧度0,pi/4,pi/2,pi*3/4
f0 = 0.2; 
for i = linspace(-15,15,50)
    x = x + 1;
    y = 0;
    for j = linspace(-15,15,50)
        y = y + 1;
        z(y,x)=compute(i,j,f0,theta);
    end
end
z_real = real(z);
m = min(z_real(:));
z_real = z_real+abs(m);
M = max(z_real(:));
imshow(1/M*z_real);
figure(2)
z_imag = imag(z);
m = min(z_imag(:));
z_imag = z_imag+abs(m);
M = max(z_imag(:));
imshow(1/M*z_imag);

執行效果：

實數部分：

虛數部分：

%4個方向的Gabor濾波器對lena進行濾波
clear;
I = imread('.\pic\lena.bmp');
f0 = 0.2; 
count = 0;
for theta = [0,pi/4,pi/2,pi*3/4];%用弧度0,pi/4,pi/2,pi*3/4
    count = count + 1;
    x = 0;
    for i = linspace(-8,8,11)
        x = x + 1;
        y = 0;
        for j = linspace(-8,8,11)
            y = y + 1;
            z(y,x)=compute(i,j,f0,theta);
        end
    end
    figure(count);
    filtered = filter2(z,I,'valid');
    f = abs(filtered);
    imshow(f/max(f(:)))
end

執行效果：

好吧，不管他了。大概感受一下吧。由於我沒看明白他的gabor函式怎麼定義的，引數設定也不一樣，實驗結果很不相同，我希望我是對的，天地良心吶！！我只能按照維基百科給出的函式，編寫了以下C程式碼：

// my_gabor.cpp : 定義控制檯應用程式的入口點。
//

#include "stdafx.h"
#include<iostream>
#include <opencv2/core/core.hpp>  
#include <opencv2/highgui/highgui.hpp>  
#include <opencv2/imgproc/imgproc.hpp>
#include "math.h"
#define  PI 3.1415926
#define  N 4
using namespace std;
using namespace cv;

void m_filer(double *src,int height,int width,double *mask_rel,double *mask_img,int mW,int mH,int k)
{
	IplImage *tmp;
	double a,b,c;
	char res[20];		//儲存的影像名稱

	tmp = cvCreateImage(cvSize(width,height),IPL_DEPTH_8U,1);

	for (int i = 0;i < height;i++)
	{
		for (int j = 0;j < width;j++)
		{
			a = 0.0;
			b = 0.0;
			c = 0.0;
			//去掉靠近邊界的行列，無法濾波，超出範圍
			if (i > int(mH/2) && i < height - int(mH/2) && j > int(mW) && j < width - int(mW/2))
			{
				for (int m = 0;m < mH;m++)
				{
					for(int n = 0;n < mW;n++)
					{
						//printf("%f\n",src[(i+m-int(mH/2))*width+(j+n-int(mW))]);
						a += src[(i+m-int(mH/2))*width+(j+n-int(mW))]*mask_rel[m*mW+n];
						b += src[(i+m-int(mH/2))*width+(j+n-int(mW))]*mask_img[m*mW+n];
						//printf("%f,%f\n",a,b);
					}
				}
			}
			c = sqrt(a*a+b*b);
			c /= mW*mH;
			tmp->imageData[i*width+j] = (unsigned char)c;
		}
	}
	sprintf(res,"result%d.jpg",k);
	cvSaveImage(res,tmp);
	cvReleaseImage(&tmp);
}

int _tmain(int argc, _TCHAR* argv[])
{
	IplImage *src;
	double *rel,*img,*src_data,xtmp,ytmp,tmp1,tmp2,tmp3,re,im;
	double Theta,sigma,Gamma,Lambda,Phi;		//公式中的5個引數
	int gabor_height,gabor_width,x,y;

	src = cvLoadImage("test.jpg",CV_LOAD_IMAGE_GRAYSCALE);
	gabor_height = 10;
	gabor_width = 10;
	Gamma = 1.0;
	Lambda = 10.0;
	sigma = 100;
	Phi = 0;

	rel = (double *)malloc(sizeof(double)*gabor_width*gabor_height);//實數部分
	img = (double *)malloc(sizeof(double)*gabor_width*gabor_height);//虛數部分
	src_data = (double *)malloc(sizeof(double)*src->widthStep*src->height);	//影像資料 

	for (int i=0;i<src->height;i++)
	{
		for (int j=0;j<src->widthStep;j++)
		{
			src_data[i*src->widthStep+j]=(unsigned char)src->imageData[i*src->widthStep+j];
			//printf("%f\n",src_data[i*src->widthStep+j]);
		}
	}

	//構造gabor函式
	for (int k = 0;k < N;k++)					//定義N方向
	{
		Theta = PI*((double)k/N);
		for (int i = 0;i < gabor_height;i++)	//定義模版大小
		{
			for (int j = 0;j < gabor_width;j++)
			{
				x = j - gabor_width/2;
				y = i - gabor_height/2;

				xtmp = (double)x*cos(Theta) + (double)y*sin(Theta);
				ytmp = (double)y*cos(Theta) - (double)x*sin(Theta);

				tmp1 = exp(-(pow(xtmp,2)+pow(ytmp*Gamma,2))/(2*pow(sigma,2)));
				tmp2 = cos(2*PI*xtmp/Lambda + Phi);
				tmp3 = sin(2*PI*xtmp/Lambda + Phi);
				
				re = tmp1*tmp2;
				im = tmp1*tmp3;

				rel[i*gabor_width+j] = re;
				img[i*gabor_width+j] = im;
				//printf("%f,%f\n",re,im);
			}
		}
		//用不同方向的GABOR函式對影像濾波並儲存圖片
		m_filer(src_data,src->height,src->width,rel,img,10,10,k);
	}
	
	free(rel);free(img);free(src_data);
	return 0;
}

執行效果：

      

大概就這樣湊活吧。我這邊實數部分和虛數部分的處理是採用求模的方式。有問題的，請廣大人民群眾提出來啊。

三、用gabor提取紋理特徵的思路【抄別人的論文】

  Gabor濾波方法的主要思想是：不同紋理一般具有不同的中心頻率及頻寬，根據這些頻率和頻寬可以設計一組Gabor濾波器對紋理影像進行濾波，每個Gabor濾波器只允許與其頻率相對應的紋理順利通過，而使其他紋理的能量受到抑制，從各濾波器的輸出結果中分析和提取紋理特徵，用於之後的分類或分割任務。Gabor濾波器提取紋理特徵主要包括兩個過程：①設計濾波器(例如函式、數目、方向和間隔)；②從濾波器的輸出結果中提取有效紋理特徵集。Gabor濾波器是帶通濾波器，它的單位衝激響應函式(Gabor函式)是高斯函式與復指數函的乘積。它是達到時頻測不準關係下界的函式，具有最好地兼顧訊號在時頻域的分辨能力。

  實現步驟：

（1）將輸入影像分為3×3（9塊）和4×4（16塊）的影像塊；

（2）建立Gabor濾波器組：選擇4個尺度，6個方向，這樣組成了24個Gabor濾波器；

（3）Gabor濾波器組與每個影像塊在空域卷積，每個影像塊可以得到24個濾波器輸出，這       些輸出是影像塊大小的影像，如果直接將其作為特徵向量，特徵空間的維數會很大，       所以需要“濃縮”；

（4）每個影像塊經過Gabor濾波器組的24個輸出，要“濃縮”（文中提到“average filter        responses within the block”我的理解是取灰度均值）為一個24×1的列向量作為該影像       塊的紋理特徵。查閱相關文獻，發現也可以用方差。

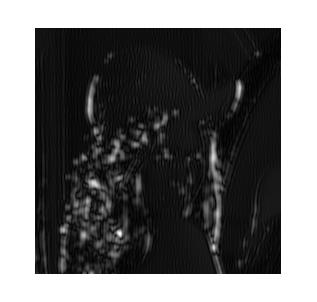
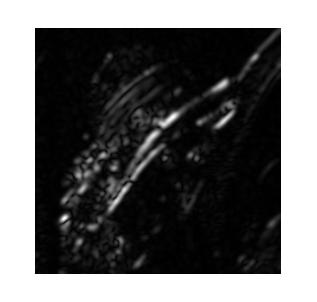
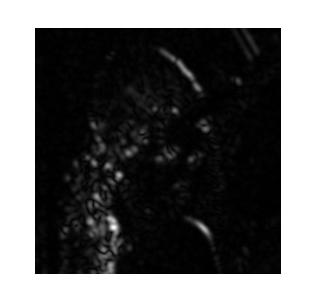
    利用一幅真實影像，按照文獻原文所說，利用4scales*6orientations的Gabor濾波器組進行紋理特徵提取，可以有效獲得影像紋理資訊。其中，單獨拿出某組相同scale的結果，展示如下所示。【別人的實驗結果，也沒給程式碼，我也沒去做】

好吧，今天寫到這裡，趕緊DOTA去了，有問題的一定要及時告訴我啊：）