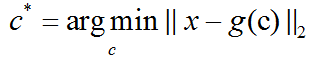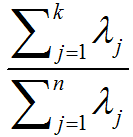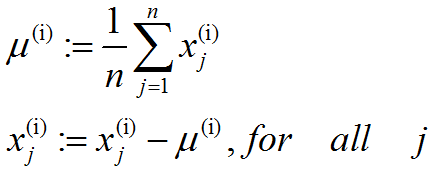主成分分析(PCA)簡介

主成分分析(Principal Components Analysis, PCA)是一個簡單的機器學習演算法，可以通過基礎的線性代數知識推導。

假設在Rⁿ空間中我們有m個點{x⁽¹⁾,…,x^(m)}，我們希望對這些點進行有失真壓縮。有失真壓縮表示我們使用更少的記憶體，但損失一些精度去儲存這些點。我們希望損失的精度儘可能少。

一種編碼這些點的方式是用低維表示。對於每個點x⁽ⁱ⁾∈Rⁿ,會有一個對應的編碼向量c⁽ⁱ⁾∈R^l。如果l比n小，那麼我們便使用了更少的記憶體來儲存原來的資料。我們希望找到一個編碼函式，根據輸入返回編碼，f(x)=c；我們也希望找到一個解碼函式，給定編碼重構輸入，x≈g(f(x)).

PCA由我們選擇的解碼函式而定。具體地，為了簡化解碼器，我們使用矩陣乘法將編碼對映回Rⁿ，即g(c)=Dc,其中D∈R^n*l是定義解碼的矩陣。

目前為止所描述的問題，可能會有多個解。因為如果我們按比例地縮小所有點對應的編碼向量c_i，那麼我們只需按比例放大D_:,i，即可保持結果不變。為了使問題有唯一解，我們限制D中所有列向量都有單位範數(unit norm)。

計算這個解碼器的最優編碼可能是一個困難的問題。為了使編碼問題簡單一些，PCA限制D的列向量彼此正交(注意，除非l=n，否則嚴格意義上D不是一個正交矩陣)。

為了將這個基本想法變為我們能夠實現的演算法，首先我們需要明確如果根據每一個輸入x得到一個最優編碼c^*。一種方法是最小化原始輸入向量x和重構向量g(c^*)之間的距離。我們使用範數來衡量它們之間的距離。在PCA演算法中，我們使用L²範數：

我們可以用平方L²範數替代L²範數，因為兩者在相同的值c上取得最小值。這是因為L2範數是非負的，並且平方運算在非負值上是單調遞增的。

主成分分析(PCA)：PCA演算法提供了一種壓縮資料的方式，也可以將PCA視為學習資料表示的無監督學習演算法。PCA學習一種比原始輸入維數更低的表示。它也學習了一種元素之間彼此沒有線性相關的表示。PCA可以通過協方差矩陣得到。主成分也可以通過奇異值分解(SVD)得到。

在多元統計分析中，PCA是一種分析、簡化資料集的技術。主成分分析經常用於減少資料集的維數，同時保持資料集中的對方差貢獻最大的特徵。這是通過保留低階主成分，忽略高階主成分做到的。這樣低階成分往往能夠保留住資料的最重要方面。但是，這也不是一定的，要視具體應用而定。由於主成分分析依賴所給資料，所以資料的準確性對分析結果影響很大。

主成分分析由卡爾•皮爾遜於1901年發明，用於分析資料及建立數理模型。其方法主要是通過對協方差矩陣進行特徵分解，以得出資料的主成分(即特徵向量)與它們的權值(即特徵值)。PCA是最簡單的以特徵量分析多元統計分佈的方法。其結果可以理解為對原資料中的方差做出解釋：哪一個方向上的資料值對方差影響最大？換而言之，PCA提供了一種降低資料維度的有效方法；如果分析者在原資料中除掉最小的特徵值所對應的成分，那麼所得的低維度資料必定是最優化的(也即，這樣降低維度必定是失去訊息最少的方法)。主成分分析在分析複雜資料時尤為有用，比如人臉識別。

PCA是最簡單的以特徵量分析多元統計分佈的方法。通常情況下，這種運算可以被看作是揭露資料的內部結構，從而更好的解釋資料的變數的方法。如果一個多後設資料集能夠在一個高維資料空間座標系中被顯現出來，那麼PCA就能夠提供一幅比較低維度的影像，這幅影像即為在訊息最多的點上原物件的一個”投影”。這樣就可以利用少量的主成分使得資料的維度降低了。

PCA的數學定義是：一個正交化線性變換，把資料變換到一個新的座標系統中，使得這一資料的任何投影的第一大方差在第一個座標(稱為第一主成分)上，第二大方差在第二個座標(第二主成分)上，依次類推。

定義一個n*m的矩陣，X^T為去平均值(以平均值為中心移動至原點)的資料，其行為資料樣本，列為資料類別(注意，這裡定義的是X^T而不是X)。則X的奇異值分解為X=WΣV^T,其中m*m矩陣W是XX^T的本徵向量矩陣，Σ是m*n的非負矩形對角矩陣，V是n*n的X^TX的本徵向量矩陣。據此，Y^T=X^TW=VΣ^TW^TW=VΣ^T,當m<n-1時，V在通常情況下不是唯一定義的，而Y則是唯一定義的。W是一個正交矩陣，Y^T是X^T的轉置，且Y^T的第一列由第一主成分組成，第二列由第二主成分組成，依次類推。

為了得到一種降低資料維度的有效辦法，我們可以利用W_L把X對映到一個只應用前面L個向量的低維空間中去：Y=W_L^TX=Σ_LV^T,其中Σ_L=I_L*mΣ,且I_L*m為L*m的單位矩陣。X的單向量矩陣W相當於協方差矩陣的本徵向量C=XX^T, XX^T=WΣΣ^TW^T.

在歐幾里得空間給定一組點數，第一主成分對應於通過多維空間平均點的一條線，同時保證各個點到這條直線距離的平方和最小。去除掉第一主成分後，用同樣的方法得到第二主成分。依次類推。在Σ中的奇異值均為矩陣XX^T的本徵值的平方根。每一個本徵值都與跟它們相關的方差是成正比的，而且所有本徵值的總和等於所有點到它們的多維空間平均點距離的平方和。PCA提供了一種降低維度的有效辦法，本質上，它利用正交變換將圍繞平均點的點集中儘可能多的變數投影到第一維中去，因此，降低維度必定是失去訊息最少的方法。PCA具有保持子空間擁有最大方差的最優正交變換的特性。然而，當與離散餘弦變換相比時，它需要更大的計算需求代價。非線性降維技術相對於PCA來說則需要更高的計算要求。

PCA對變數的縮放很敏感。如果我們只有兩個變數，而且它們具有相同的樣本方差，並且成正相關，那麼PCA將涉及兩個變數的主成分的旋轉。但是，如果把第一個變數的所有值都乘以100，那麼第一主成分就幾乎和這個變數一樣，另一個變數只提供了很小的貢獻，第二主成分也將和第二個原始變數幾乎一致。這就意味著當不同的變數代表不同的單位（如溫度和質量）時，PCA是一種比較武斷的分析方法。一種使PCA不那麼武斷的方法是使用變數縮放以得到單位方差。

通常，為了確保第一主成分描述的是最大方差的方向，我們會使用平均減法進行主成分分析。如果不執行平均減法，第一主成分有可能或多或少的對應於資料的平均值。另外，為了找到近似資料的最小均方誤差，我們必須選取一個零均值。

主成分分析的屬性和限制：主成分分析的結果取決於變數的縮放。主成分分析的適用性受到由它的派生物產生的某些假設的限制。

主成分分析和資訊理論：通過使用降維來儲存大部分資料資訊的主成分分析的觀點是不正確的。確實如此，當沒有任何假設資訊的訊號模型時，主成分分析在降維的同時並不能保證資訊的不丟失，其中資訊是由夏農熵來衡量的。基於假設得x=s+n也就是說，向量x是含有資訊的目標訊號s和噪聲訊號n之和，從資訊理論角度考慮主成分分析在降維上是最優的。

主成分分析(PCA)是一種能夠極大提升無監督特徵學習速度的資料降維演算法。更重要的是，理解PCA演算法，對實現白化演算法有很大的幫助，很多演算法都先用白化演算法作預處理步驟。假設你使用影像來訓練演算法，因為影像中相鄰的畫素高度相關，輸入資料是有一定冗餘的。具體來說，假如我們正在訓練的16*16灰度值影像，記為一個256維向量x∈R²⁵⁶，其中特徵值x_j對應每個畫素的亮度值。由於相鄰畫素間的相關性，PCA演算法可以將輸入向量轉換為一個維數低很多的近似向量，而且誤差非常小。

選擇主成分個數：決定k值時，我們通常會考慮不同k值可保留的方差百分比。具體來說，如果k=n，那麼我們得到的是對資料的完美近似，也就是保留了100%的方差，即原始資料的所有變化都被保留下來；相反，如果k=0，那等於是使用零向量來逼近輸入資料，也就是隻有0%的方差被保留下來。一般而言，設λ₁,λ₂,…,λ_n表示Σ的特徵值(按由大到小順序排列)，使得λ_j為對應於特徵向量u_j的特徵值。那麼如果我們保留前k個成分，則保留的方差百分比可計算為：

以處理影像資料為例，一個慣常的經驗法則是選擇k以保留99%的方差。對其它應用，如不介意引入稍大的誤差，有時也保留90-98%的方差範圍。

對影像資料應用PCA演算法：為使PCA演算法能有效工作，通常我們希望所有的特徵x₁,x₂,…,x_n都有相似的取值範圍(並且均值接近於0)。如果你曾在其它應用中使用過PCA演算法，你可能知道有必要單獨對每個特徵做預處理，即通過估算每個特徵x_j的均值和方差，而後將其取值範圍規整化為零均值和單位方差。但是，對於大部分影像型別，我們卻不需要進行這樣的預處理。假定我們將在自然影像上訓練演算法，此時特徵x_j代表的是畫素j的值。所謂”自然影像”，不嚴格的說，是指人或動物在他們一生中所見的那種影像。

注：通常我們選取含草木等內容的戶外場景圖片，然後從中隨機擷取小影像塊(如16*16畫素)來訓練演算法。在實踐中我們發現，大多數特徵學習演算法對訓練圖片的確切型別並不敏感，所以大多數用普通照相機拍攝的圖片，只要不是特別的模糊或帶有非常奇怪的人工痕跡，都可以使用。

在自然影像上進行訓練時，對每一個畫素單獨估計均值和方差意義不大，因為(理論上)影像任一部分的統計性質都應該和其它部分相同，影像的這種特性被稱作平穩性(stationarity)。

具體而言，為使PCA演算法正常工作，我們通常需要滿足以下要求：(1)、特徵的均值大致為0；(2)、不同特徵的方差值彼此相似。對於自然圖片，即使不進行方差歸一化操作，條件(2)也自然滿足，故而我們不再進行任何方差歸一化操作(對音訊資料,如聲譜,或文字資料,如詞袋向量，我們通常也不進行方差歸一化)。實際上，PCA演算法對輸入資料具有縮放不變性，無論輸入資料的值被如何放大(或縮小)，返回的特徵向量都不改變。更正式的說：如果將每個特徵向量x都乘以某個正數(即所有特徵量被放大或縮小相同的倍數)，PCA的輸出特徵向量都將不會發生變化。

既然我們不做方差歸一化，唯一還需進行的規整化操作就是均值規整化，其目的是保證所有特徵的均值都在0附近。根據應用，在大多數情況下，我們並不關注所輸入影像的整體明亮程度。比如在物件識別任務中，影像的整體明亮程度並不會影響影像中存在的是什麼物體。更為正式地說，我們對影像塊的平均亮度值不感興趣，所以可以減去這個值來進行均值規整化。具體的步驟是，如果x⁽ⁱ⁾∈Rⁿ代表16x16的影像塊的亮度(灰度)值(n=256)，可用如下演算法來對每幅影像進行零均值化操作：

 

請注意：(1)、對每個輸入影像塊x⁽ⁱ⁾都要單獨執行上面兩個步驟；(2)、這裡的μ⁽ⁱ⁾是指影像塊x⁽ⁱ⁾的平均亮度值。尤其需要注意的是，這和為每個畫素x_j單獨估算均值是兩個完全不同的概念。

如果你處理的影像並非自然影像(比如，手寫文字，或者白背景正中擺放單獨物體)，其他規整化操作就值得考慮了，而哪種做法最合適也取決於具體應用場合。但對自然影像而言，對每幅影像進行上述的零均值規整化，是預設而合理的處理。

以上內容主要摘自： 《深度學習中文版》、維基百科、UFLDL

GitHub： https://github.com/fengbingchun/NN_Test