再議gluPerspective和gluLookAt的關係

看了Opengl的相關程式，發現有些東西還是特別迷茫，尤其是gluLookAt的函式做啥用的，而gluPerspective又有什麼功能．

在網上檢視到了這篇：　終於搞明白gluPerspective和gluLookAt的關係了(zz)

http://cowboy.1988.blog.163.com/blog/static/751057982010101574732212/

我感覺它裡面沒有說清楚這些函式到底是做什麼用的，只是說了不同的引數有什麼效果．　我相信它做法是對的，但我更希望獲取why to do it? not just how to do it.

然後在網上又搜尋到了：　OpenGL入門學習[五]

http://apps.hi.baidu.com/share/detail/22508949

這篇比上面的稍微更加詳細點，但沒有系統的歸納，感覺有個斷層在上面．

從而不得已，再把先前的書(計算機圖形學--with opengl的描述）再翻了一遍前面部分．從而有了一個大概的思路．

也把我現在的困惑解開，我相信一些初學者也會從中得到啟發（如果能夠幫助您解惑，那就是我寫這篇blog的最大回報了）．

對於二維的圖形開發，拿簡單的圖片顯示來說，我們主要的目的：就是在一塊顯示ｂｕｆｆｅｒ中，不停的把每個畫素進行著色，然後就可以繪製出來了．為了速度，很多其他的加速方法，但原理基本上就是這樣了．　很直觀，也很簡單．　就像我們在畫布上進行著色，就可以了．

習慣了上面的二維的圖形開發，我們來到三維世界，感覺一下子找不到北了．　怎樣把顏色繪製上去了？怎樣旋轉／怎樣平移呢？等等問題都一一來了．

如果這時候，你去網上搜的話，有很多網頁都會提到只要呼叫某個函式就可了．(opengl裡面有現成的函式）

我們先不跳入到具體的函式裡面，而是把三維的影像繪製來整理一遍．

二維的影像顯示，我們感覺是在畫布上著色，而在三維的影像顯示，就相當於用照相機照相了．儘管最後底片上衝印出來的照片是二維的，但這個過程中就不再象我們二維那麼簡單的去著色了，它裡面有一個轉換的過程．如果我們知道了這個轉換過程，反過來來看相應的函式，就知道為什麼是這樣了．

座標系的區分我們就不提了，很多書上都寫過，也比較好理解．

一般來說，建模時採用建模座標系，然後在繪製的時候，先把建模座標系轉換到世界座標系．

opengl的座標系，　Ｚ的正方向指向螢幕外的（屬於右手座標系），Ｘ的正方向指向右，　Ｙ的正方向指向上．　

我們假設在前面某個點(0,10,-10)　放置了一個茶杯．　我們這樣把這個茶杯顯示在螢幕上呢？　如果是二維的開發，我們估計直接把茶杯的圖片顯示出來，而現在在三維上，我們是用相機來拍照，場景裡面就不只是一個茶杯了，還有其他的東西，並且茶杯如何體現它的三維的成像，也是一個問題．

既然是拍照，我們就需要把相機的位置調整好，這一般來說就是一個視點（看的地方）．　然後我們需要調整相機的朝向，這個也好理解．

剩下的問題是，我相機也選好位置了（0,10,0)，方向也選好了（指向(0,0,-1))． 好，這時我們要考慮一個初學者容易想不清楚的問題，茶杯如何在觀察螢幕顯示出來呢？

 

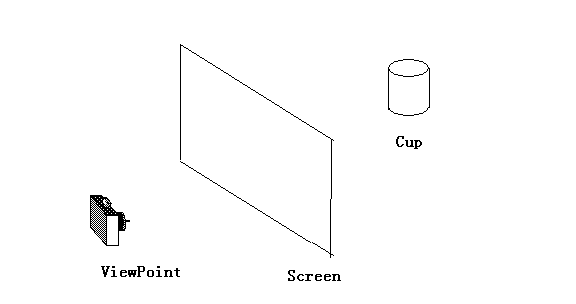
上面簡單的繪製了一個示意圖，為了把Cup繪製到Screen上，我們需要做下面的變換．

首先，我們建立一個觀察座標系，其原點在(ViewPoint)上，然後我們需要一個觀察平面（也就是上面的Screen,注意這個和真正螢幕顯示出來的有點差別，會有另外一個對應關係，不過也就是二維的變換，我們就不仔細區分）．　現在我們就想把Cup的形狀在觀察平面上投影，注意是投影．　這個投影的結果也就是我們繪製的結果．

既然是投影，就和座標有關聯了，因此我們必須把Cup都統一轉換到觀察座標系裡面來，這個過程涉及到平移／旋轉等操作．

當我們把Cup的座標和模型都使用了觀察座標系表示之後，　就要開始真正的投影了．

投影從數學角度來說，是比較簡單和直觀的．　正交投影和透視投影是兩種不同的投影．我在這邊把它比如成光源．正交投影，就是有一排平行於觀察平面的法線的方向的光源，它發出一組平行線，從而不管物體離觀察平面的遠近，大小都是一樣的．　

而透視投影，類似於有個點光源，它會發出一組相交於一點的光線，從而相同的大小，近的物體投影的大小大，而遠一些的就小一點．

投影之後，就在觀察介面有了顯示，這就是我們最終的成像了．　觀察平面從數學來說是無線大的，從我們實際使用角度，我們需要限制一個大小，這個大小也就決定了，我們那些區域可以顯示，其他投影在別的區域就忽略）．這就是很多書上說的裁剪視窗．

針對不同的投影，可以計算出每個點(x,y,z)在觀察平面的投影的位置(Xview, Yview, Zview).　問題就來了，不同的點有可能對映到相同的位置，怎樣來區分？？？　我發現前人真的很聰明，他們把這些投影的位置，他們引入了投影轉換的概念，使得先前物體的位置的ｚ保持不變，而把(x,y)轉換到(Xview,Yview)．這樣我們就發現，在前面的裁剪空間（人為的選定一個ｚ軸的near和far的區域），這個區域中就儲存了很多相同的點(Xview,Yview)只是z座標不同．　然後我們根據遠近的原則，就可以確定最終在觀察平面上的點是由那個空間點來決定的．　一般來說，為了統一化，經過投影轉換（也就是把x,y轉換成最終的對映到觀察平面的點(Xview,Yview)),我們就形成了一個統一的區域（這時就相當於正交投影了）．　因為這時每個點的ｘ，ｙ座標和最終對映到觀察平面是一致的．　這時統一之後，為了更加快捷操作，可以進一步做規範化處理（使得每個座標軸都在(-1,1)的範圍），然後進行區域裁剪，可見面的繪製，光照等著色處理．這樣就形成了最後的成像．　　

　　在正交投影時，就類似於我們在觀察平面上每個點(Xview,Yview)可以找到所對應的物體（根據ｚＢｕｆｆｅｒ來進行深度測試等）．這樣就能使得前面的物體可以擋住後面的物體．　最終就是通過投影變換，把不同的投影都轉換成最終的正交投影，然後感覺ｚ軸的不同進行深度測試，從而可以區分那些物體可以先畫，那些物體被遮擋．　統一了就好辦多了．:)

成像之後，我們在把成像的內容放到螢幕上去顯示（這有點類似於照片底片的沖印）．　我們觀察平面的裁剪視窗的大小和螢幕的大小可以一致，也可以有差別．　但為了使得最終的效果基本一致，所以，一般設定成它們具有相同的　aspect(橫縱比 w/h),　從而它們的轉換關係就是等比例的放大或者縮小，而不會產生扭曲．

上面這個過程，也就是我們三維顯示的過程．那怎樣和opengl來關聯呢？這就要呼叫opengl的相關函式了．

網上講解這些函式的很多，但和我們上面理解的過程如何對應起來的很少，很少．

首先：我們需要把顯示的物體轉換到觀察座標系

如果物體有自己的建模座標系，則需要把這個轉換到世界座標系，然後再轉換到觀察座標系．

既然座標系的轉換，那我們首先要建立觀察座標系．

因此，我們首先要選取觀察座標系的（原點，ｚ軸的，以及ｙ軸的方向），通過ｚ軸和ｙ軸的方向，可以確定ｘ軸的方向．

這個過程，opengl用

gluLookAt(GLdoble eyex,GLdouble eyey,GLdouble eyez,GLdouble centerx,GLdouble centery,GLdouble centerz,GLdouble upx,GLdouble upy,GLdouble upz);

函式來制定了，　它選取 eyex,eyey, eyez　做為原點（觀察座標系的座標（用世界座標系來表示的）），然後centerx, centery,centerz　指定了觀察方向（ｚ軸的反方向），　upx,upy,upz　指定了ｙ軸的正方向的近似方向（它不一定和ｚ軸方向正交，但可以通過相關的運算，找到正交的Ｙ軸的正方向，從而也可以找到ｘ軸的正方向．主要就是通過向量的點乘和叉乘來計算的））．

指定了這些，從而也就建立了從世界座標系到觀察座標系的轉換的矩陣．opengl的把這個轉換的矩陣儲存在矩陣堆疊中，從而後面就自動的把其他的世界座標系轉換到觀察座標系裡面）．　座標系的轉換，也就是物體的描述轉換到觀察座標系裡面了．從而後面的投影，就統一在觀察座標系裡面來計算．

這就是gluLookAt的函式的作用，它封裝了世界座標系到觀察座標系的轉換．　它在：glMatrixMode(GL_MODELVIEW);

的模式下呼叫的．

我們這樣來闡述了　gluLookAt的函式的原理和作用．現在應該清楚它是怎樣來的，為什麼來的吧？　說簡單就是為了建立座標系的轉換，把所有的物體都用觀察座標系來描述．　而不是從函式的名稱來看，感覺是讓我們看某個地方，儘管它有點這方面的含義，但不直觀．

ＯＫ，我們明白了gluLookAt的作用，呼叫之後，我們就把座標系變換的矩陣放入了矩陣棧，後續對物體的位置描述，會通過此矩陣棧進行轉換到我們的觀察座標系了．

從這點來說，還是很佩服opengl的設計者的思路，把變換矩陣進入了堆疊來儲存，從而在繪製不同的物體時，不需要把它當成額外的引數帶入．使得使用起來更加方便／直觀．　不過初學者，有些時候就感覺找不到北了，總感覺為何我們呼叫旋轉的函式，和物體有點不相關呢？

好，接下來，我們看看投影這塊．　既然，已經轉換到觀察座標系了，我們在觀察座標系的世界裡，把物體投影在我們的觀察平面的中，然後通過裁剪視窗，擷取我們需要的那塊就可以了．

我們這邊以：透視投影為例，　它是怎樣來達到這個效果呢？

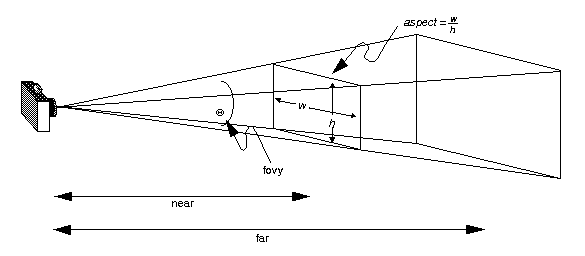
借用網上的這幅圖片，我們來說明gluPerspective,是做什麼的，為什麼要這麼做？

前面我們說過，透視投影，類似於一組聚焦的光線，把物體投影到我們的觀察平面上．

現在我們就在想，觀察平面在那呢？　投影的聚焦的光線聚焦在那點呢？

如果知道了這個，也就好算，某個位置的點在觀察平面上投影了．

Opengl規定，透視投影的聚焦點，在觀察座標系的原點（也就是我們gluLooKAt的指定的觀察點），那我們的觀察平面在哪呢？裁剪視窗又在哪呢？

這就是opengl裡面的gluPerspective要實現的．

gluPerspective(GLdouble fovy,GLdouble aspect,GLdouble zNear,GLdouble zFar)

zNear,zFar是到觀察原點的距離（沿著ｚ的負軸方向），因此這兩個數應該總數設定成正數．

從網上很多資料都在說，zNear和zFar做為一個深度的裁剪範圍，在這個範圍內的物體才能進行投影，否則就直接忽略．初學者到這個地方，也能夠理解，但從我們上面的問題來看，我們不知道觀察平面在哪呢？　其實opengl已經規定了，觀察平面就在近平面這裡，也就是zNear指定的地方，　觀察平面是平行於觀察座標系的（Ｘ，Ｙ），因此我們指定ｚ軸，也就指定它的位置．　

OK,我們的觀察平面已經確定了，那觀察平面的裁剪區域呢？

前面我們說過，觀察平面的裁剪視窗的　橫縱比（w/h)最好和螢幕的一致（估計說的不準確，也就是視口的橫縱比，從而只是等比例縮放而已）．　因此，gluPerspective的第二個引數就是 aspect了，這樣就把裁剪區域的寬度和高度的比例確定了．那剩下的是，我們目前還需要設定高度或者寬度．

gluPerspective的第一個引數是,fovy,它是一個角度．其實通過fovy和zNear能夠計算出裁剪視窗的高度．從而我們也就決定了裁剪視窗

的大小了．　fovy就是視錐體的上下平面的角度．　裁剪視窗的高度 h ＝ 2 * tan(fovy/2) * zNear.

從而我們也就明白了，上面有個網頁上，把它比如成眼睛的睜開度，感覺有點牽強．

從而我們知道，如果它為０的話，那肯定裁剪視窗的高度和寬度都為０，那就沒有任何顯示了．呵呵

如果它是１８０度，那就是裁剪視窗的高度就是無窮大，肯定沒有實際價值，程式有可能也崩潰了．

如果是178度，那它的裁剪視窗的高度也很大，裁剪的視窗越大，也就意味著它顯示的東西越多．　如果對於同一個物體成像來說，它在觀察平面的投影是不變的．　但由於底片的大小比我們視口的大，那我們就要等比例縮放了，從而在螢幕上的顯示時，我們就感覺它變小了．呵呵．

上面網頁上，還有一個截圖，如果設定成１度，在很遠的地方的一個球，感覺看的很大，很清楚，類似於照相機的鏡頭拉近了．

它也是一樣的原理，本身這個球，在１度還是９０度，在我們的觀察平面的投影是不變的，而變換的是我們的裁剪視窗的大小．設成１度，基本上裁剪視窗的高度很小，從而我們放到視口上，它就必須同比例的放大．從而就感覺放大了．並且顯示的場景的範圍也變小了．

好了，到目前位置，我們也就說清楚了gluLooKAt　和　gluPerspective的作用了，還有什麼不明白的，請評論？謝謝

視口的調整大小，opengl的函式是glViewPort，這個和二維的就一樣了，沒有特別需要注意的