【大創_社群劃分】——PageRank演算法的解析與Python實現

一、什麼是pagerank

PageRank的Page可是認為是網頁，表示網頁排名，也可以認為是Larry Page(google 產品經理)，因為他是這個演算法的發明者之一，還是google CEO（^_^）。PageRank演算法計算每一個網頁的PageRank值，然後根據這個值的大小對網頁的重要性進行排序。它的思想是模擬一個悠閒的上網者，上網者首先隨機選擇一個網頁開啟，然後在這個網頁上呆了幾分鐘後，跳轉到該網頁所指向的連結，這樣無所事事、漫無目的地在網頁上跳來跳去，PageRank就是估計這個悠閒的上網者分佈在各個網頁上的概率。

二、最簡單pagerank模型

網際網路中的網頁可以看出是一個有向圖，其中網頁是結點，如果網頁A有連結到網頁B，則存在一條有向邊A->B，下面是一個簡單的示例：

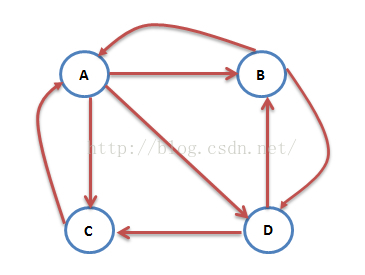
這個例子中只有四個網頁，如果當前在A網頁，那麼悠閒的上網者將會各以1/3的概率跳轉到B、C、D，這裡的3表示A有3條出鏈，如果一個網頁有k條出鏈，那麼跳轉任意一個出鏈上的概率是1/k，同理D到B、C的概率各為1/2，而B到C的概率為0。一般用轉移矩陣表示上網者的跳轉概率，如果用n表示網頁的數目，則轉移矩陣M是一個n*n的方陣；如果網頁j有k個出鏈，那麼對每一個出鏈指向的網頁i，有M[i][j]=1/k，而其他網頁的M[i][j]=0；上面示例圖對應的轉移矩陣如下：

初試時，假設上網者在每一個網頁的概率都是相等的，即1/n，於是初試的概率分佈就是一個所有值都為1/n的n維列向量V0，用V0去右乘轉移矩陣M，就得到了第一步之後上網者的概率分佈向量MV0,（nXn）*(nX1)依然得到一個nX1的矩陣。下面是V1的計算過程：

注意矩陣M中M[i][j]不為0表示用一個連結從j指向i，M的第一行乘以V0，表示累加所有網頁到網頁A的概率即得到9/24。得到了V1後，再用V1去右乘M得到V2，一直下去，最終V會收斂，即Vn=MV(n-1)，上面的圖示例，不斷的迭代，最終V=[3/9,2/9,2/9,2/9]‘：

三、終止點問題

上述上網者的行為是一個馬爾科夫過程的例項，要滿足收斂性，需要具備一個條件：

• 圖是強連通的，即從任意網頁可以到達其他任意網頁：

網際網路上的網頁不滿足強連通的特性，因為有一些網頁不指向任何網頁，如果按照上面的計算，上網者到達這樣的網頁後便走投無路、四顧茫然，導致前面累計得到的轉移概率被清零，這樣下去，最終的得到的概率分佈向量所有元素幾乎都為0。假設我們把上面圖中C到A的連結丟掉，C變成了一個終止點，得到下面這個圖：

對應的轉移矩陣為：

連續迭代下去，最終所有元素都為0：

四、陷阱問題

另外一個問題就是陷阱問題，即有些網頁不存在指向其他網頁的連結，但存在指向自己的連結。比如下面這個圖：

上網者跑到C網頁後，就像跳進了陷阱，陷入了漩渦，再也不能從C中出來，將最終導致概率分佈值全部轉移到C上來，這使得其他網頁的概率分佈值為0，從而整個網頁排名就失去了意義。如果按照上面圖對應的轉移矩陣為：

不斷的迭代下去，就變成了這樣：

五、解決終止點問題和陷阱問題

上面過程，我們忽略了一個問題，那就是上網者是一個悠閒的上網者，而不是一個愚蠢的上網者，我們的上網者是聰明而悠閒，他悠閒，漫無目的，總是隨機的選擇網頁，他聰明，在走到一個終結網頁或者一個陷阱網頁（比如兩個示例中的C），不會傻傻的乾著急，他會在瀏覽器的地址隨機輸入一個地址，當然這個地址可能又是原來的網頁，但這裡給了他一個逃離的機會，讓他離開這萬丈深淵。模擬聰明而又悠閒的上網者，對演算法進行改進，每一步，上網者可能都不想看當前網頁了，不看當前網頁也就不會點選上面的連線，而上悄悄地在位址列輸入另外一個地址，而在位址列輸入而跳轉到各個網頁的概率是1/n。假設上網者每一步檢視當前網頁的概率為a，那麼他從瀏覽器位址列跳轉的概率為(1-a)，於是原來的迭代公式轉化為：

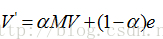
現在我們來計算帶陷阱的網頁圖的概率分佈：

重複迭代下去，得到：


六、用Python實現Page Rank演算法

from numpy import *

a = array([[0,1,1,0],
           [1,0,0,1],
           [1,0,0,1],
           [1,1,0,0]],dtype = float)  #dtype指定為float

def graphMove(a):   #構造轉移矩陣
    b = transpose(a)  #b為a的轉置矩陣
    c = zeros((a.shape),dtype = float)
    for i in range(a.shape[0]):
        for j in range(a.shape[1]):
            c[i][j] = a[i][j] / (b[j].sum())  #完成初始化分配
    #print c,"\n===================================================="
    return c

def firstPr(c):   #pr值得初始化
    pr = zeros((c.shape[0],1),dtype = float)  #構造一個存放pr值得矩陣
    for i in range(c.shape[0]):
        pr[i] = float(1)/c.shape[0]
    #print pr,"\n==================================================="
    return pr
    
def pageRank(p,m,v):  #計算pageRank值
    while((v == p*dot(m,v) + (1-p)*v).all()==False):  #判斷pr矩陣是否收斂,(v == p*dot(m,v) + (1-p)*v).all()判斷前後的pr矩陣是否相等，若相等則停止迴圈
        #print v
        v = p*dot(m,v) + (1-p)*v
        #print (v == p*dot(m,v) + (1-p)*v).all()
    return v

if __name__=="__main__":
    M = graphMove(a)
    pr = firstPr(M)
    p = 0.8           #引入瀏覽當前網頁的概率為p,假設p=0.8
    print pageRank(p,M,pr)  # 計算pr值