資料結構與演算法——優先佇列類的C++實現(二叉堆)

readyao發表於2016-04-14
資料結構演算法佇列C++

優先佇列簡介：

作業系統表明上看著是支援多個應用程式同時執行，事實上是每個時刻只能有一個程式執行，作業系統會排程不同的程式去執行。每個程式都只能執行一個固定的時間，當超過了該時間，作業系統就會暫停當前執行的程式，去排程其它程式來執行。

實現這種程式排程的一種方法是使用佇列。開始的時候程式被放在佇列的末尾，排程程式將反覆提取佇列中的第一個程式來執行，直到執行完畢或時間片用完，若程式沒有執行完畢則將該程式放入佇列的末尾。這種策略不是特別合適，因為可能一些短的程式需要等待很長的時間才能輪流到。一般來說，執行時間短的程式需要儘快的結束。所以那些執行時間短的程式需要比較高的優先權，同樣，那些比較重要的程式也需要比較高的優先權。
這種特殊的應用需要一種特殊的佇列-----優先佇列。可以用二叉堆實現優先佇列。

二叉堆簡介：

二叉堆與二叉查詢樹類似，二叉樹有兩個性質：結構性質和堆序性質。

結構性質：

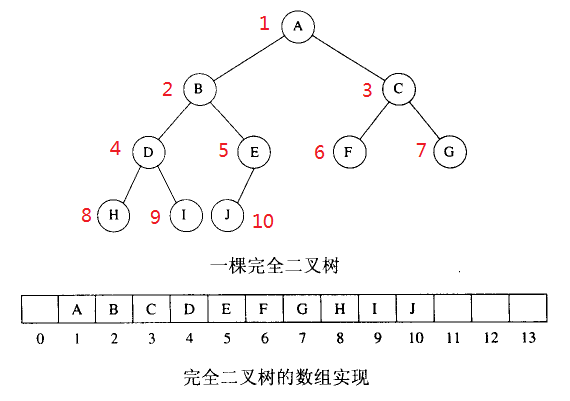
二叉堆是一棵完全二叉樹，除了子節點外的其它節點都有兩個兒子節點。
一棵高為h的完全二叉樹有2^h到2^(h+1) - 1個節點。完全二叉樹的高為log(N)，N為節點數目。
由於完全二叉樹的特點，實現起來很簡單，用簡單的陣列就可以實現。對於陣列中的任意位置i上的元素，其左兒子在位置2*i上，右兒子在(2*i)+1上，其父節點在i/2上（讓根節點在位置1）；


下面是一棵完全二叉樹的陣列實現圖示：



堆序性質：

因為如果想快速找到最小單元，則最小單元應該在根上。在堆中，對於每一個節點x,x的值大於等於子節點（葉子節點除外）；沒有二叉查詢樹的要求嚴格。

二叉堆的資料結構實現：

用一個陣列 vector<Comparable> v;來儲存所有的元素。
用currentSize來記錄當前元素的數目。
 

vector<Comparable> array;//儲存二叉堆的節點 
int currentSize;//當前二叉堆中的節點數目

二叉堆的主要成員函式：

bool isEmpty() const;//判斷二叉堆是否為空
const Comparable & findMin() const;//查詢最小元素

void insert(const Comparable & x);//插入元素x
void deleteMin();//刪除最小元素
void deleteMin(Comparable & minItem);//刪除最小元素，並以引用的方式返回該最小元素
void makeEmpty();//清空該二叉堆 
void print() const;//列印該堆元素

void buildHeap();//將元素移動到合適的位置
void percolateDown(int hole);//下移動

二叉堆的主要成員函式介紹：

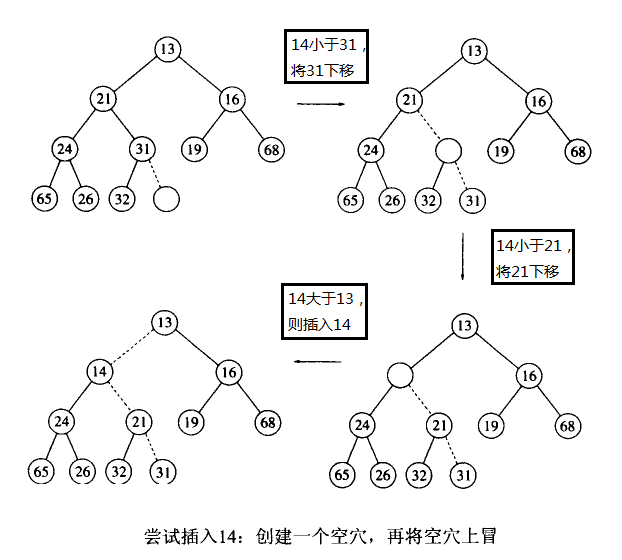
1、插入insert()：

比如：當插入14的時候，第一步在堆的下一個可用的位置建立空穴，如果在該空穴插入14後滿足堆序性，則插入成功。
但當在該空穴插入14之後不滿足堆序性，則將該空穴的父節點移入空穴，之前的父節點的位置變為了空穴。
然後再嘗試插入該新的空穴，如果不滿足堆序，則重複之前的操作。
 



/****************************************************************
*   函式名稱：insert(const Comparable & x)
*   功能描述: 刪除最小元素
*   引數列表: 無
*   返回結果：void 
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::insert(const Comparable & x)
{
    if(currentSize == array.size()-1)
        array.resize(2 * array.size());//擴大堆中陣列的容量

    //獲得空穴的位置
    int hole = ++currentSize;

    //上濾
    for(; hole > 1 && x < array[hole/2]; hole /= 2)
        array[hole] = array[hole/2];
    //將x插入到合適的位置
    array[hole] = x;
}

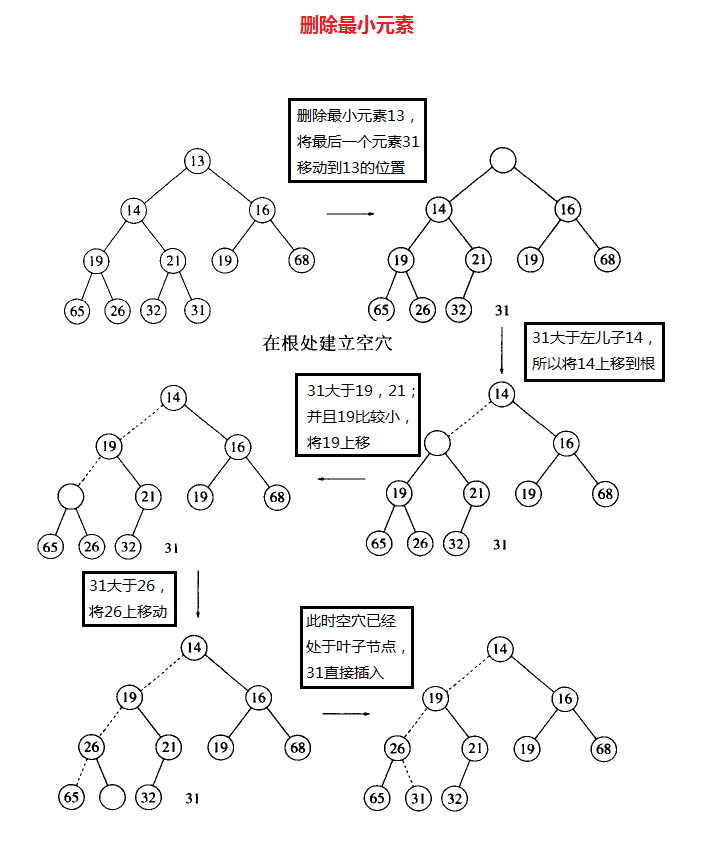
2、刪除最小元素deleteMin()：

將堆中最小的一個元素刪除之後（最下的元素位於堆陣列的最前面），必須將堆中最後一個元素x移動到堆中的某個合適的位置。.


比如:在下圖中刪除最小元素的操作。
刪除最小元素13，將最後一個元素31移動到13的位置；31比13的兩個孩子的值都大，所有將兩個孩子值比較小的上移動。所以將14上移動。然後31再和14的兩個孩子的值比較，直到31比空穴的兩個孩子的值都小，或者是空穴到了葉子節點，則直接將31插入到空穴。



/****************************************************************
*   函式名稱：deleteMin()
*   功能描述: 刪除最小元素
*   引數列表: 無
*   返回結果：void 
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::deleteMin()
{
    if(isEmpty()){
        cout << "BinaryHeap is empty." << endl;
        return;
    }

    array[1] = array[currentSize];//將最後一個元素移動到最小元素的位置
    currentSize--;//元素總數減去1
    //將最後一個元素移動到合適的位置
    percolateDown(1); 
}

/****************************************************************
*   函式名稱：percolateDown(int hole)
*   功能描述: 將array(hole)處的值向下移動 
*   引數列表: hole為堆中元素的位置標號
*   返回結果：void 
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::percolateDown(int hole)
{
    int child;
    //先儲存array[hole]的值
    Comparable temp = array[hole];

    for(; hole * 2 <= currentSize; hole = child){
        child = hole * 2;

        //child != currentSize,表明此時空穴有右兒子
        //array[child] > array[child+1] 表明此時空穴有右兒子小於左兒子
        if(child != currentSize && array[child] > array[child+1])
            child++;//此時child表示為空穴的右兒子

        //空穴的右兒子小於array[hole]
        if(array[child] < temp)
            array[hole] = array[child];
        else
            break;
    }

    array[hole] = temp;
}

下面是main函式，主要是對雜湊表類進行測試。


//測試主函式
int main()
{
    srand(unsigned(time(0)));
    BinaryHeap<int> binaryHeap;

    vector<int> v;

    for(int i = 0; i < 10; ++i)
        v.push_back(rand() % 10);
    cout << "v: ";
    for(int i = 0; i < 10; ++i)
        cout << v[i] << " ";
    cout << endl;
    

    for(int i = 0; i < 10; ++i)
        binaryHeap.insert(v[i]);

    binaryHeap.print();


    for(int i = 0; i < 12; i++){
        int minVal = 0;
        binaryHeap.deleteMin(minVal);
        cout << "刪除最小元素："  << minVal << endl;
        binaryHeap.print();
    }

    cout << "*****************************************" << endl;
    cout << "測試第二個建構函式: " << endl;
    BinaryHeap<int> binaryHeap2(v);
    binaryHeap2.print();

    for(int i = 0; i < 12; i++){
        int minVal = 0;
        binaryHeap2.deleteMin(minVal);
        cout << "刪除最小元素："  << minVal << endl;
        binaryHeap2.print();
    }


    return 0;
}

下面是二叉堆類的原始碼：

/*************************************************************************
	> File Name: binaryHeap.cpp
	> Author: 
	> Mail: 
	> Created Time: 2016年04月14日 星期四 11時37分43秒
 ************************************************************************/

#include <iostream>
#include <vector>
#include <time.h>
#include <stdlib.h>
using namespace std;



/******************************************
*   類的名稱：二叉堆
******************************************/

template<typename Comparable>
class BinaryHeap
{
    public:
        explicit BinaryHeap(int capacity = 100):array(capacity), currentSize(0){}
        explicit BinaryHeap(const vector<Comparable> & items);

        bool isEmpty() const;//判斷二叉堆是否為空
        const Comparable & findMin() const;//查詢最小元素
        
        void insert(const Comparable & x);//插入元素x
        void deleteMin();//刪除最小元素
        void deleteMin(Comparable & minItem);//刪除最小元素，並以引用的方式返回該最小元素
        void makeEmpty();//清空該二叉堆 
        void print() const;//列印該堆元素

    private:
        vector<Comparable> array;//儲存二叉堆的節點 
        int currentSize;//當前二叉堆中的節點數目
    private:
        void buildHeap();//將元素移動到合適的位置
        void percolateDown(int hole);//下移動
};

/****************************************************************
*   函式名稱：print() const
*   功能描述: 列印該堆元素 
*   引數列表: 無 
*   返回結果：無
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::print() const
{
    cout << "二叉堆的元素: " << endl;
    for(int i = 1; i <= currentSize; ++i)
        cout << array[i] << " ";
    cout << endl;
}

/****************************************************************
*   函式名稱：BinaryHeap(const vector<Comparable> & items)
*   功能描述: 建構函式
*   引數列表: items 是構造二叉堆需要的資料
*   返回結果：無
*****************************************************************/
template<typename Comparable>
BinaryHeap<Comparable>::BinaryHeap(const vector<Comparable> & items):array(items.size()+10), currentSize(items.size())
{
    for(unsigned i = 0; i < items.size(); ++i)
        array[i+1] = items[i];

    buildHeap();
}
/****************************************************************
*   函式名稱：buildHeap()
*   功能描述: 將元素移動到合適的位置，滿足堆序
*   引數列表: 無
*   返回結果：void
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::buildHeap()
{
    for(int i = currentSize / 2; i > 0; --i)
        percolateDown(i);
}

/****************************************************************
*   函式名稱：findMin()
*   功能描述: 查詢最小元素
*   引數列表: 無
*   返回結果：返回最小元素的引用
*****************************************************************/
template<typename Comparable>
const Comparable & BinaryHeap<Comparable>::findMin() const
{
   return array[1]; 
}

/****************************************************************
*   函式名稱：insert(const Comparable & x)
*   功能描述: 刪除最小元素
*   引數列表: 無
*   返回結果：void 
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::insert(const Comparable & x)
{
    if(currentSize == array.size()-1)
        array.resize(2 * array.size());//擴大堆中陣列的容量

    //獲得空穴的位置
    int hole = ++currentSize;

    //上濾
    for(; hole > 1 && x < array[hole/2]; hole /= 2)
        array[hole] = array[hole/2];
    //將x插入到合適的位置
    array[hole] = x;
}

/****************************************************************
*   函式名稱：deleteMin()
*   功能描述: 刪除最小元素
*   引數列表: 無
*   返回結果：void 
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::deleteMin()
{
    if(isEmpty()){
        cout << "BinaryHeap is empty." << endl;
        return;
    }

    array[1] = array[currentSize];//將最後一個元素移動到最小元素的位置
    currentSize--;//元素總數減去1
    //將最後一個元素移動到合適的位置
    percolateDown(1); 
}

/****************************************************************
*   函式名稱：percolateDown(int hole)
*   功能描述: 將array(hole)處的值向下移動 
*   引數列表: hole為堆中元素的位置標號
*   返回結果：void 
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::percolateDown(int hole)
{
    int child;
    //先儲存array[hole]的值
    Comparable temp = array[hole];

    for(; hole * 2 <= currentSize; hole = child){
        child = hole * 2;

        //child != currentSize,表明此時空穴有右兒子
        //array[child] > array[child+1] 表明此時空穴有右兒子小於左兒子
        if(child != currentSize && array[child] > array[child+1])
            child++;//此時child表示為空穴的右兒子

        //空穴的右兒子小於array[hole]
        if(array[child] < temp)
            array[hole] = array[child];
        else
            break;
    }

    array[hole] = temp;
}
/****************************************************************
*   函式名稱：deleteMin(Comparable & minItem)
*   功能描述: 刪除最小元素
*   引數列表: minItem 將最小元素賦值給引用minItem
*   返回結果：void 
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::deleteMin(Comparable & minItem)
{
    if(isEmpty()){
        cout << "binaryHeap is empty." << endl;
        return;
    }

    minItem = array[1];

    array[1] = array[currentSize--];
    percolateDown(1);
}

/****************************************************************
*   函式名稱：makeEmpty()
*   功能描述: 情況二叉堆
*   引數列表: 無
*   返回結果：void 
*****************************************************************/
template<typename Comparable>
void BinaryHeap<Comparable>::makeEmpty()
{
    currentSize = 0;
}

/****************************************************************
*   函式名稱：isEmpty()
*   功能描述: 判斷二叉堆是否為空
*   引數列表: 無
*   返回結果：如果為空，則返回true，否則返回false
*****************************************************************/
template<typename Comparable>
bool BinaryHeap<Comparable>::isEmpty() const
{
    return currentSize == 0;
}




//測試主函式
int main()
{
    srand(unsigned(time(0)));
    BinaryHeap<int> binaryHeap;

    vector<int> v;

    for(int i = 0; i < 10; ++i)
        v.push_back(rand() % 10);
    cout << "v: ";
    for(int i = 0; i < 10; ++i)
        cout << v[i] << " ";
    cout << endl;
    

    for(int i = 0; i < 10; ++i)
        binaryHeap.insert(v[i]);

    binaryHeap.print();


    for(int i = 0; i < 12; i++){
        int minVal = 0;
        binaryHeap.deleteMin(minVal);
        cout << "刪除最小元素："  << minVal << endl;
        binaryHeap.print();
    }

    cout << "*****************************************" << endl;
    cout << "測試第二個建構函式: " << endl;
    BinaryHeap<int> binaryHeap2(v);
    binaryHeap2.print();

    for(int i = 0; i < 12; i++){
        int minVal = 0;
        binaryHeap2.deleteMin(minVal);
        cout << "刪除最小元素："  << minVal << endl;
        binaryHeap2.print();
    }


    return 0;
}

下面是程式的執行結果：

v: 5 3 8 4 3 6 1 5 4 5 
二叉堆的元素: 
1 3 3 4 4 8 6 5 5 5 
刪除最小元素：1
二叉堆的元素: 
3 4 3 5 4 8 6 5 5 
刪除最小元素：3
二叉堆的元素: 
3 4 5 5 4 8 6 5 
刪除最小元素：3
二叉堆的元素: 
4 4 5 5 5 8 6 
刪除最小元素：4
二叉堆的元素: 
4 5 5 6 5 8 
刪除最小元素：4
二叉堆的元素: 
5 5 5 6 8 
刪除最小元素：5
二叉堆的元素: 
5 6 5 8 
刪除最小元素：5
二叉堆的元素: 
5 6 8 
刪除最小元素：5
二叉堆的元素: 
6 8 
刪除最小元素：6
二叉堆的元素: 
8 
刪除最小元素：8
二叉堆的元素: 

binaryHeap is empty.
刪除最小元素：0
二叉堆的元素: 

binaryHeap is empty.
刪除最小元素：0
二叉堆的元素: 

*****************************************
測試第二個建構函式: 
二叉堆的元素: 
1 3 5 4 3 6 8 5 4 5 
刪除最小元素：1
二叉堆的元素: 
3 3 5 4 5 6 8 5 4 
刪除最小元素：3
二叉堆的元素: 
3 4 5 4 5 6 8 5 
刪除最小元素：3
二叉堆的元素: 
4 4 5 5 5 6 8 
刪除最小元素：4
二叉堆的元素: 
4 5 5 8 5 6 
刪除最小元素：4
二叉堆的元素: 
5 5 5 8 6 
刪除最小元素：5
二叉堆的元素: 
5 6 5 8 
刪除最小元素：5
二叉堆的元素: 
5 6 8 
刪除最小元素：5
二叉堆的元素: 
6 8 
刪除最小元素：6
二叉堆的元素: 
8 
刪除最小元素：8
二叉堆的元素: 

binaryHeap is empty.
刪除最小元素：0
二叉堆的元素: 

binaryHeap is empty.
刪除最小元素：0
二叉堆的元素:

相關文章