資料結構與演算法——二叉查詢樹類的C++實現
二叉樹的平均深度為O(logN);
二叉查詢樹在二叉樹的基礎上,增加的性質為:對於樹中每一個結點X,它的左子樹中所有項的值小於X中的項,而它的右子樹中所有項的值大於X中的項。
該二叉查詢樹結點的資料結構:
struct BinaryNode{
Comparable element;//結點的值
BinaryNode * left;//結點的左孩子
BinaryNode * right;//結點的右孩子
int num;//相同值的結點出現的次數,如果不考慮重複元素的話,該成員可以省去
BinaryNode(const Comparable & e, BinaryNode* lt, BinaryNode* rt, int n):element(e), left(lt), right(rt), num(n){}
};該結點資料結構其實是一個結點類。
該二叉查詢樹的主要成員函式:
BinarySearchTree(){root = NULL;}//建構函式
BinarySearchTree(vector<int> & v);//建構函式
BinarySearchTree(const BinarySearchTree & rhs);//複製建構函式
const BinarySearchTree & operator=(const BinarySearchTree & rhs);//賦值運算子過載
~BinarySearchTree();//解構函式
void preOrderPrintTree() const;//從小到大列印該二叉查詢樹
void inOrderPrintTree() const;//從大到小列印該二叉查詢樹
Comparable findMin() const;//查詢最小值
Comparable findMax() const;//查詢最大值
bool contains(const Comparable & x) const;//判斷該二叉查詢樹是否包含值為x的結點
bool isEmpty() const;//判斷該二叉查詢樹是否為空
void makeEmpty();//清空該二叉查詢樹
void insert(const Comparable & x);//插入結點
void remove(const Comparable & x);//移除結點值為x的結點主要成員函式介紹:
void remove(const Comparable & x);//移除結點值為x的結點
/****************************************************************
* 函式名稱:remove(const Comparable & x)
* 功能描述: 移除結點
* 引數列表: x -- 要移除的結點的值
* 返回結果:void
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::remove(const Comparable & x)
{
remove(x, root);
}
template<typename Comparable>
void BinarySearchTree<Comparable>::remove(const Comparable & x, BinaryNode * &t) const
{
if(t == NULL)
return;
if(x < t->element)
remove(x, t->left);
else if(x > t->element)
remove(x, t->right);
else if((t->left != NULL) && (t->right != NULL)){//該結點有兩個兒子的時候,將該結點右子樹的最小結點覆蓋該結點的值,然後再刪除那個最小結點
t->element = findMin(t->right);
remove(t->element, t->right);
}
else {//該結點只有一個兒子的時候,將兒子放在當前結點的位置。用另一個指標儲存當前結點,然後刪除該結點;此時也包括該結點為葉子結點的情況
BinaryNode * oldCurrentNode = t;
t = (t->left == NULL) ? t->right : t->left;
delete oldCurrentNode;
}
}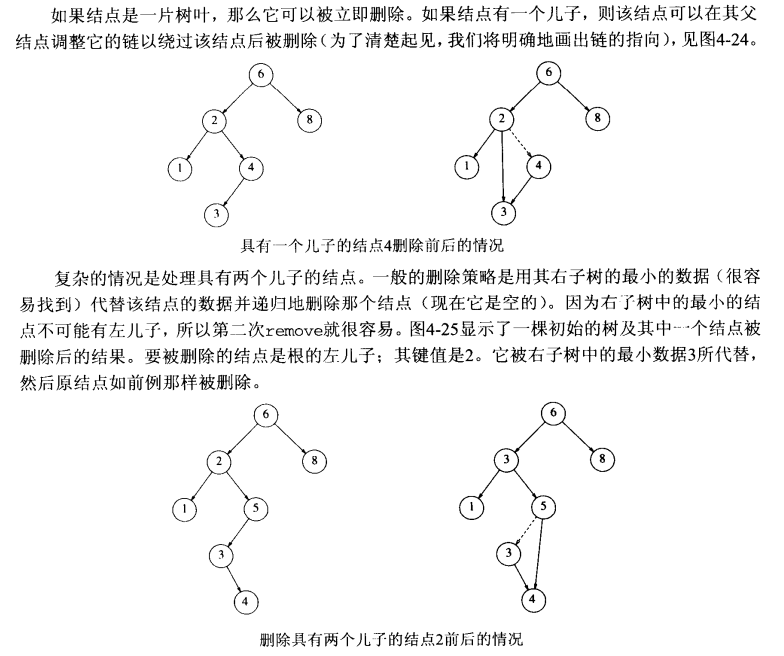
下面的main函式是對remove成員函式的測試,用的就是上面兩個圖:
int main()
{
BinarySearchTree<int> tree;
tree.insert(6);
tree.insert(2);
tree.insert(1);
tree.insert(4);
tree.insert(3);
tree.insert(8);
tree.preOrderPrintTree();
tree.remove(4);
tree.preOrderPrintTree();
BinarySearchTree<int> tree2;
tree2.insert(6);
tree2.insert(2);
tree2.insert(1);
tree2.insert(5);
tree2.insert(3);
tree2.insert(4);
tree2.insert(8);
tree2.preOrderPrintTree();
tree2.remove(2);
tree2.preOrderPrintTree();
return 0;
}下面是該二叉查詢樹類的原始碼:
/*************************************************************************
> File Name: BinarySearchTree.cpp
> Author:
> Mail:
> Created Time: 2016年04月06日 星期三 17時19分47秒
************************************************************************/
#include <iostream>
#include <vector>
#include <stdlib.h>
#include <time.h>
using namespace std;
template<typename Comparable>
class BinarySearchTree{
public:
BinarySearchTree(){root = NULL;}
BinarySearchTree(vector<int> & v);
BinarySearchTree(const BinarySearchTree & rhs);
~BinarySearchTree();
const BinarySearchTree & operator=(const BinarySearchTree & rhs);//賦值運算子過載
void preOrderPrintTree() const;//從小到大列印該二叉查詢樹
void inOrderPrintTree() const;//從大到小列印該二叉查詢樹
Comparable findMin() const;//查詢最小值
Comparable findMax() const;//查詢最大值
bool contains(const Comparable & x) const;//判斷該二叉查詢樹是否包含值為x的結點
void makeEmpty();//清空該二叉查詢樹
bool isEmpty() const;//判斷該二叉查詢樹是否為空
void insert(const Comparable & x);//插入結點
void remove(const Comparable & x);//移除結點值為x的結點
private:
//樹結點的資料結構
struct BinaryNode{
Comparable element;
BinaryNode * left;
BinaryNode * right;
int num;//相同值的結點出現的次數
BinaryNode(const Comparable & e, BinaryNode* lt, BinaryNode* rt, int n):element(e), left(lt), right(rt), num(n){}
};
BinaryNode* root;
void insert(const Comparable & x, BinaryNode * &t) const;
void remove(const Comparable & x, BinaryNode * &t) const;
void preOrder(BinaryNode * t) const;//前序遍歷
void inOrder(BinaryNode * t) const;//中序遍歷
void deleteNode(BinaryNode * t);//釋放結點t
Comparable &findMin(BinaryNode * node) const;
Comparable &findMax(BinaryNode * node) const;
bool contains(const Comparable & x, BinaryNode * t) const;//判斷該二叉查詢樹是否包含值為x的結點
BinaryNode *clone(BinaryNode * t) const{
if(t == NULL)
return NULL;
return new BinaryNode(t->element, clone(t->left), clone(t->right), t->num);
}
};
/****************************************************************
* 函式名稱:BinarySearchTree(const BinarySearchTree & rhs)
* 功能描述: 該二叉查詢樹的複製建構函式
* 引數列表: rhs 要複製的二叉查詢樹
* 返回結果:無
*****************************************************************/
template<typename Comparable>
BinarySearchTree<Comparable>::BinarySearchTree(const BinarySearchTree & rhs)
{
root = clone(rhs.root);
}
/****************************************************************
* 函式名稱:BinarySearchTree(const BinarySearchTree & rhs)
* 功能描述: 該二叉查詢樹的複製建構函式
* 引數列表: rhs 要複製的二叉查詢樹
* 返回結果:無
*****************************************************************/
template<typename Comparable>
const BinarySearchTree<Comparable> & BinarySearchTree<Comparable>::operator=(const BinarySearchTree & rhs)//賦值運算子過載
{
if(this != &rhs){
makeEmpty();
root = clone(rhs.root);
}
return *this;
}
/****************************************************************
* 函式名稱:contains(const Comparable & x)const
* 功能描述: 判斷該二叉查詢樹是否含有值為x的結點
* 引數列表: 無
* 返回結果:如果有值為x的結點,則返回true;
* 如果沒有值為x的結點,則返回false;
*****************************************************************/
template<typename Comparable>
bool BinarySearchTree<Comparable>::contains(const Comparable & x) const
{
if(isEmpty())
return false;
else
return contains(x, root);
}
template<typename Comparable>
bool BinarySearchTree<Comparable>::contains(const Comparable & x, BinaryNode * t) const
{
if(t == NULL)
return false;
if(x == t->element)
return true;
else if(x > t->element)
return contains(x, t->right);
else if(x < t->element)
return contains(x, t->left);
}
/****************************************************************
* 函式名稱:findMax()const
* 功能描述: 查詢樹的最大值
* 引數列表: 無
* 返回結果:結點值的引用
*****************************************************************/
template<typename Comparable>
Comparable BinarySearchTree<Comparable>::findMax() const
{
if(!isEmpty())
return findMax(root);
}
/****************************************************************
* 函式名稱:findMax(BinaryNode *node)const
* 功能描述: 查詢樹的最大值
* 引數列表: 無
* 返回結果:結點值的引用
*****************************************************************/
template<typename Comparable>
Comparable & BinarySearchTree<Comparable>::findMax(BinaryNode * node) const
{
if(node->right== NULL)
return node->element;
else
return findMax(node->right);
}
/****************************************************************
* 函式名稱:findMin()const
* 功能描述: 查詢樹的最小值
* 引數列表: 無
* 返回結果:結點值的引用
*****************************************************************/
template<typename Comparable>
Comparable BinarySearchTree<Comparable>::findMin() const
{
if(!isEmpty())
return findMin(root);
}
/****************************************************************
* 函式名稱:findMin(BinaryNode *node)const
* 功能描述: 查詢樹的最小值
* 引數列表: 無
* 返回結果:結點值的引用
*****************************************************************/
template<typename Comparable>
Comparable & BinarySearchTree<Comparable>::findMin(BinaryNode * node) const
{
if(node->left == NULL)
return node->element;
else
return findMin(node->left);
}
/****************************************************************
* 函式名稱:BinarySearchTree(vector<int> &)
* 功能描述: 建構函式
* 引數列表: v 用於構造二叉查詢樹的資料序列
* 返回結果:無
*****************************************************************/
template<typename Comparable>
BinarySearchTree<Comparable>::BinarySearchTree(vector<int> & v)
{
root = NULL;//必須初始化,否則析構的時候會出錯
for(vector<int>::iterator it = v.begin(); it != v.end(); ++it)
insert(*it);
}
/****************************************************************
* 函式名稱:~BinarySearchTree()
* 功能描述: 解構函式
* 引數列表: 無
* 返回結果:無
*****************************************************************/
template<typename Comparable>
BinarySearchTree<Comparable>::~BinarySearchTree()
{
//deleteNode(root);
makeEmpty();//兩種方式都可以
}
/****************************************************************
* 函式名稱:deleteNode(BinaryNode *t)
* 功能描述: 釋放結點
* 引數列表: 要釋放結點的指標
* 返回結果:void
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::deleteNode(BinaryNode * t)
{
//後序遍歷的方式釋放所有結點
if(t != NULL){
deleteNode(t->left);
deleteNode(t->right);
//cout << "t->element = " << t->element << endl;
delete t;
}
}
/****************************************************************
* 函式名稱:isEmpty() const
* 功能描述: 判斷該二叉查詢樹是否為空
* 引數列表: 無
* 返回結果:如果該樹為空,則返回true;
* 如果該樹為不為空,則返回false
*****************************************************************/
template<typename Comparable>
bool BinarySearchTree<Comparable>::isEmpty()const
{
return (root == NULL) ? true : false;
}
/****************************************************************
* 函式名稱:makeEmpty()
* 功能描述: 將該二叉查詢樹清空
* 引數列表: 無
* 返回結果:無
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::makeEmpty()
{
deleteNode(root);//移除所有結點
root = NULL;
}
/****************************************************************
* 函式名稱:preOrderPrintTree() const
* 功能描述: 按從小到大的順序輸出該二叉查詢樹
* 引數列表: 無
* 返回結果:void
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::preOrderPrintTree() const
{
cout << "按從小到大的順序輸出該二叉查詢樹: ";
preOrder(root);
cout << endl;
}
/****************************************************************
* 函式名稱:preOrder(BinaryNode * t) const
* 功能描述: 按從小到大的順序輸出該二叉查詢樹,前序遍歷
* 引數列表: 當前結點的指標
* 返回結果:void
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::preOrder(BinaryNode * t) const
{
if(t != NULL){
preOrder(t->left);//列印左子樹
for(int i = 0; i < t->num; ++i)
cout << t->element << " ";//列印父結點,可能有多個值
preOrder(t->right);//列印右子樹
}
}
/****************************************************************
* 函式名稱:inOrderPrintTree() const
* 功能描述: 按從大到小的順序列印該二叉樹
* 引數列表: 無
* 返回結果:void
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::inOrderPrintTree() const
{
cout << "按從大到小的順序輸出該二叉查詢樹: ";
inOrder(root);
cout << endl;
}
/****************************************************************
* 函式名稱:inOrder(BinaryNode * t) const
* 功能描述: 按從小到大的順序輸出該二叉查詢樹,前序遍歷
* 引數列表: 當前結點的指標
* 返回結果:void
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::inOrder(BinaryNode * t) const
{
if(t != NULL){
inOrder(t->right);//列印右子樹
for(int i = 0; i < t->num; ++i)
cout << t->element << " ";//列印父結點,可能有多個值
inOrder(t->left);//列印左子樹
}
}
/****************************************************************
* 函式名稱:remove(const Comparable & x)
* 功能描述: 移除結點
* 引數列表: x -- 要移除的結點的值
* 返回結果:void
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::remove(const Comparable & x)
{
remove(x, root);
}
template<typename Comparable>
void BinarySearchTree<Comparable>::remove(const Comparable & x, BinaryNode * &t) const
{
if(t == NULL)
return;
if(x < t->element)
remove(x, t->left);
else if(x > t->element)
remove(x, t->right);
else if((t->left != NULL) && (t->right != NULL)){//該結點有兩個兒子的時候,將該結點右子樹的最小結點覆蓋該結點的值,然後再刪除那個最小結點
t->element = findMin(t->right);
remove(t->element, t->right);
}
else {//該結點只有一個兒子的時候,將兒子放在當前結點的位置。用另一個指標儲存當前結點,然後刪除該結點
BinaryNode * oldCurrentNode = t;
t = (t->left == NULL) ? t->right : t->left;
delete oldCurrentNode;
}
}
/****************************************************************
* 函式名稱:insert(const Comparable & x)
* 功能描述: 插入值為x的結點
* 引數列表: x 要插入的值
* 返回結果:void
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::insert(const Comparable & x)
{
insert(x, root);
}
/****************************************************************
* 函式名稱:insert(const Comparable & x, BinaryNode * & t) const
* 功能描述: 在結點t上插入值為x的結點
* 引數列表: x 要插入的值
* t 要插入到結點t上
* 返回結果:void
*****************************************************************/
template<typename Comparable>
void BinarySearchTree<Comparable>::insert(const Comparable & x, BinaryNode * & t) const
{
if(t == NULL)
t = new BinaryNode(x, NULL, NULL, 1);
else if(x > t->element)
insert(x, t->right);
else if(x < t->element)
insert(x, t->left);
else if(x == t->element)//如果要插入的值和當前結點的值相同,則將當前結點的個數加1
t->num++;
}
//測試該二叉查詢樹的成員函式
int main0()
{
// srand(unsigned (time(0)));
vector<int> v;
//隨機生成一個資料序列
for(int i = 0; i < 10; ++i)
v.push_back(rand()%10);
cout << "隨機產生的資料序列: ";
for(vector<int>::iterator it = v.begin(); it != v.end(); ++it)
cout << *it << " ";
cout << endl;
//用第一個建構函式生成該二叉查詢樹
BinarySearchTree<int> tree;
if(tree.isEmpty())
cout << "該樹此時為空." << endl;
else
cout << "該樹此時為不為空." << endl;
for(vector<int>::iterator it = v.begin(); it != v.end(); ++it)
tree.insert(*it);
if(tree.isEmpty())
cout << "該樹此時為空." << endl;
else
cout << "該樹此時為不為空." << endl;
cout << "tree1: " << endl;
tree.preOrderPrintTree();//從小到大輸出該二叉查詢樹
tree.inOrderPrintTree();//從大到小輸出該二叉查詢樹
int min = tree.findMin();
cout << "min = " << min << endl;
int max = tree.findMax();
cout << "max = " << max << endl;
if(tree.contains(5))
cout << "contains(5))" << endl;
else
cout << "not contains(5)" << endl;
BinarySearchTree<int> tree3 = tree;
tree3.preOrderPrintTree();
tree3.inOrderPrintTree();
BinarySearchTree<int> tree4;
tree4 = tree;
tree4.preOrderPrintTree();
tree4.inOrderPrintTree();
/*
tree.makeEmpty();
if(tree.isEmpty())
cout << "該樹此時為空." << endl;
else
cout << "該樹此時為不為空." << endl;
*/
//用第二個建構函式生成該二叉查詢樹
cout << "tree2: " << endl;
BinarySearchTree<int> tree2(v);
tree2.preOrderPrintTree();//從小到大輸出該二叉查詢樹
tree2.inOrderPrintTree();//從大到小輸出該二叉查詢樹
return 0;
}
//test the functiona of remove
int main()
{
BinarySearchTree<int> tree;
tree.insert(6);
tree.insert(2);
tree.insert(1);
tree.insert(4);
tree.insert(3);
tree.insert(8);
tree.preOrderPrintTree();
tree.remove(4);
tree.preOrderPrintTree();
BinarySearchTree<int> tree2;
tree2.insert(6);
tree2.insert(2);
tree2.insert(1);
tree2.insert(5);
tree2.insert(3);
tree2.insert(4);
tree2.insert(8);
tree2.preOrderPrintTree();
tree2.remove(2);
tree2.preOrderPrintTree();
return 0;
}
相關文章
- 資料結構與演算法——表示式樹類的C++實現(二叉樹)資料結構演算法C++二叉樹
- 資料結構與演算法-二叉查詢樹資料結構演算法
- 『資料結構與演算法』二叉查詢樹(BST)資料結構演算法
- 資料結構與演算法——AVL樹類的C++實現資料結構演算法C++
- 資料結構與演算法-二叉查詢樹平衡(DSW)資料結構演算法
- 資料結構與演算法-二叉查詢樹平衡(AVL)資料結構演算法
- 【資料結構與演算法】手撕二叉查詢樹資料結構演算法
- 二叉查詢樹的實現——C++C++
- 資料結構與演算法——B樹的C++實現資料結構演算法C++
- 資料結構與演算法——單詞查詢樹資料結構演算法
- 二叉樹 & 二叉查詢樹 ADT【資料結構與演算法分析 c 語言描述】二叉樹資料結構演算法
- 二叉樹 & 二叉查詢樹 ADT [資料結構與演算法分析 c 語言描述]二叉樹資料結構演算法
- JS中的演算法與資料結構——二叉查詢樹(Binary Sort Tree)JS演算法資料結構
- 資料結構與演算法——優先佇列類的C++實現(二叉堆)資料結構演算法佇列C++
- 淺談演算法和資料結構(7):二叉查詢樹演算法資料結構
- 資料結構與演算法——普通樹的定義與C++實現資料結構演算法C++
- 資料結構:二叉查詢樹的相關操作資料結構
- 【資料結構與演算法】二叉樹資料結構演算法二叉樹
- 【資料結構】二叉樹(c++)資料結構二叉樹C++
- 資料結構與演算法——不相交集類的C++實現資料結構演算法C++
- 資料結構與演算法:二叉排序樹資料結構演算法排序
- javascript資料結構與演算法-- 二叉樹JavaScript資料結構演算法二叉樹
- 資料結構與演算法知識點總結(5)查詢樹資料結構演算法
- 二叉查詢樹【二叉排序樹】構建和查詢演算法 PHP 版排序演算法PHP
- 【演算法資料結構Java實現】折半查詢演算法資料結構Java
- 資料結構-二叉搜尋樹的實現資料結構
- 【演算法與資料結構 02】二叉樹的引入演算法資料結構二叉樹
- 【資料結構與演算法】二叉排序樹C實現(含完整原始碼)資料結構演算法排序原始碼
- 資料結構與演算法-kd二叉樹(kNN)資料結構演算法二叉樹KNN
- 資料結構與演算法-表示式二叉樹資料結構演算法二叉樹
- 資料結構與演算法-二叉樹性質資料結構演算法二叉樹
- 資料結構與演算法-二叉樹遍歷資料結構演算法二叉樹
- C++二叉查詢樹實現過程詳解C++
- 資料結構和演算法-Go實現二叉搜尋樹資料結構演算法Go
- 資料結構——樹與二叉樹的遍歷資料結構二叉樹
- 資料結構與演算法:查詢演算法資料結構演算法
- 轉:C++實現的變種二分查詢法(折半查詢)--二叉查詢樹C++
- python資料結構之二叉樹的實現Python資料結構二叉樹