資料結構與演算法——RB樹簡介

readyao發表於2016-03-28
資料結構演算法

二叉樹：

任何節點最多隻允許有兩個子節點。

二叉搜尋樹：

可以提供對數時間的元素插入和訪問。任何節點的鍵值一定大於其左子樹中的每一個節點的鍵值，並不小於其右子樹中的每一個節點的鍵值。

平衡二叉搜尋樹：

平衡的意思是，沒有任何一個節點過深（深度過大）。二叉搜尋樹可能會在多次插入或刪除之後，變得不平衡。

AVL-tree、RB-tree和AA-tree均可實現出平衡二叉搜尋樹。RB-tree的搜尋效率和AVL-tree幾乎相等。


RB-Tree（紅黑樹）:

標準的STL關聯式容器分為set(集合)和map(對映表)兩大類。以及這兩者的衍生體multiset(多鍵集合)和multimap(多鍵對映表)；
這些容器的底層機制都是以RB-Tree（紅黑樹）完成。
在關聯式容器中，每個元素都有一個鍵值（key）和值（value）。當元素插入到該容器的時候，容器內部結構（比如：紅黑樹，或hash-table）便依照該元素鍵值的大小，以某種特定的規則將該元素插入到容器的特定的位置。


RB-Tree（紅黑樹）的特點:

RB-tree除了是一個二叉搜尋樹之外，還滿足下面規則：

1.每個節點不是紅色就是黑色。

2.根節點為黑色。

3.如果節點為紅色，其子節點必須為黑。

4.任一節點到NULL(樹尾部，即樹葉)的任何路徑，所含黑節點數必須相同。


根據規則4，新增節點必須為紅色。
根據規則3，新增節點的父節點必須為黑。（因為新增節點是紅色，紅色節點只能有黑節點兒子，所以新增節點的父節點必須為黑）

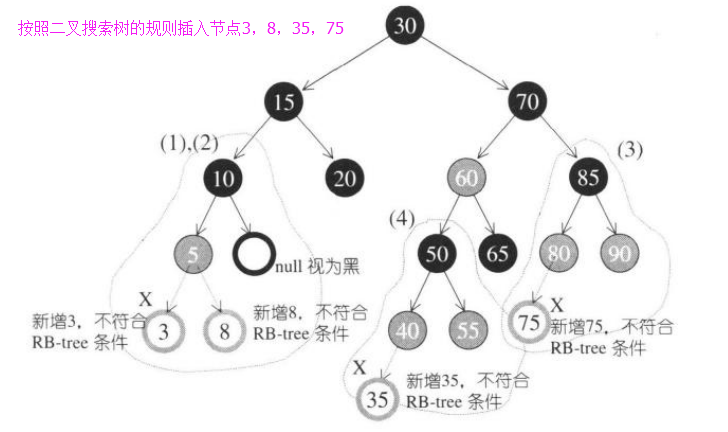
插入節點：

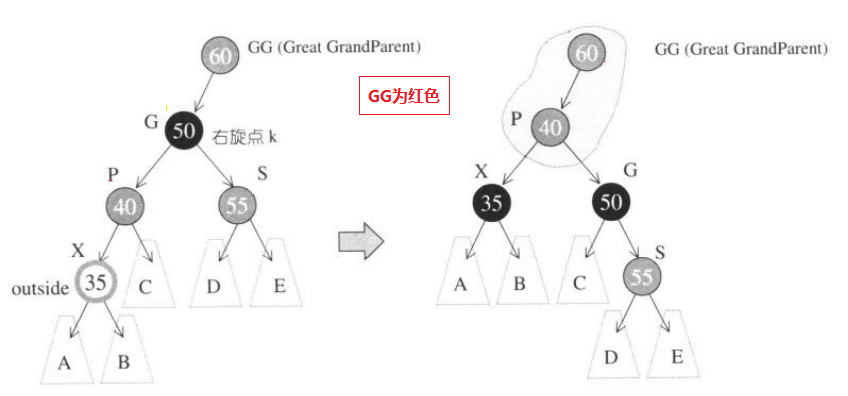
如果新增節點根據二叉搜尋樹的規則到達插入點時，不能符合上面兩個規則，則必須調整顏色並旋轉樹形。如下圖所示則需要調整：





設新節點為X，其父節點為P，祖父節點為G，伯父節點（父節點的兄弟節點）為S，曾祖父節點為GG。
根據二叉搜尋樹的規則新節點必須為葉節點。再根據規則4，新節點必須為紅色。所以如果P也為紅則需要調整（G此時肯定為黑）。如果P為黑色，則不用調整。

只有在新增節點（必須為紅色）的父節點也為紅色的時候才需要調整。（也就是說RB樹中不能出現父子節點同時為紅色）

具體情況有下面四種：

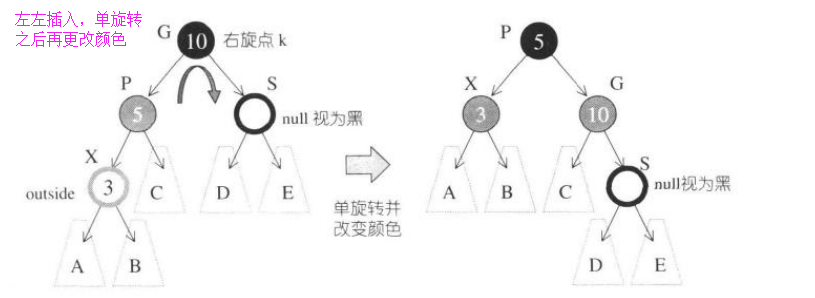
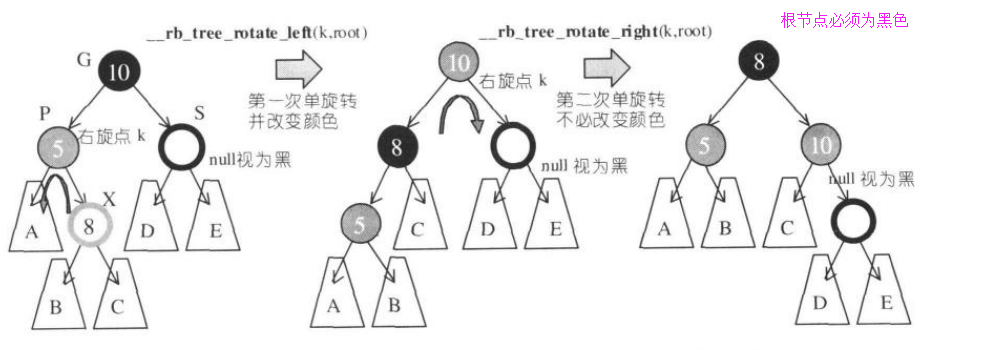
1.S為黑且X為外側插入：先對P,G做一次單旋轉，再更換P,G的顏色。





2.S為黑且X為內側插入：先對P,X做一次單旋轉，再更換G，X的顏色。最後再對G做一次單旋轉。




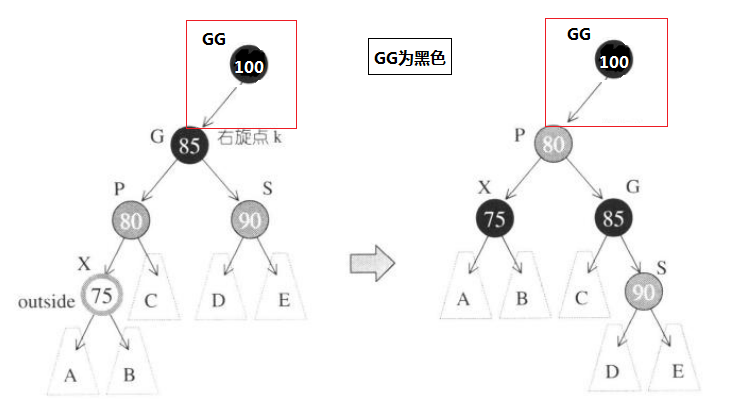
3.S為紅且X為外側插入：先對P,G做一次單旋轉，再更改X的顏色。如果此時GG為黑，則一切搞定。




4.S為紅且X為外側插入：先對P,G做一次單旋轉，再更改X的顏色。如果此時GG為紅色，還要繼續向上按剛才的步驟旋轉並更改顏色。




參考文章：紅黑樹、插入刪除操作

相關文章