資料結構與演算法——AVL樹簡介

readyao發表於2016-03-27
資料結構演算法

電腦科學中的樹

二叉樹
▪ 二叉樹 ▪ 二叉查詢樹 ▪ 笛卡爾樹 ▪ Top tree
▪ T樹      
 
自平衡二叉查詢樹
▪ AA樹 ▪ AVL樹 ▪ 紅黑樹 ▪ 伸展樹
▪ 樹堆 ▪ 節點大小平衡樹    
 
B樹
▪ B樹 ▪ B+樹 ▪ B*樹 ▪ Bx樹
▪ UB樹 ▪ 2-3樹 ▪ 2-3-4樹 ▪ (a,b)-樹
▪ Dancing tree ▪ H樹    
 
Trie
▪ 字首樹 ▪ 字尾樹 ▪ 基數樹  
 
空間劃分樹
▪ 四叉樹 ▪ 八叉樹 ▪ k-d樹 ▪ vp-樹
▪ R樹 ▪ R*樹 ▪ R+樹 ▪ X樹
▪ M樹 ▪ 線段樹 ▪ 希爾伯特R樹 ▪ 優先R樹
 
非二叉樹
▪ Exponential tree ▪ Fusion tree ▪ 區間樹 ▪ PQ tree
▪ Range tree ▪ SPQR tree ▪ Van Emde Boas tree  
 
其他型別

▪ 堆 ▪ 雜湊樹 ▪ Finger tree ▪ Metric tree
▪ Cover tree ▪ BK-tree ▪ Doubly-chained tree ▪ iDistance
▪ Link-cut tree ▪ 樹狀陣列  


二叉樹：

任何節點最多隻允許有兩個子節點。

二叉搜尋樹：

可以提供對數時間的元素插入和訪問。任何節點的鍵值一定大於其左子樹中的每一個節點的鍵值，並不小於其右子樹中的每一個節點的鍵值。

平衡二叉搜尋樹：

平衡的意思是，沒有任何一個節點過深（深度過大）。二叉搜尋樹可能會在多次插入或刪除之後，變得不平衡。


AVL-tree、RB-tree和AA-tree均可實現出平衡二叉搜尋樹。

AVL-tree是一個"加上了額外平衡條件"的二叉搜尋樹，其平衡條件的建立是為了確保整棵樹的深度為O(logN)。要求任何節點的左右子樹高度相差最多1。

根節點到任一節點的路徑長度，即所謂該節點的深度。根節點的深度永遠為0.


平衡樹和不平衡樹的區別：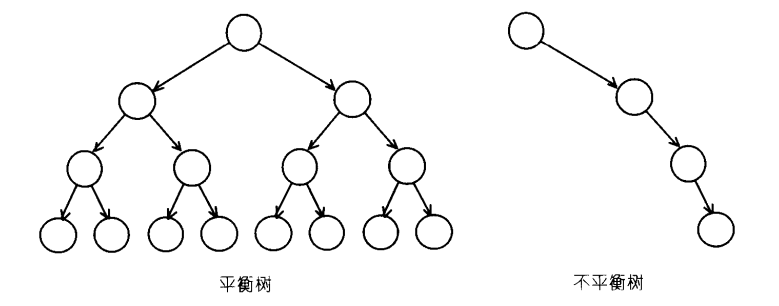



插入節點11之後，樹變得不平衡了：



插入節點破壞了平衡條件的四種情況：



情況1，4對稱，稱為外側插入，可以採用單旋轉操作調整解決。

情況2，3對稱，稱為內側插入，可以採用雙旋轉操作調整解決。






單旋轉（旋轉的情況為外側插入）：




雙旋轉（旋轉的情況為內側插入）：



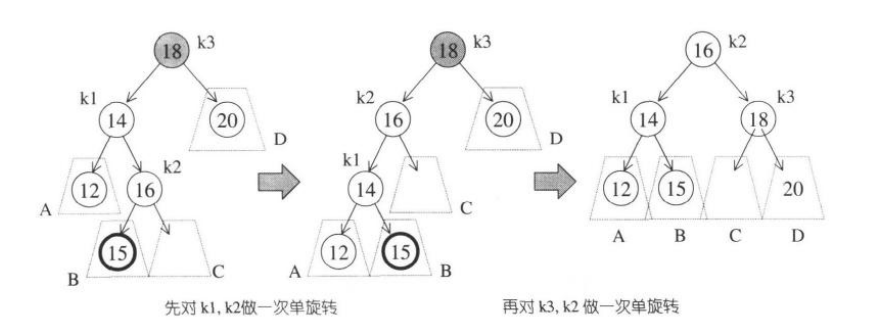
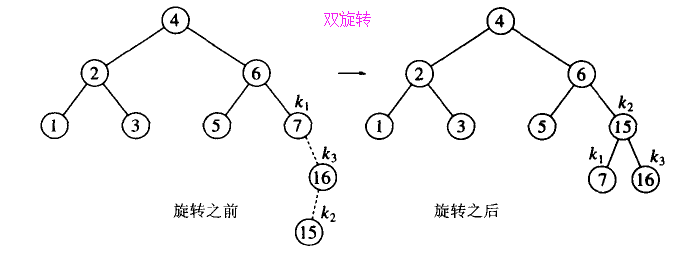
對於雙旋轉的情況，有一個特殊之處，比如上圖，因為插入了15，引起了18的不平衡。15肯定是介於18和18的左子樹之間的值。此時肯定要雙旋轉。
如果15的父節點不是18的子節點（上面的情況）雙旋轉其實就是將15的父節點代替18結點。(當然還是要旋轉的，這只是一個特點)
如果15的父節點16是7的子節點（下面的情況）雙旋轉其實就是將15節點代替7結點。(當然還是要旋轉的，這只是一個特點)






相關文章