《圖論》——最短路徑 Dijkstra演算法(戴克斯特拉演算法)

十大演算法之Dijkstra演算法：

最短路徑是圖論演算法中的經典問題。圖分為有向圖、無向圖，路徑權值有正值、負值，針對不同的情況需要分別選用不同的演算法。在維基上面給出了各種不同的場景應用不同的演算法的基本原則：最短路問題。

針對無向圖，正權值路徑，採取Dijkstra演算法。

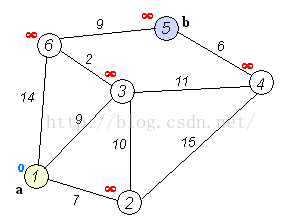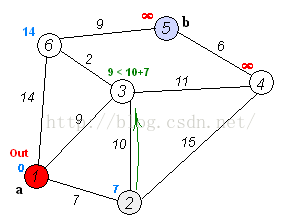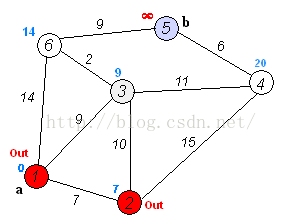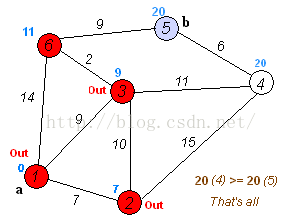
如上圖，是求a到b的最短路徑，這裡並不限定b節點，修改為到任意節點的路徑，問題是完全一樣的。

首先需要記錄每個點到原點的距離，這個距離會在每一輪遍歷的過程中重新整理。每一個節點到原點的最短路徑是其上一個節點（前驅節點）到原點的最短路徑加上前驅節點到該節點的距離。以這個原則，經過N輪計算就能得到每一個節點的最短距離。

第一輪，可以計算出，2、3、4、5、6到原點1的距離分別為：[7, 9, -1, -1, 14]。-1表示無窮大。取其中最小的，為7，即可以確定1的最短路徑為0，2為下一輪的前驅節點。同時確定2節點的最短路徑為7，路線：1->2。

第二輪，取2節點為前驅節點，按照前驅節點的最短距離加上該節點與前驅節點的距離計算新的最短距離，可以得到3，4，5，6節點到原點的距離為：[17, 22, -1, -1]，此時需要將這一輪得到的結果與上一輪的比較，3節點：17 > 9，最短路徑仍然為9；4節點：22 < 無窮大，重新整理4節點的最短路徑為22；5節點：不變，仍然為無窮大；6節點：14 < 無窮大，取14，不變。則可以得到本輪的最短距離為：[9, 22, -1, 14]，取最短路徑最小的節點，為3，作為下一輪的前驅節點。同時確定3節點的最短路徑為9，路線：1->3。

第三輪，同上，以3為前驅節點，得到4，5，6的計算距離為：[20, -1, 11]，按照取最短路徑的原則，與上一輪的進行比較，重新整理為：[20, –1, 11]，選定6為下一輪的前驅節點。同時取定6的最短路徑為11，路線：1->3->6。

第四輪，同上，以6為前驅節點，得到4和5的計算距離為[20, 20]，與上一輪進行比較，重新整理後為[20, 20]，二者相等只剩下兩個節點，並且二者想等，剩下的計算已經不需要了。則兩個節點的最短路徑都為20。整個計算結束。4的最短路徑為20，路線：1->3->4。5的最短路徑為20，路線：1->3->6->5。

如果二者不相等，則還需要進行第五輪，先確定二者中的一個的最短路徑和路線，再取定剩下的。直到整個5次迴圈都完成。

程式碼如下：

package Graph;

/*
 *Dijkstra，最短路徑演算法 
 */

public class Dijkstra {

	public static final int M = -1;
	static int[][] map = {
		{ 0,  7,  9,  M,  M, 14 }, 
        { 7,  0,  10, 15, M, M },
        { 9,  10, 0,  11, M, 2 }, 
        { M,  15, 11, 0,  6, M },
        { M,  M,  M,  6,  0, 9 }, 
        { 14, M,  2,  M,  9, 0 }
	};
	static int n =map.length;       //頂點的個數
	static int[] shortest = new int[n];  //存放從start到其他節點的最短路徑
	static boolean[] visited = new boolean[n]; //標記當前該頂點的最短路徑是否已經求出，true表示已經求出
	
	public static void main(String[] args) {
		int orig = 0; //起始點
		//尋找最短路徑
		int[] shortPath = dijkstra_alg(orig);
		
		if(shortPath == null){
			return;
		}
		
		for(int i=0; i< shortPath.length; i++){
			System.out.println("從" + (orig + 1) + "出發到" + (i + 1) + "的最短距離為："+ shortPath[i]);
			}
	}

	private static int[] dijkstra_alg(int orig) {
		// TODO Auto-generated method stub
		// 初始化，第一個頂點求出
        shortest[orig] = 0;
        visited[orig] = true;
		for(int count = 0; count != n-1; count ++)
		{
			//選出一個距離初始頂點最近的為標記頂點
			int k = M;
			int min = M;
			for(int i =0; i< n ; i++)//遍歷每一個頂點
			{
				if( !visited[i] && map[orig][i] != M) //如果該頂點未被遍歷過且與orig相連
				{
					if(min == -1 || min > map[orig][i]) //找到與orig最近的點
					{
						min = map[orig][i];
						k = i;
					}
				}
			}
			//正確的圖生成的矩陣不可能出現K== M的情況
			if(k == M)
			{
				System.out.println("the input map matrix is wrong!");
				return null;
			}
			shortest[k] = min;
		    visited[k] = true;
			//以k為中心點，更新oirg到未訪問點的距離
		    for (int i = 0; i < n; i++)
            {
                if (!visited[i] && map[k][i] != M)
                {
                    int callen = min + map[k][i];
                    if (map[orig][i] == M || map[orig][i] > callen)
                    {
                    	map[orig][i] = callen;
                    }
                }
            }
		}
		
		return shortest;
	}
}

執行結果如下：

從1出發到1的最短距離為：0
從1出發到2的最短距離為：7
從1出發到3的最短距離為：9
從1出發到4的最短距離為：20
從1出發到5的最短距離為：20
從1出發到6的最短距離為：11