RSA演算法以及數學基礎

RSA演算法及數學基礎

1. 公鑰體制數學基礎

由於傳統金鑰體制出現了困難，例如2000個使用者保密通訊每個人需要儲存1999個金鑰（兩兩保密通訊需要共（2000*19999）/2 = 1999000個金鑰，每人保管1999個），在金鑰管理分配上有困難。另外由於數字簽名（身份認證）的需要增加。

公鑰體制解決了上述兩個問題，即每個人有一對金鑰（公鑰和私鑰），將公鑰公開，私鑰自己保管，這樣每人只要保管好自己的私鑰就可以了。通訊時使用收信方的公鑰進行加密，收信方使用私鑰進行解密。在身份認證時，簽名者使用私鑰簽名，驗證簽名者使用簽名者的公鑰驗籤。當然在實際應用時還有其他的問題需要保證，例如抗抵賴，保持資訊的完整性等密碼學問題。在本文中先不考慮。

有上述公鑰體制的任務中我們知道，區別於其他金鑰體制演算法，公鑰演算法需要做到的是將加密金鑰（公鑰）和加密演算法公開，破壞者也不能由公鑰和密文破譯出明文。只有使用解密金鑰（私鑰）和解密演算法才能解出明文。而且保證通過公鑰不能推出私鑰。

上述內容可以通過所謂的“單向函式”來實現。（傳統的金鑰體制中加密演算法和解密演算法是互逆的。）所謂“單向函式”是指加密函式E和解密函式D。但是已知加密函式E推導其逆運算卻非常困難（也就是推導私鑰的過程）。所以若不知道解密函式（或私鑰）不可能解出明文。

單向函式的實現依賴的是大整數因子分解的難度，根據

算數基本定理：任何大於1的整數都可以分解成素數乘積的形式，並且，如果不計分解式中素數的次序，該分解式是唯一的[微軟中國1]。

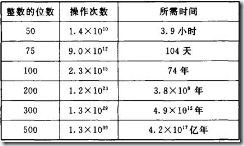
這個定理在理論上十分漂亮，但是操作起來卻非常困難下表列出了現代最快的分解演算法在大型計算機上分解一個大數所用的時間。

2. RSA相關的數論知識

1. 一個大於1的整數p，若除1和起本身之外沒有其他正整數因數（約數），稱P為素數。

2. 若整數a和b最大公約數為1，則稱a，b互素，記為（gcd（a，b）= 1）。

3. 設n為正整數，a和b為整數，若a和b被n除後所得餘數相同，稱a和b模n同餘，記為a≡b（mod n）。此式被稱為同餘式。若n能整除a則同餘式表示為a≡0（mod n）。

兩個整數模n同餘的等價說法有：a和b被n除餘數相同。a-b被n整除。a和b在模n的同一個剩餘類中。存在整數s使得a=sn+b。

4. 同餘式的一些運算性質，

（1） 若a≡b（mod n），c≡d（mod n）則有ac≡bd（mod n）。特別的有，ka≡kb（mod n），k為任意整數。

（2） 若a≡b（mod n），d是a，b，n的公因數，則(a/d) ≡(b/d)（mod n/d）。特別的有aⁿ≡bⁿ（mod n），n為正整數。[微軟中國2]

（3） 若ka≡kb（mod n），且k與n互素時，有a≡b（mod n）。（同餘式消去律）

5. 設n為正整數 ,則任何一個整數被n除 ,餘數必為0,1,2,…,n-1中的某一個,把整數集中被n除餘數相同的數分別歸為一類,記為[0],[1],[2]…,[n-1],這樣就按模是否同餘把整數集分成n類,其中每一類都稱為模n的一個剩餘類。顯然,每個整數必屬於上述類中的一類,被n除餘數不同的數必屬於上述的不同類中。若a0,a1,a3…,an-1分別取自上述類的不同類中,稱a0,a1,a3…,an-1為模n的一個完全剩餘系,該剩餘系中的數兩兩模n不同餘。

6. 含有未知量的同餘式稱為同餘方程。一次同餘方程是最簡單的一種,其一般形式為ax≡b（mod n）。若a，n的最大公約數d能整除b，則ax≡b（mod n）有解。且恰有d個解。若a，n的最大公約數d不能能整除b，則ax≡b（mod n）無解。例如同餘方程7x≡1（mod 5）。7與5最大公約數為1，能被b=1整除，故有一個解。7x≡1（mod 5）≡6≡11≡21（mod5）。由於7與5互素有消去律得x=3。.[微軟中國3]
一般地 解同餘方程的步驟為 ①判斷解的情況 ②當同餘方程的a，b，n有公因數時 ,約去公因數化簡方程 ③利用同餘的定義和消去律求方程的解。

7. 費馬小定理：設任意整數a和素數p互素[微軟中國4] ，則a^p-1 ≡1（mod p）。

8. 尤拉定理：若n,a為正整數，且n,a互質，(a,n) = 1，則a^φ(n) ≡ 1 (mod n)。

9. 模運算極其性質：

基本理論:

基本概念：

給定一個正整數p，任意一個整數n，一定存在等式 n = kp + r ；

其中k、r是整數，且 0 ≤ r < p，稱呼k為n除以p的商，r為n除以p的餘數。

對於正整數p和整數a,b，定義如下運算：

取模運算：a % p（或a mod p），表示a除以p的餘數。

模p加法：(a + b) % p ，其結果是a+b算術和除以p的餘數，也就是說，(a+b) = kp +r，則(a + b) % p = r。

模p減法：(a-b) % p ，其結果是a-b算術差除以p的餘數。

模p乘法：(a * b) % p，其結果是 a * b算術乘法除以p的餘數。

說明：

1. 同餘式：正整數a，b對p取模，它們的餘數相同，記做 a ≡ b % p或者a ≡ b (mod p)。

2. n % p得到結果的正負由被除數n決定,與p無關。例如：7%4 = 3， -7%4 = -3， 7%-4 = 3， -7%-4 = -3。

基本性質:

（1）若p|(a-b)，則a≡b (% p)。例如 11 ≡ 4 (% 7)， 18 ≡ 4(% 7)

（2）(a % p)=(b % p)意味a≡b (% p)

（3）對稱性：a≡b (% p)等價於b≡a (% p)

（4）傳遞性：若a≡b (% p)且b≡c (% p) ，則a≡c (% p)

運算規則

模運算與基本四則運算有些相似，但是除法例外。其規則如下：

     (a + b) % p = (a % p + b % p) % p （1）

     (a - b) % p = (a % p - b % p) % p （2）

     (a * b) % p = (a % p * b % p) % p （3）

     (a^b) % p = ((a % p)^b) % p （4）

結合率： ((a+b) % p + c) % p = (a + (b+c) % p) % p （5）

     ((a*b) % p * c)% p = (a * (b*c) % p) % p （6）

交換率： (a + b) % p = (b+a) % p （7）

     (a * b) % p = (b * a) % p （8）

分配率： ((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p （9）

重要定理

      若a≡b (% p)，則對於任意的c，都有(a + c) ≡ (b + c) (%p)；（10）

若a≡b (% p)，則對於任意的c，都有(a * c) ≡ (b * c) (%p)；（11）

若a≡b (% p)，c≡d (% p)，則 (a + c) ≡ (b + d) (%p)，(a - c) ≡ (b - d) (%p)，

(a * c) ≡ (b * d) (%p)，(a / c) ≡ (b / d) (%p)； （12）

若a≡b (% p)，則對於任意的c，都有ac≡ bc (%p)； （13）

3. RSA演算法及證明：

1. RSA定理證明：

定理：設p，q是不同的素數，n=pq記φ(n)=(p-1)(q-1),如果e，d是與φ(n)互素[微軟中國5] 的兩個正整數（e,d<φ(n)),並滿足ed≡1(mod φ(n)),則對於每個整數x,都有x^ed≡x(mod n)。

分析：為了證明x^ed≡x(mod n)，只要證明φ(n)是x^ed-x的因數即可。又因為n=pq，而p，q都是素數，故只要證明p和q都是x^ed-x的因數即可[微軟中國6] ，即

x^ed≡x(mod p) （1）

x^ed≡x(mod q) （2）

證明：證明式1，若p是x的因數則式1必然成立
若p不是x的因數，則由ed≡1(mod φ(n))得ed-1=k(p-1)(q-1),k為任意整數。則x^ed=x^{k(p-1)(q-1)+1} = x*（x^p-1）^k(q-1)
根據費馬小定理因為x與p互素所以x^p-1≡1（mod p）
所以x^ed≡x*（1）^k(q-1) ≡x（mod p）[微軟中國7]
同理可證x^ed≡x(mod q)

2. RSA定理與RSA加密演算法：
RSA加密演算法為：
(1) 取兩個大素數p,q (保密)；
(2) 計算 n=p*q (公開), φ(n)=(p-1)*(q-1) (保密)；
(3) 隨機選取整數e，滿足 gcd(e, φ(n))=1 （e與φ(n)互素）(公開)；
(4) 計算 d 滿足 d*e≡1 (mod φ(n)) (保密)； （d為e的逆元，可通過擴充套件的歐幾里得演算法進行求解）
(5) ｛e，n｝為公鑰，｛d，n｝為私鑰，也可以用｛e，d｝表示金鑰對
(6) 加密時c = x^e mod n ；解密時 x = c^d mod n
(7) 簽名時c = x^d mod n ；解密時 x = c^e mod n
問題：為什麼x^ed≡x(mod n) 就能保證(6)和(7)正確？
分析：解x^ed≡x(mod n)同餘式方程，該方程可能有n個解[微軟中國8] ，這n個解都在模n的同一個剩餘類中，小於n的解只有一個，由於明文小於n[微軟中國9] ，則該解即是明文x。而x^ed mod n得到的就是小於n的那個解。
另外，注意密文c並不等於x^e而是c≡x^e（mod n）。這裡有上一段中我們知道要想求出明文x，解同餘式方程x^ed≡x(mod n)可得，這時只要等式左邊的數與X同餘就能得到正確的明文。由於c≡x^e（mod n），所以可得c^d≡x^ed（mod n）,所以c^d≡x^e（mod n）。

3. 從另一個角度解釋為什麼RSA加密和解密過程是互逆的：
將問題改為證明：A^e mod n = B^(e*d)mod n-----------1
即B^(e*d)mod n = B
其中A為密文，B為明文。
證明：因為ed+1=（p-1）（q-1）所以B^(e*d)=B^(k(p-1)(q-1)+1),
當B與n互素時，根據尤拉定理有:
B^(k(p-1)(q-1)+1) mod n
= B*B^ k(p-1)(q-1) mod n
= (B mod n )*((B^(p-1)(q-1))^k mod n)
= (B mod n ) * (((B^(p-1)(q-1)) mod n) ^ k ) mod n)
= B * (1^k mod n)
=B[微軟中國10]
當B與n不互素時，由於n=p*q，B必然能被p或者q整除，假設B=k*p[微軟中國11] ,則B與q互素。再運用費馬定理有：
B^(q-1) = 1 mod q，
則（B^(q-1)）^(p-1)K = 1^(p-1)K mod q = 1 mod q,
即B^k(p-1)(q-1) mod q =1。
兩邊同時乘以B，得到
B^(k(p-1)(q-1)+1) mod q = B
也就是B^(e*d)mod n = B

4. RSA演算法舉例：
公鑰體制中,單向函式的構造基於大整數n因數分解的困難 ,因而n的兩個因數p與q都應取大素數。為便於理解,我們選取兩個較小的素數來說明該體制的實施。
例：給定兩個素數p=13，q=17
（1）為使用者A和B設計公鑰和私鑰。
（2）使用者A將明文x=3 加密。
（3）使用者A將明文x=3 加密並簽名後發給B，B解密並驗證簽名試把加密通訊過程詳細寫出。
解：（1）計算得n=p*q=221，φ(n)=（p-1）*（q-1）=12*16=192。

隨機選取與φ(n)=192互素的兩個數e1=7和e2=13，並建立同餘方程

7x≡1（mod 192）

13x≡1（mod 192）

由於7和192；13和192都互素，7x ≡1 ≡ 193 ≡ 385 mod 192，根據消去律得到x = 55即d1=55，同理得到d2 =133.

將金鑰｛7，55｝和｛13.133｝交給A和B兩個人。將n，e1，e2公開，d1，d2交給A和B各自祕密保管。φ(n)=192由金鑰製作者保管。

（2）A在公鑰簿上查詢到B的公鑰e2=13，得到加密函式
E₂(x) ≡ x^13 (mod 221),對資訊x=3進行加密得到密文y≡ 3^13 (mod 221)

因為3^2≡9(mod 221);3^4≡9*9≡81(mod 221);3^8≡81*81≡6561≡152(mod 221)[微軟中國12]

所以，3^13 ≡ 3^(8+4+1) ≡152*81*3 ≡ 29 (mod 221)

A將密文29發出給B。

B使用自己的私鑰133進行解密x = D₂（y）≡ y^133 ≡ 29^133(mod 221). 用上述方法計算得29^4 ≡ 81 (mod 221); 29^128 ≡ 35 (mod 221);所以，29^133 ≡ 29^(128+4+1) ≡ 35*81*29 ≡ 3 (mod 221)。

B得到明文3。

（3）A使用自己的私鑰55和解密函式對資訊x=3進行簽名得y=3^55 mod 221.A在從公鑰簿上查詢B的公鑰為13和B的加密函式，對y進行加密z=y^13 mod 221 = 3^（55*13）mod 221 = 3^153 mod 221.

計算得z=211。

B得到密文後，先查到A的公鑰7，用7解密密文z=211，得到y。在使用自己的私鑰對y進行驗證得到資訊x=3。[微軟中國13]

---

[微軟中國1]分解式中因數的個數是固定的嗎？

是，因為素數不能再分了。即使已知一個大數能分成倆個素數的乘積（已知因數個數）其分解仍然很難嗎？

[微軟中國2]自己想的

[微軟中國3]同餘方程中若a與n互素則方程必有且只有一個解，這也是RSA加解密函式中使用的。

[微軟中國4]即使兩個和數也可以互素例如8和27

[微軟中國5]為什麼e要與φ(n)互素？因為只有e和φ(n)互素了，同餘方程ed≡1(mod φ(n))才有且僅有一個解。

[微軟中國6]兩個數的最小公倍數=p*q/兩個數的最大公約數，若兩個數互素（不一定非得全是素數）則兩數最大公約數為1，即互素的兩個數的最小公倍數就是這兩個數的積。而兩個數的公倍數都是其最小公倍數的倍數。所以n=pq是p和q的最小公倍數，而只要證明x^ed-x是p和q的公倍數（即q和p都是x^ed-x的因數）就可以證明n是x^ed-x的因數。

前提是x^ed-x > n???

[微軟中國7]根據上述同餘式的運算性質（2）：

因為x^p-1≡1（mod p），

所以（x^p-1）^k(q-1) ≡1（mod p）

根據同餘式的運算性質（1）：

所以x*（x^p-1）^k(q-1)≡x（mod p）

[微軟中國8]為什麼必有解？因為a是b的倍數？因為未知數本身就是模n的剩餘類，而模n的剩餘類肯定是存在的。

[微軟中國9]注意明文必須小於n。

[微軟中國10]參考模運算規則。

[微軟中國11]Why？

[微軟中國12]與直接求3^13不同

[微軟中國13]先簽名在加密。