前文：
數字媒體技術揭祕

四、壓縮技術

4.1 理論基礎

廿世紀中葉，為了從理論上證明對資訊系統進行優化的可行性，Shannon引入了熵的概念，用來表示資訊的不確定性，熵越大，資訊的不確定性就越大[4]，而資訊的不確定性越大，其對應的傳輸和儲存成本就越高。換句話說，如果某種資訊的熵不是那麼大，則人們應該有信心使用有限的資源去承載它。舉一個簡單的例子，假設氣象臺負責預報明天是否天晴，而地震局負責預報明天是否地震，那麼顯然，來自氣象臺的資訊要比來自地震局的資訊具有更大的不確定性，也就是說氣象資訊的熵更大，如若使用喇叭來傳遞資訊，對於氣象臺而言，以鳴喇叭來表示天晴或者表示天陰，對喇叭的使用壽命影響並不大，地震局則不然，如果以鳴喇叭來表示地震，那這喇叭的使用壽命遠大於氣象臺的那一隻。這說明，資訊傳輸的成本是有下限的，這個下限由信源的熵決定，而如何達到或接近這個下限成為通訊領域的主要研究內容，資料壓縮便是其中的主題之一，在Shannon的通訊模型中屬於信源編碼的範疇。

通過建立一個簡化的信源模型可以算出熵的最大值，這是非常有意義的，基於這個最大熵可以得到傳遞資訊的極限成本。離散平穩無記憶信源就是這樣的一個簡化模型，源自這種信源的資訊統計特性相同，但相互獨立，於是可以用一個概率空間[M, P]來抽象這些資訊，其中M={M1, M2, …, Mk}是概率分佈為P={P1, P2, …, Pk}的一個隨機變數，那麼M的熵由下面公式給出：

公式中−log₂Pi表示Mi的資訊量：概率越大資訊量越小。於是不難發現，H(M)不過是資訊量的一個概率平均。對於離散平穩無記憶信源，H(M)也可以看作信源的熵，針對某種特定的分佈，這個熵存在最大值，對應的分佈叫做最大熵分佈。離散無記憶信源的最大熵分佈是均勻分佈，此時其熵值為log₂(k)，k是其可能值的個數。

如果信源是有記憶的，也就是說信源產生的資訊相互並不獨立，則需要引入聯合熵的概念。以兩個相關的隨機變數表示信源產生的兩個資訊來構造一個最簡單的模型，以下三個公式成立：

H(X,Y) = H(X)+H(Y)-I(X,Y) (4-1)
I(X,Y) = H(X)-H(X|Y) = H(Y)-H(Y|X) (4-2)
H(X|Y) = H(X,Y)-H(Y) (4-3)

其中，H(X,Y)為聯合熵，表示這兩個資訊整體上的不確定性；I(X,Y)為互資訊量，表示兩個資訊的相關性，不相關的資訊互資訊量為0；H(X|Y)叫做相對熵，表示在Y已知的情況下X的不確定性。第一個公式說明，對於相關的資訊，其各自熵的和會大於描述其整體不確定性的聯合熵。第二個公式定義兩個資訊的互資訊量為其中一個的熵減去其相對熵。第三個公式表示，X在Y已知的情況下的相對熵等於兩個資訊的聯合熵減去Y的熵。

對於有記憶信源，其熵值不再等於其產生的某一個的資訊的熵，這種情況下要使用熵率來描述信源的不確定性，這是一個極限值，假設Hn是信源產生的n個資訊的聯合熵，則熵率就是n趨於無窮大時的Hn/n。

資料壓縮就是對信源產生的資訊進行編碼的一個過程，即使用某個符號表，如0和1來表示要傳輸的資訊。這裡涉及到兩種情形：無損編碼和有損編碼。對於無損編碼來說，要求解碼之後的資訊和編碼之前的資訊完全相同，即編碼過程不引入任何失真，在這種情況下，如果使用二進位制符號來表示信源產生的某個資訊，其平均長度不能小於資訊的熵或信源的熵率。有損編碼則會在編碼過程中引入失真，因此，從根本上講是一個資訊率-失真最優化的問題。

假設編碼過程引入的均方失真為D，則存在一個函式R(D)，表示不超過給定失真D的前提下對該信源編碼所需要的最小的資訊率，即所謂的率失真函式。如果信源的概率分佈給定，平均失真D僅由信源編碼前後的轉移概率——亦即編碼方式決定，則率失真函式給出的其實是一個信源編碼的極限資訊率，也就是說，對於既定信源，總可以找到一種編碼方式，能夠保證在既定失真的前提下達到率失真函式給出的最小資訊率。率失真函式取決於信源的統計特性，一般不存在顯式的表示式，但是對於某些特定分佈的信源，率失真函式能夠以明瞭的形式給出，比如高斯分佈的連續無記憶信源的率失真函式為：

再舉一個二值的離散無記憶信源X的例子：概率P分別為0.1、0.2、0.3和0.5的情況下其率失真函式如下圖示：

可以發現，當P=0.5，即均勻分佈的情況下，資訊率失真函式最靠上，也就是說給定最小失真對應的極限資訊率越大。當失真為零時，資訊率的極限為1，亦即信源的熵。也就是說，有這樣一個信源，它以50%的概率在產生符號0和符號1，則無失真地編碼該信源產生的一個符號最少也需要1個位元，注意，這是傳輸成本最高的一種信源。此時，我們便不難理解氣象臺的喇叭為什麼更容易損壞了。

4.1.1 變換編碼

從理論上講，變換的主要目的是去相關。由公式4-1可知，對於相關性很強的兩個隨機變數，其互資訊非常大，導致兩個信源的熵的和遠大於其聯合熵。如果將這兩個隨機變數看做為一個二維的隨機向量，通過一個變換矩陣，可以將{X, Y}變換為 {X’, Y’}，在這一過程中，H(X,Y)=H(X’,Y’)，如果變換矩陣選擇適當，令I(X’,Y’)=0，則H(X’)和H(Y’)將遠小於H(X)和H(Y)，從而對X’和Y’編碼需要的位元數將大大減少。能夠使X’和Y’相互獨立的變換叫做KL變換，這是一種理論上的最佳變換，但由於相應的變換矩陣需要通過X和Y的統計特性來計算，在工程上很難應用起來。

可以從更直觀的角度來理解這種說法：以影像資料為例，假設每個畫素點的亮度範圍為0~255，則在空間域獨立地來看某個畫素點的話，其統計特性是近似均勻的，也就是說，各階畫素值發生的概率大致都差不多，因此，至少需要8個位元編碼一個畫素值，而不能夠給某些畫素值多些的位元，而給某些值少一些。但實際上，對於一個來自某幅影像的畫素矩陣取樣，如果其中某個畫素點為值0的話，其它點為255的概率也不會太大。如下圖所示，左圖是典型的影像資料（取樣自Lenna），而右圖則極為罕見，在編碼的時候，左圖資料應該給以多於右圖資料的位元數，要達到這樣的目標，在缺少完美的向量量化方法之前，變換不失為一種很好的工具。

那麼，變換域中各點取值的概率分佈又如何呢？首先，各點的值域將發生變化，比如DCT變換域各點的取值範圍為-2048~2048；其次，各點的概率分佈更加獨立。 還以上面兩幅影像為例，與罕見的影像取樣（右圖）相比，經典的影像取樣（左圖）變換域右下方向的值更接近0。因此，對於影像資料來說，變換域右下角出現大量0值是比較常見的，可以使用更少的位元編碼這些大概率的情況。換句話說，變換是為了從全域性的角度抽取一組資料的特徵，並將這些特徵分割開來。

DCT是音視訊壓縮中的一種常用變換，它雖然不能保證使變換後的隨機變數相互獨立，但仍能大大減少它們的相關性，而且，DCT變換還能產生能量聚集的效果，即對於變換後的隨機向量，能量相對集中在索引較小的分量上，更有利於量化。

4.1.2 差分編碼

差分編碼基於預測來實現，即不編碼原始信源資料，而去編碼原始信源資料和預測資料的差分資料，主要目的是在不引入失真的前提下減小原訊號序列的動態範圍。假設信源產生了一個隨機序列：

S(0), ..., S(n-5), S(n-4), S(n-3), S(n-2), S(n-1), S(n)

設S’(n)為S(n)的預測值：

S'(n) = f(S(n-1), S(n-2), S(n-3), S(n-4), S(n-5))

則預測值序列為：

S'(0), ..., S'(n-5), S'(n-4), S'(n-3), S'(n-2), S''(n-1), S(n)

令d(n) = S(n)-S’(n)，則差分序列為：

d(0), ..., d(n-5), d(n-4), d(n-3), d(n-2), d(n-1), d(n)

預測的準則是均方誤差最小，及找到一個合適的預測函式f，使d²(n)最小。 與變換編碼不同之處是，即使找到了一個最優的預測函式f，差分編碼也不一定會提高編碼效率。如果隨機序列中個分量不具備相關性甚至是負相關的，差分序列中個分量的均方差會變得很大，甚至大於原始序列中各分量的均方差，這種情況下編碼效率會嚴重下降。

對於一個相關係數接近1的馬爾可夫序列，S’(n)=S(n-1)是一個較優的預測函式，這種差分編碼便是廣泛使用的DPCM技術。

需要注意的是，在實際的編碼過程中，由於解碼端無法得到原始值，所以預測函式通常使用預測值來代替原始值，即：

S'(n) = f(S'(n-1), S'(n-2), S'(n-3), S'(n-4), S'(n-5))

對於DPCM，S’(n)=S’(n-1)

4.1.3 熵編碼

通過變換和預測等方法使信源的統計特性得到一定的改善之後（去相關性，降低均方差……），接下來需要進行的是熵編碼，也是資料壓縮的最後一步，其主要責任是將壓縮視訊的各種頭資訊、控制資訊以及變換系數轉換為二進位制的位元流。有兩種最基本的熵編碼方法：

• 定長編碼: 對所有的待編碼資訊使用相同長度的碼字
• 變長編碼: 使用不同長度的碼字

假設某個待編碼的資訊元素A∈{A0, A1, …, An}，如果採用定長編碼，需要的位元數為log₂(n)取整，而使用變長編碼，其平均碼長的極限取決於該資訊的熵H，除非是均勻分佈，不然所需要的位元數必定小於log₂(n)。因此，如果某個資訊元素在概率分佈上是極度不均勻的，通常都會採用變長編碼的方式，即概率小的值使用長碼字，概率大的值使用短碼字。

指數哥倫布碼、Huffman編碼和算術編碼都是常用的變長編碼方法。

4.1.4 量化

量化[5]是一種多對一的對映，是引入失真的一個過程，也是限失真信源編碼技術的基礎。無論是對時間取樣後的模擬訊號進行數字化的過程，還是對數字序列進行有失真壓縮的過程，都需要完成一個由輸入集合到輸出集合的對映，這個對映是由量化來實現的。

最簡單的量化方法是將單個樣本的取值進行量化，因為被量化的變數是一維的，所以這種量化方法叫做標量量化。設n階標量量化器的輸入為連續隨機變數x，輸出為離散隨機變數y，其中：

x∈(A0, An)， y∈{Y1, Y2, …, Yn}，A0≤ Y1 ≤ A1 ≤ Y2 ≤ …… An-1 ≤ Yn ≤ An。
則y 的取值由下式決定：

當量化階數n一定時，選擇合適的Ai 和Yi 可以使量化器的平均失真最小，這時的量化稱為最佳標量量化。若輸入變數x滿足均勻分佈，可以將(A0, An)均勻分割成n個小區間，每個小區間的中點作為量化值。這種量化方法叫做均勻量化，對於均勻分佈的輸入變數來說，均勻量化是最佳標量量化。當採用均方失真函式時，可以計算出其平均失真為Δ²/12，其中Δ = (An-A0)/n。

然而，從率失真的角度來考慮，最佳標量量化並不能達到最佳率失真編碼的要求，通常需要對量化後的資料進行繼續進行處理，如熵編碼等。

為了使量化後不再進行後處理而能逼近率失真函式的界，人們開始探討根據多個連續信源符號聯合編碼的方法，即向量量化技術。
假設X = {X1, X2, …, Xn}是信源的一個n維向量，它的取值範圍是n維空間中的一個區域Rn，一個k級的向量量化器就是X∈Rn到k個n維量化向量Y1, Y2, …, Y的對映函式Q(X)。對於任意Yi，i = 1, 2, …, k，指定一個n維的區域Ai，對於所有X∈Ai，有Q(X) = Yi。其中Ai稱為Yi的包腔，各量化向量稱為碼字，它們的集合稱為碼書。如果選擇的碼書和各包腔可以使平均失真最小，這時的向量量化稱為最佳向量量化。

4.1.5 率失真優化

率失真函式給出了信源編碼的資訊率極限，而率失真優化則研究如何達到該極限，即在給定資訊率上限Rc的前提下，尋找一種編碼方法使D最小化：

min{D(P)} s.t. R(P) ≤ Rc

其中，P表示一個信源編碼前後的轉移概率，代表某種編碼方法。

這是一個典型的有約束的非線性規劃問題，可以通過拉格朗日乘子法轉化為一個無約束的求極小值的問題：

min{D(P)+λ*R(P)}

這裡的λ與約束條件Rc息息相關，目標速率越大，則λ越小，當λ為零時，表示不限制目標速率，則只剩下min{D(P)}了。

實際的編碼過程不是數學推理過程，無需對上面的方程求解，只要確定了λ（這是個關鍵點），通過窮舉搜尋即可找到最佳的編碼方法。

4.2 影像

4.3 視訊

4.3.1 混合編碼系統

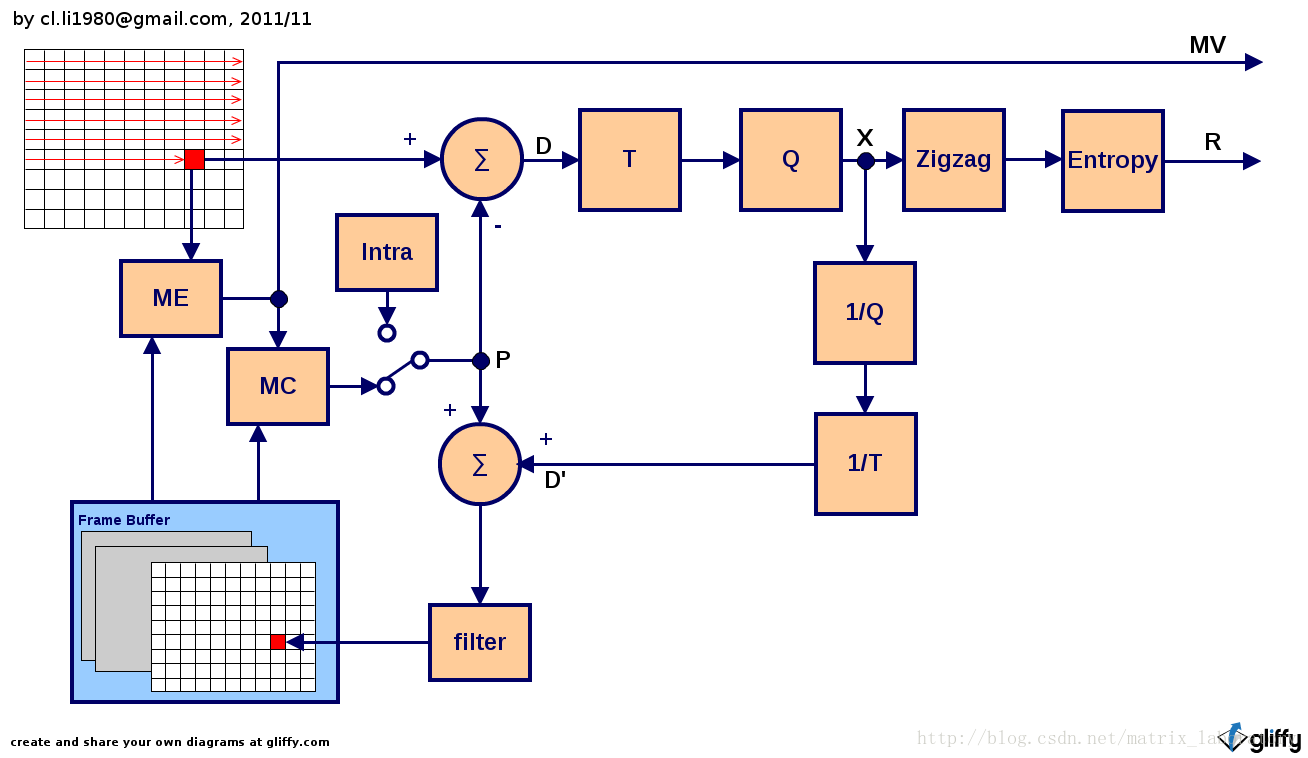
所謂混合指的是運動預測差分編碼和變換編碼的混合，其一般編碼原理由上圖給出，通常是以巨集塊為單位按照掃描順序進行編碼，當然也不排除基於某種大規模並行運算的編碼方法改掉這一方式。整個處理過程中，涉及到的資料包括：

• P: 預測值
• D: 差分值
• D’: 本地恢復的差分值
• X: 量化後的殘差變換系數
• R: 經過熵編碼的殘差變換系數

主要的處理模組包括：

4.3.1.1 ME：運動估計

這裡的運動估計指的是為待編碼巨集塊中的各個畫素點尋找最佳預測值的搜尋過程，找到的預測值位於某一幀已經編碼並重建的影像中，與被預測的畫素點在位置上存在偏差，這些偏差就叫作運動向量，它們和參考幀的位置共同作為運動估計過程的最終輸出物。

4.3.2.2 MC: 運動補償

運動補償也叫做運動補償預測，這一過程根據運動估計給出的運動向量和參考幀位置生成待編碼巨集塊各畫素點的預測值。由待編碼影像和經運動補償的參考影像逐點相減可生成一副差分影像，相對與自然影像，差分影像的動態範圍大大減小，從而更有力於後續的壓縮

4.3.2.3 T: 變換

通過對待編碼畫素與預測值的差值進行一個二維變換，有效地去除空間冗餘。

4.3.2.4 Q: 量化

變換系數的量化通過引入失真降低位元率。

4.2.3.5 1/T: 反變換

這一過程和下一過程的主要目的是生成本地重建影像。由於解碼器端無法獲取原始影像，為了防止誤差積累，需要在編碼器端複製解碼過程，使用解碼後的重建影像代替原始影像進行預測。

4.2.3.6 1/Q: 反量化

4.2.3.7 Zigzag: Z掃描

Z掃描可以將二維的殘差變換系數轉換為一維的序列，更有利於其後的熵編碼。

4.2.3.8 Entropy: 熵編碼

利用資料流內部的統計特性對一維的殘差變換系數進行無失真壓縮。

4.2.3.9 Filter: 環內濾波

環內濾波有兩個目的：其一是為了去除因變換產生的塊效應；其二是通過改善重建影像，使預測過程更有效。

4.2.3.10 Intra: 幀內預測

在某些情況下，無法獲得參考幀，或參考幀中的預測值與實際值的差距過大（比如視訊序列發生場景切換），則不採用已編碼重建影像中的畫素值作為預測值，而以當前影像中已編碼部分的畫素值作為預測值。

4.2.3.11 模式選擇

此外，編碼過程還隱含著一個模式選擇的模組，體現在上圖中就是決定幀內還是幀間的開關，而實際上除了這個的開關，其他諸如運動補償、幀內預測都要涉及到模式選擇，譬如基於多大的塊進行運動補償、使用哪一個參考幀等。

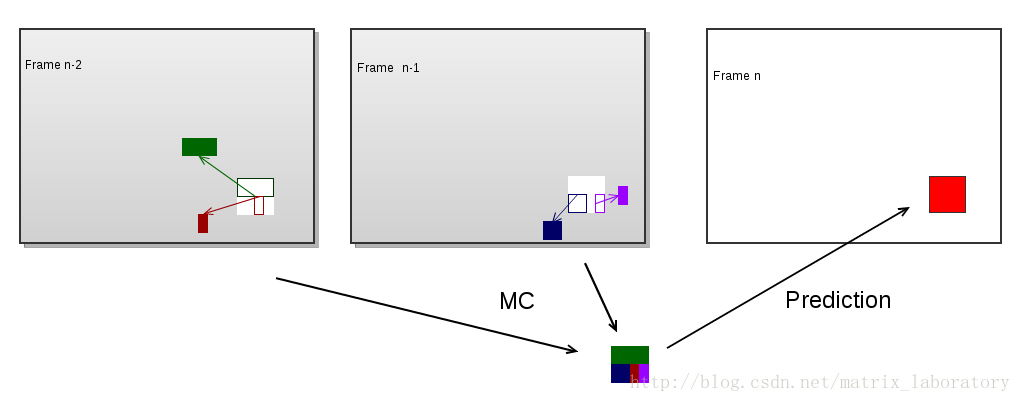
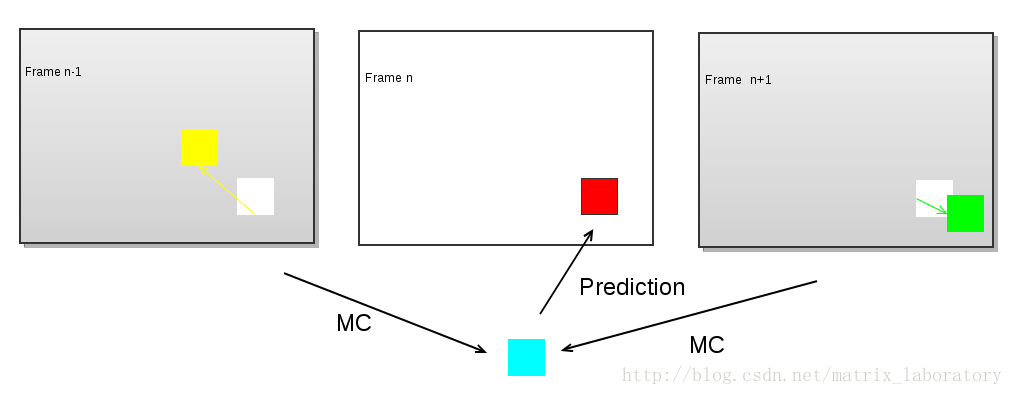
運動補償預測可以用下圖來表示

紅色部分為待編碼的巨集塊，彩色部分為利用運動補償由本地解碼的重構影像生成的預測值，而最終編碼的是紅色部分和彩色部分的差值。可以看出，為了完成該巨集塊的預測，需要四個運動向量和兩個參考幀。某些編碼技術如雙向預測及MPEG2中的Dual-Prime會令預測過程更加複雜，預測值需要由兩個經運動補償的預測值加權平均得到：