字串相似度演算法（編輯距離演算法 Levenshtein Distance）（轉）

在搞驗證碼識別的時候需要比較字元程式碼的相似度用到“編輯距離演算法”，關於原理和C#實現做個記錄。

據百度百科介紹：

編輯距離，又稱Levenshtein距離（也叫做Edit Distance），是指兩個字串之間，由一個轉成另一個所需的最少編輯操作次數，如果它們的距離越大，說明它們越是不同。許可的編輯操作包括將一個字元替換成另一個字元，插入一個字元，刪除一個字元。

　　例如將kitten一字轉成sitting：

　　sitten （k→s）

　　sittin （e→i）

　　sitting （→g）

　　俄羅斯科學家Vladimir Levenshtein在1965年提出這個概念。因此也叫Levenshtein Distance。

例如

• 如果str1="ivan"，str2="ivan"，那麼經過計算後等於 0。沒有經過轉換。相似度=1-0/Math.Max(str1.length,str2.length)=1
• 如果str1="ivan1"，str2="ivan2"，那麼經過計算後等於1。str1的"1"轉換"2"，轉換了一個字元，所以距離是1，相似度=1-1/Math.Max(str1.length,str2.length)=0.8

應用

　　DNA分析

　　拼字檢查

　　語音辨識

　　抄襲偵測

感謝大石頭在評論中給出一個很好的關於此方法應用的連線 補充在此：

小規模的字串近似搜尋，需求類似於搜尋引擎中輸入關鍵字，出現類似的結果列表，文章連線:【演算法】字串近似搜尋

演算法過程

1. str1或str2的長度為0返回另一個字串的長度。 if(str1.length==0) return str2.length; if(str2.length==0) return str1.length;
2. 初始化(n+1)*(m+1)的矩陣d，並讓第一行和列的值從0開始增長。
3. 掃描兩字串（n*m級的），如果：str1[i] == str2[j]，用temp記錄它，為0。否則temp記為1。然後在矩陣d[i,j]賦於d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp三者的最小值。
4. 掃描完後，返回矩陣的最後一個值d[n][m]即是它們的距離。

計算相似度公式：1-它們的距離/兩個字串長度的最大值。

為了直觀表現，我將兩個字串分別寫到行和列中，實際計算中不需要。我們用字串“ivan1”和“ivan2”舉例來看看矩陣中值的狀況：

1、第一行和第一列的值從0開始增長

		i	v	a	n	1
	0	1	2	3	4	5
i	1
v	2
a	3
n	4
2	5

 

2、i列值的產生 Matrix[i - 1, j] + 1 ; Matrix[i, j - 1] + 1   ;    Matrix[i - 1, j - 1] + t

		i	v	a	n	1
	0+t=0	1+1=2	2	3	4	5
i	1+1=2	取三者最小值=0
v	2	依次類推：1
a	3	2
n	4	3
2	5	4

 

3、V列值的產生

		i	v	a	n	1
	0	1	2
i	1	0	1
v	2	1	0
a	3	2	1
n	4	3	2
2	5	4	3

 

依次類推直到矩陣全部生成

		i	v	a	n	1
	0	1	2	3	4	5
i	1	0	1	2	3	4
v	2	1	0	1	2	3
a	3	2	1	0	1	2
n	4	3	2	1	0	1
2	5	4	3	2	1	1

 

最後得到它們的距離=1

相似度：1-1/Math.Max(“ivan1”.length,“ivan2”.length) =0.8

 

演算法用C#實現

public class LevenshteinDistance
    {
        /// <summary>
        /// 取最小的一位數
        /// </summary>
        /// <param name="first"></param>
        /// <param name="second"></param>
        /// <param name="third"></param>
        /// <returns></returns>
        private int LowerOfThree(int first, int second, int third)
        {
            int min = Math.Min(first, second);
            return Math.Min(min, third);
        }

        private int Levenshtein_Distance(string str1, string str2)
        {
            int[,] Matrix;
            int n = str1.Length;
            int m = str2.Length;

            int temp = 0;
            char ch1;
            char ch2;
            int i = 0;
            int j = 0;
            if (n == 0)
            {
                return m;
            }
            if (m == 0)
            {

                return n;
            }
            Matrix = new int[n + 1, m + 1];

            for (i = 0; i <= n; i++)
            {
                //初始化第一列
                Matrix[i, 0] = i;
            }

            for (j = 0; j <= m; j++)
            {
                //初始化第一行
                Matrix[0, j] = j;
            }

            for (i = 1; i <= n; i++)
            {
                ch1 = str1[i - 1];
                for (j = 1; j <= m; j++)
                {
                    ch2 = str2[j - 1];
                    if (ch1.Equals(ch2))
                    {
                        temp = 0;
                    }
                    else
                    {
                        temp = 1;
                    }
                    Matrix[i, j] = LowerOfThree(Matrix[i - 1, j] + 1, Matrix[i, j - 1] + 1, Matrix[i - 1, j - 1] + temp);
                }
            }
 	   for (i = 0; i <= n; i++)
            {
                for (j = 0; j <= m; j++)
                {
                    Console.Write(" {0} ", Matrix[i, j]);
                }
                Console.WriteLine("");
            }
      
            return Matrix[n, m];
        }

        /// <summary>
        /// 計算字串相似度
        /// </summary>
        /// <param name="str1"></param>
        /// <param name="str2"></param>
        /// <returns></returns>
        public decimal LevenshteinDistancePercent(string str1, string str2)
        {
            //int maxLenth = str1.Length > str2.Length ? str1.Length : str2.Length;
            int val = Levenshtein_Distance(str1, str2);
            return 1 - (decimal)val / Math.Max(str1.Length, str2.Length);
        }
    }

 

1	<strong>呼叫</strong>

static void Main(string[] args)
        {
            string str1 = "ivan1";
            string str2 = "ivan2";
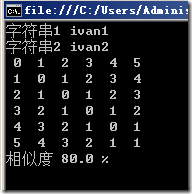
            Console.WriteLine("字串1 {0}", str1);

            Console.WriteLine("字串2 {0}", str2);

            Console.WriteLine("相似度 {0} %", new LevenshteinDistance().LevenshteinDistancePercent(str1, str2) * 100);          
            Console.ReadLine();
        }

 

1	<strong>結果</strong>

http://www.cnblogs.com/ivanyb/archive/2011/11/25/2263356.html