Gerald bought two very rare paintings at the Sotheby's auction and he now wants to hang them on the wall. For that he bought a special board to attach it to the wall and place the paintings on the board. The board has shape of ana1 × b1 rectangle, the paintings have shape of aa2 × b2 anda3 × b3 rectangles.
Since the paintings are painted in the style of abstract art, it does not matter exactly how they will be rotated, but still, one side of both the board, and each of the paintings must be parallel to the floor. The paintings can touch each other and the edges of the board, but can not overlap or go beyond the edge of the board. Gerald asks whether it is possible to place the paintings on the board, or is the board he bought not large enough?
The first line contains two space-separated numbers a1 andb1 — the sides of the board. Next two lines contain numbersa2, b2, a3 andb3 — the sides of the paintings. All numbersai, bi in the input are integers and fit into the range from1 to 1000.
If the paintings can be placed on the wall, print "YES" (without the quotes), and if they cannot, print "NO" (without the quotes).
3 2 1 3 2 1
YES
5 5 3 3 3 3
NO
4 2 2 3 1 2
YES
That's how we can place the pictures in the first test:
And that's how we can do it in the third one.
題目要求把兩幅畫放到一塊黑板上，要求兩幅畫不重疊不越界。所以能夠先將一幅畫放上去。在剩下的區域裡面能夠有兩個位置去放，暴力列舉各種情況就可以。當中要注意第一幅畫本身是否能放上去。
#include<stdio.h>
#include<string.h>
int main()
{
int a1,b1,a2,b2,a3,b3,i,j,k;
while(scanf("%d%d",&a1,&b1)!=EOF)
{
scanf("%d%d%d%d",&a2,&b2,&a3,&b3);
int x1=a1-a2;
int x2=a1-b2;
int y1=b1-b2;
int y2=b1-a2;
int f=0;
if((x1>=a3&&b1>=b3&&b1>=b2)||(x1>=b3&&b1>=a3&&b1>=b2)){
printf("YES\n");continue;
}
if((y1>=b3&&a1>=a3&&a1>=a2)||(y1>=a3&&a1>=b3&&a1>=a2)){
printf("YES\n");continue;
}
if((x2>=a3&&b1>=b3&&b1>=a2)||(x2>=b3&&b1>=a3&&b1>=a2)){
printf("YES\n");continue;
}
if((y2>=a3&&a1>=b3&&a1>=b2)||(y2>=b3&&a1>=a3&a1>=b2)){
printf("YES\n");continue;
}
else printf("NO\n");
}
}Gerald got a very curious hexagon for his birthday. The boy found out that all the angles of the hexagon are equal to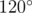
.
Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.
He painted a few lines, parallel to the sides of the hexagon. The lines split the hexagon into regular triangles with sides of 1 centimeter. Now Gerald wonders how many triangles he has got. But there were so many of them that Gerald lost the track of his counting. Help the boy count the triangles.
The first and the single line of the input contains 6 space-separated integersa1, a2, a3, a4, a5 anda6 (1 ≤ ai ≤ 1000) — the lengths of the sides of the hexagons in centimeters in the clockwise order. It is guaranteed that the hexagon with the indicated properties and the exactly such sides exists.
Print a single integer — the number of triangles with the sides of one 1 centimeter, into which the hexagon is split.
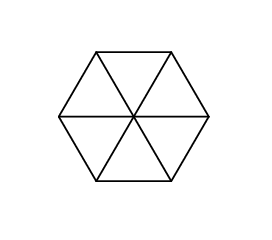
1 1 1 1 1 1
6
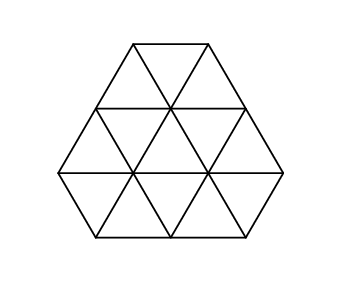
1 2 1 2 1 2
13
This is what Gerald's hexagon looks like in the first sample:
And that's what it looks like in the second sample:
假設畫一繪圖就能發現，假設將圖形補成一個大的等腰三角形，那麼小三角形的數目就是左側（或右側）三條邊加起來以後的平方。由於對於一個邊長為n 的等腰三角形來說。裡面的小三角形是有n^2個的。所以題目中要求的三角形數量就是大的減去邊上三個小的。
#include<stdio.h>
int s(int i)
{
return i*i;
}
int main()
{
int a[6],ans;
while(~scanf("%d",&a[0]))
{
for(int i=1;i<6;i++)
scanf("%d",&a[i]);
ans=a[0]+a[1]+a[2];
printf("%d\n",s(ans)-s(a[0])-s(a[2])-s(a[4]));
}
}Today on a lecture about strings Gerald learned a new definition of string equivalency. Two strings a and b of equal length are called equivalent in one of the two cases:
- They are equal.
- If we split string a into two halves of the same size
a1 and
a2, and string
b into two halves of the same size b1 and
b2, then one of the following is correct:
- a1 is equivalent to b1, and a2 is equivalent to b2
- a1 is equivalent to b2, and a2 is equivalent to b1
As a home task, the teacher gave two strings to his students and asked to determine if they are equivalent.
Gerald has already completed this home task. Now it's your turn!
The first two lines of the input contain two strings given by the teacher. Each of them has the length from 1 to 200 000 and consists of lowercase English letters. The strings have the same length.
Print "YES" (without the quotes), if these two strings are equivalent, and "NO" (without the quotes) otherwise.
aaba abaa
YES
aabb abab
NO
In the first sample you should split the first string into strings "aa" and "ba", the second one — into strings "ab" and "aa". "aa" is equivalent to "aa"; "ab" is equivalent to "ba" as "ab" = "a" + "b", "ba" = "b" + "a".
In the second sample the first string can be splitted into strings "aa" and "bb", that are equivalent only to themselves. That's why string "aabb" is equivalent only to itself and to string "bbaa".
- They are equal.
- If we split string a into two halves of the same size
a1 and
a2, and string
b into two halves of the same size b1 and
b2, then one of the following is correct:
- a1 is equivalent to b1, and a2 is equivalent to b2
- a1 is equivalent to b2, and a2 is equivalent to b1
因為我拆分字串的時候一定要等分，所以假設字串是奇數的，直接strcmp比較就可以。
假設是偶數，那麼久要拆分了。這裡注意，我能夠一直拆分直到被拆分的字串變成奇數。
拆分過程中，假設有一組滿足條件。那就滿足條件了。所以能夠呼叫遞迴函式。
#include<stdio.h>
#include<string.h>
char a[200005],b[200005];
bool panduan(char * s1,char *s2,int l)
{
if(strncmp(s1,s2,l)==0)return true; //這裡用了strncmp函式。即比較s1,s2前l個字元是否同樣。
if(l%2==1)return false;
int i,j;
/* char s3[100005],s4[100005];
char s5[100005],s6[100005];
for(i=0;i<l/2;i++)
{
s3[i]=s1[i];
s5[i]=s2[i];
}
for(i=l/2;i<l;i++)
{
s4[i-l/2]=s1[i];
s6[i-l/2]=s2[i];
}
*/ //這裡的部分是我第一次寫的時候T的程式碼，沒實用strncmp函式。應該是由於遞迴呼叫過多，for迴圈用的也特別多。if(panduan(s1,s2+l/2,l/2)&&panduan(s1+l/2,s2,l/2))return true; if(panduan(s1,s2,l/2)&&panduan(s1+l/2,s2+l/2,l/2))return true; //注意這一行與上一行這題裡面換不了，一換就T了。預計是資料問題。
//假設實在要換，能夠手寫strncmp函式。可能能夠過，我沒試過。
return false; } int main() { int i,j,k,l; while(scanf("%s%s",a,b)!=EOF) { l=strlen(a); if(l%2==1){ if(strcmp(a,b)==0)printf("YES\n"); else printf("NO\n"); } else { if(panduan(a,b,strlen(a)))printf("YES\n"); else printf("NO\n"); } } }