形態學影像處理(二)
本文主要包括以下內容
- 二值形態學的經典應用, 細化和畫素化, 以及凸殼
- 灰度影像的形態學運算, 包括灰度腐蝕、灰度膨脹、灰度開和灰度閉
- 本章的典型案例分析
- 在人臉區域性影像中定位嘴的中心
- 顯微鏡下影像的細菌計數
- 利用頂帽變換(top-hat)技術解決光照不均問題
細化演算法
“骨架”是指一副影像的骨髓部分,它描述物體的幾何形狀和拓撲結構,是重要的影像描繪子之一,計算骨架的過程一般稱為“細化”或“骨架化”,在包括文字識別、工業零件形狀識別以及印刷電路板自動檢測在內的很多應用中,細化過程都發揮著關鍵作用。通常,對我們感興趣的目標物體進行細化有助於突出目標的形狀特點和拓撲結構並且減少冗餘的資訊量。


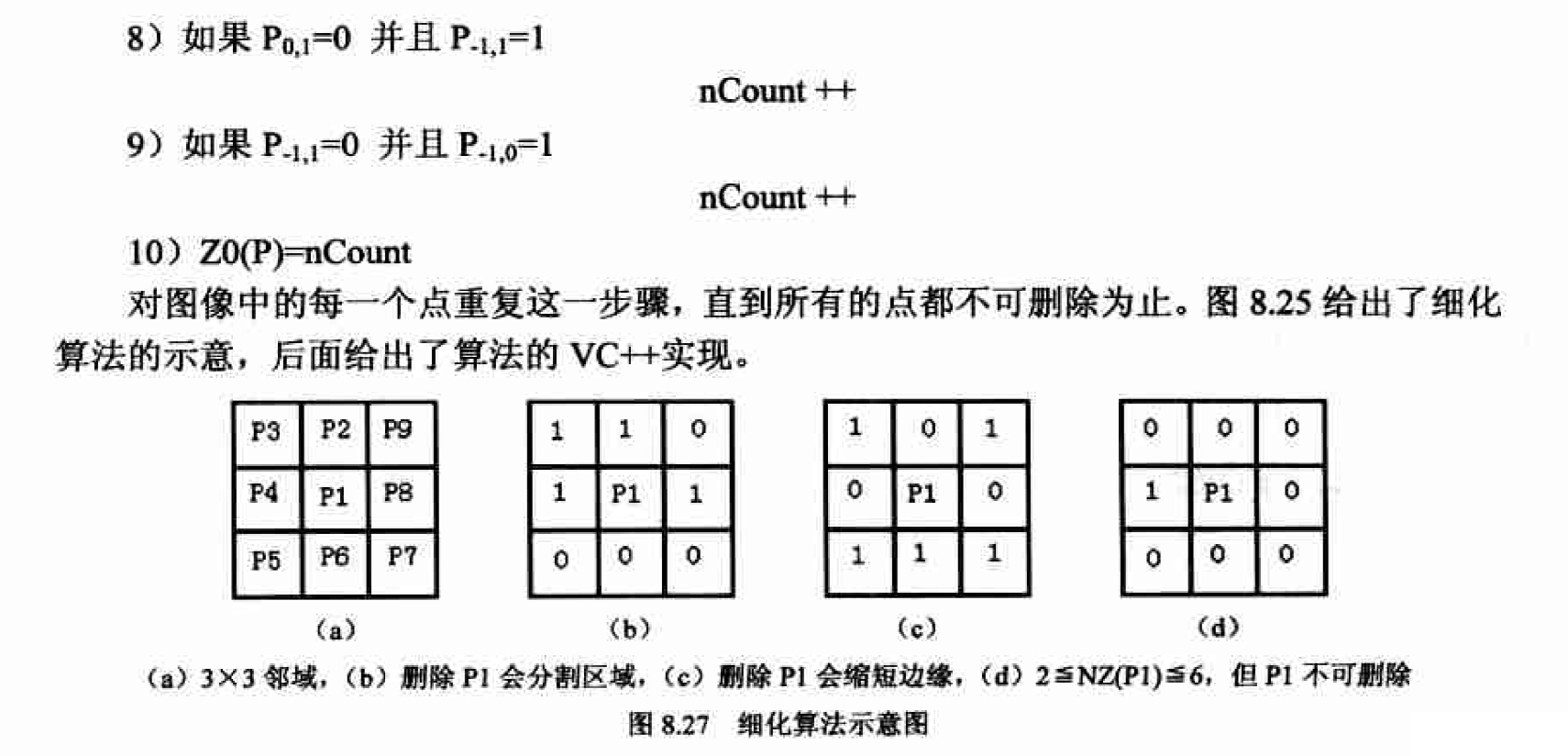
畫素化演算法
細化適用於和物體拓撲結構或形狀有關的應用, 如前述的手寫字元識別。 但有時我們關心的是目標物件是否存在、 它們的位置關係, 或者個數, 這時在預處理中加入畫素化步驟會給後續的影像分析帶來極大的方便
理論基礎
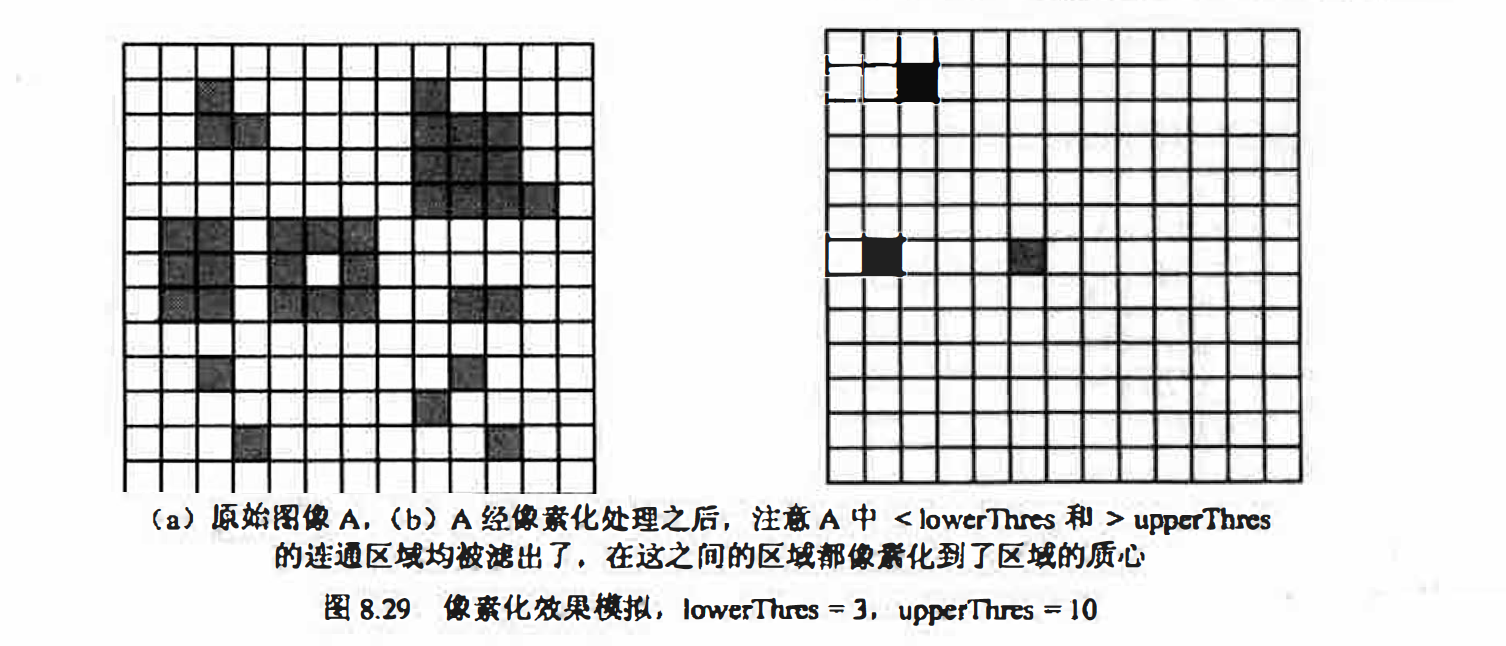
畫素化操作首先需找到二值影像中所有的連通區域, 然後用這些區域的質心作為這些連通區域的代表, 即將1個連通區域畫素化為位於區域質心位置的1個畫素。
有時還可以進一步引入一個低閥值lowerThres和一個高闕值highThres來指出影像中我們感興趣的物件連通數(連通分量中的畫素數目)的大致範圍, 從而只畫素化影像中大小介於lowerThres和upperThres之間的連通區域, 而連通數低於lowerThres或高於upperThres的物件都將被濾除, 這就相當於使用演算法的同時具有了過濾噪聲的能力。如圖8.29 所示。
凸殼
如果連線物體A內任意兩點的直線段都在淫的內部,則稱d是凸的。任意物體A的凸亮H是包含A的最小凸物體。
我們總是希望畫素化演算法能夠找到物體的質心來代表讀物體,但在實際中,可能由於光照不均等原因導致影像在二值化後,物體本身形狀發生缺損,畫素化演算法就無法找到物體真正的質心。此時可適當地進行凸殼處理,彌補凹損,演算法會找到包含原始形狀的最小凸多邊形,如下圖8.30所示.
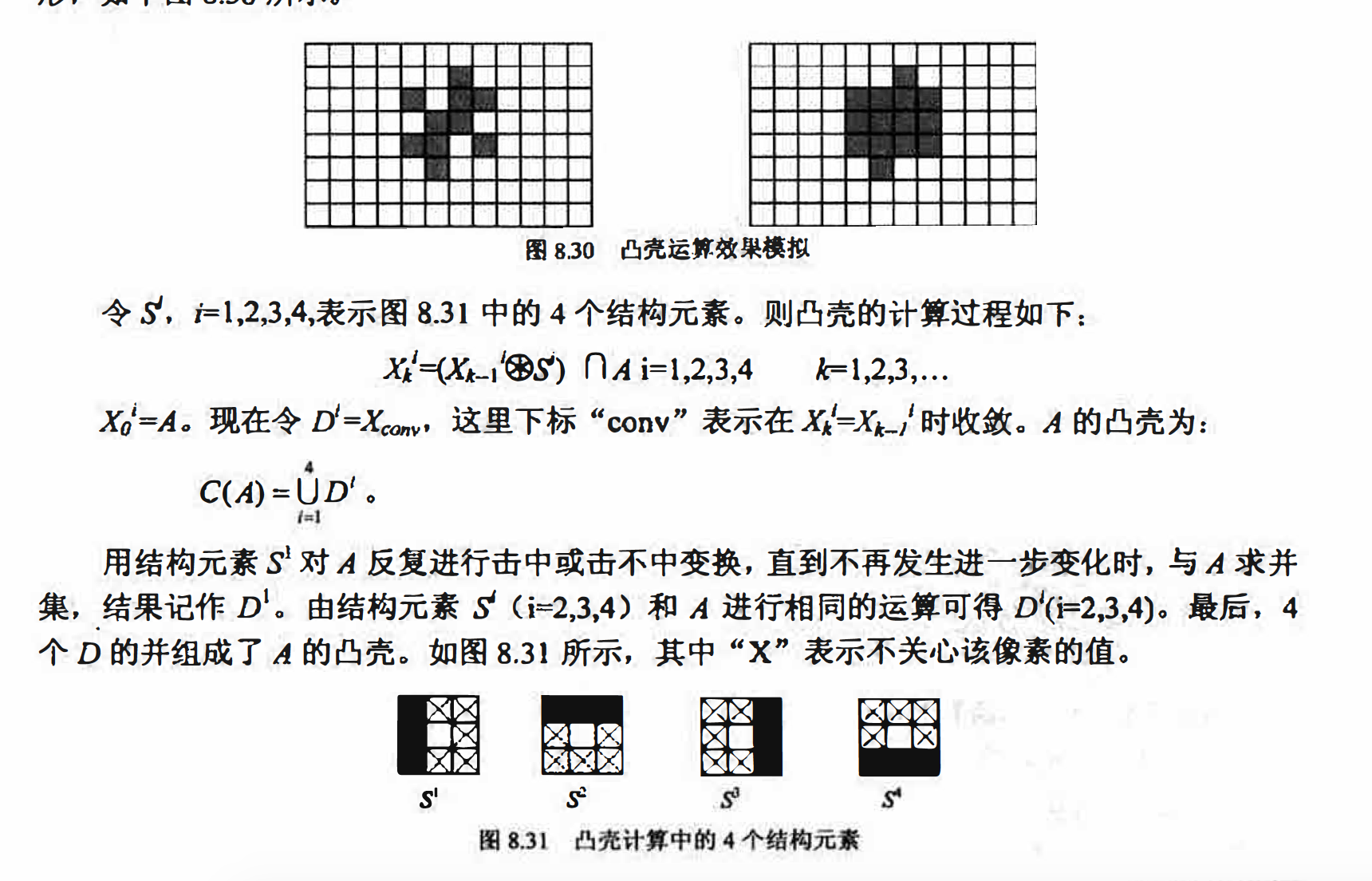
為確保在上述生長過程中凸殼不會大幅超出凸性所需的最小尺寸, 可以限制其生長以便凸殼不會超出初始時包含物體A的最小矩形.
bwmorph函式
本章的很多形態學操作都可由IPT函式bwmorph實現, 該函式的呼叫語法為:
Iout = bwmorph(I,operation,n);
operation是一個指定操作型別的字串, 常用的合法取位如在8.2 所示
灰度影像中的基本形態學運算
本節就們把二值影像的形態學處理擴充套件到灰度影像的基本操作, 包括灰度膨脹、灰皮腐蝕、灰度開和灰皮閉。此外, 8.4.4 小節還將介紹一個灰度形態學的經典應用一一頂帽變換(top-hat), 用以解決影像的光照不均問題.
灰度膨脹及其實現

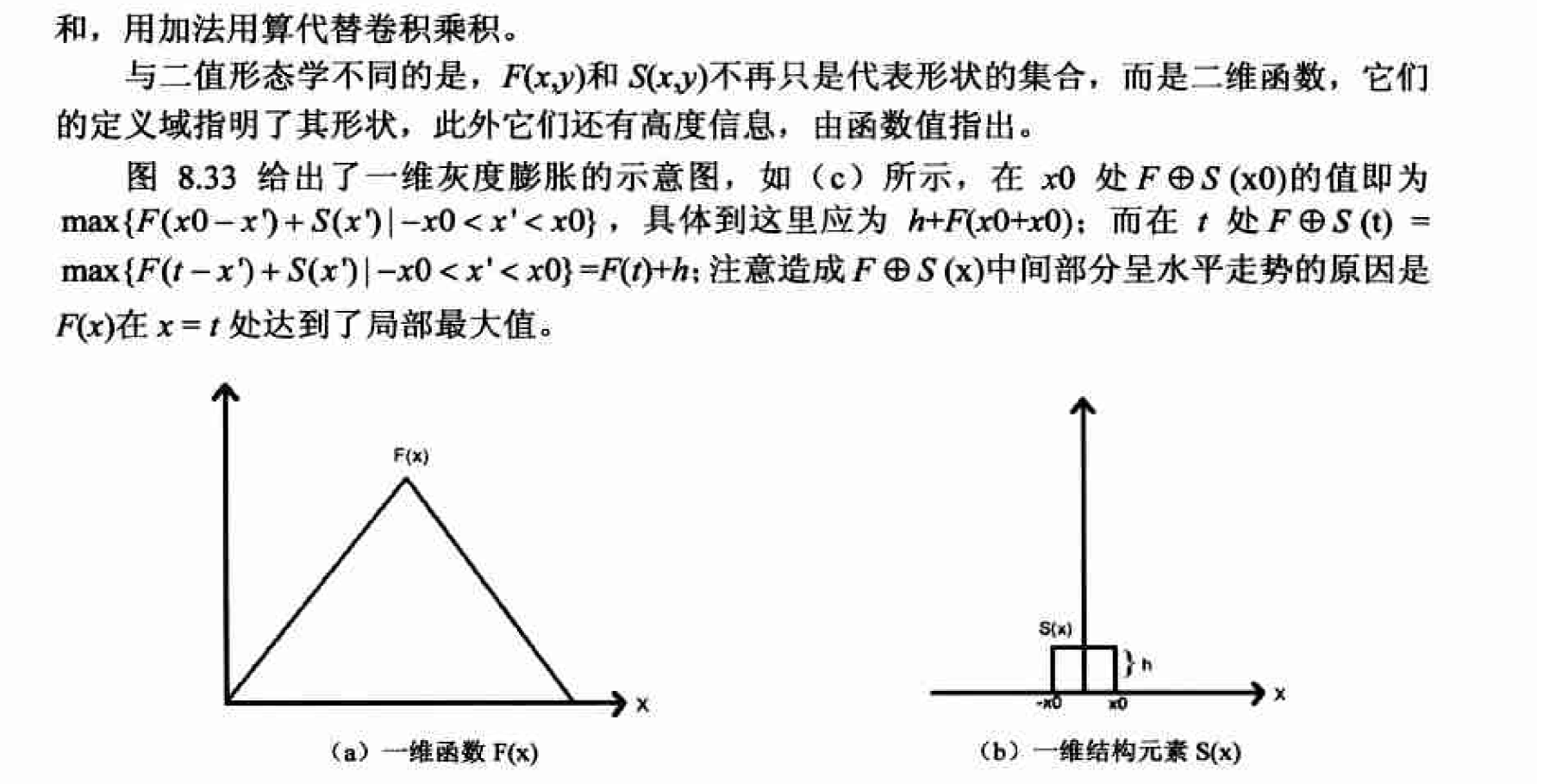
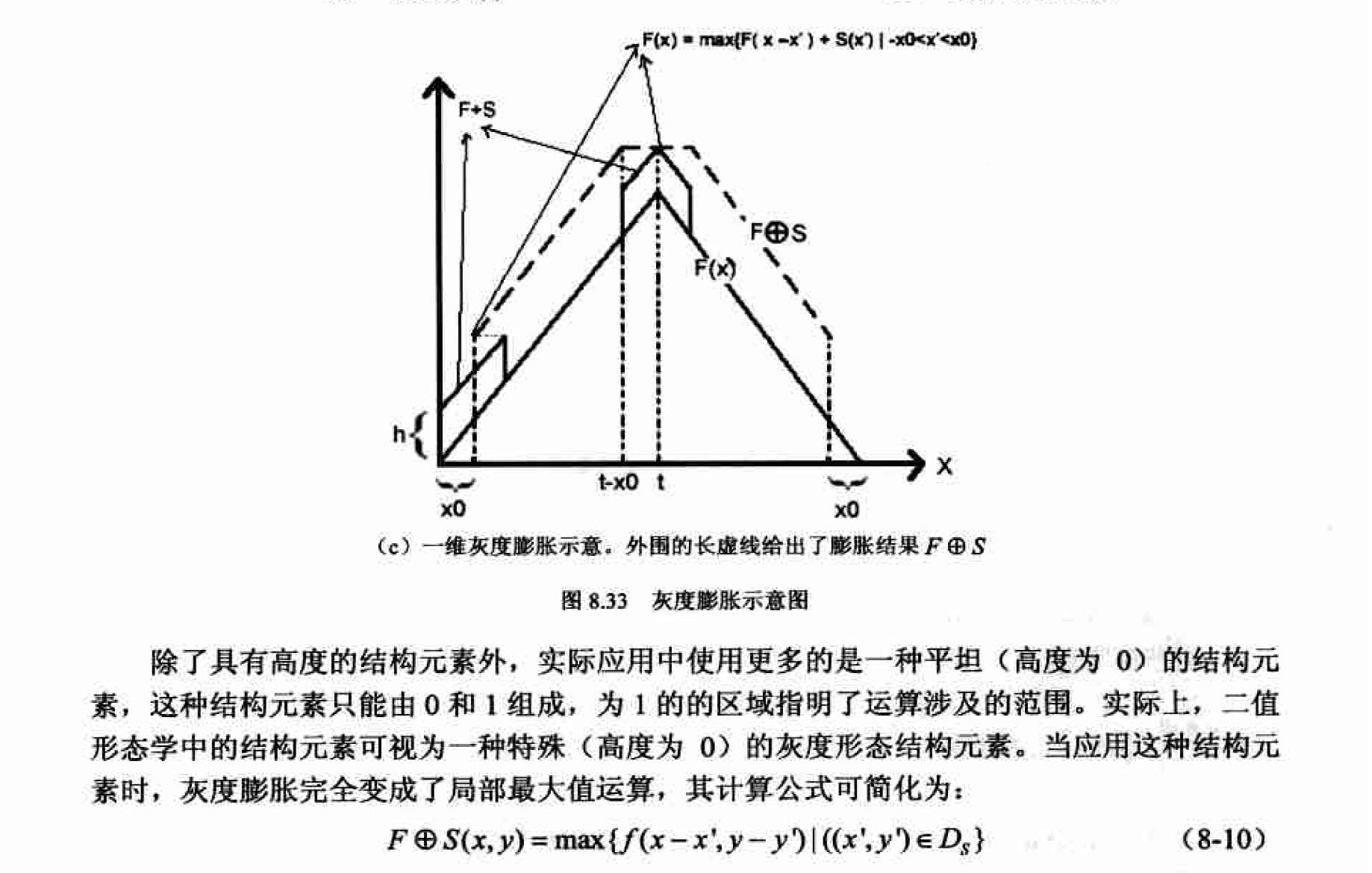
matlab實現
只要以灰度影像和相應的灰度膨脹結構元素為引數呼叫imdilate函式即可實現灰度膨脹,平坦結構元素的建立方法與二值形態學中相同:而非平坦結構元素也可通過 strel函式以如下方式建立。
SE = strel(NHOOD,HEIGHT);
NHOOD 為指明結構元素定義域的矩陣, 只能由0和1 組成.
HEIGHT 是一個與NHOOD 具有相同尺寸的矩陣, 指出了對應於NHOOD 中每個元素的高度.
f = [0 1 2 3 4 5 4 3 2 1 0];
figure,h_f = plot(f);
seFlat = strel([1 1 1]);
fd1 = imdilate(f,seFlat);
hold on,h_fd1 = plot(fd1,'-ro');
axis([1 11 0 8]);
setHeight = strel([1 1 1],[1 1 1]);
fd2 = imdilate(f,setHeight);
hold on,h_fd2= plot(fd2,'-g*');
legend('原灰度1維函式f','使用平坦結構元素膨脹','使用高度為1有結構元素膨脹元素膨脹後');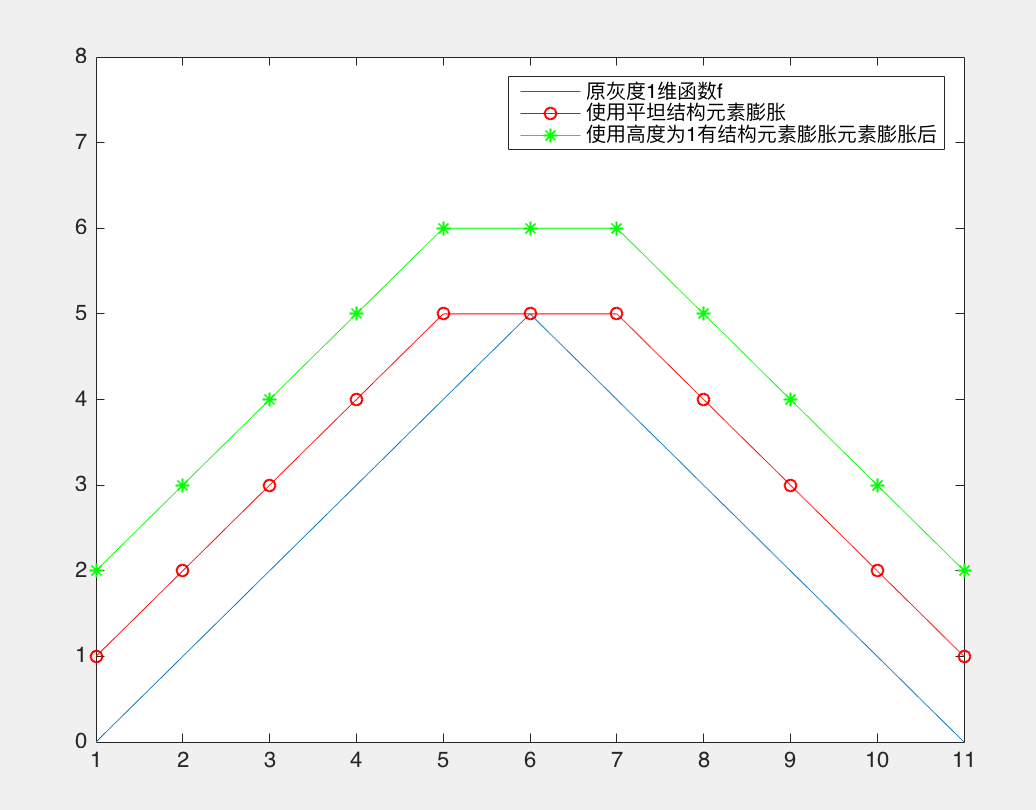
灰度腐蝕及其實現

與二值形態學不同的是,f(x,y)和 S(x,y)不再是隻代表形狀的集合,而是二維函式,它們的定義域指明瞭其形狀, 它們的值指出了高度資訊。
f = [0 1 2 3 4 5 4 3 2 1 0];
figure,h_f = plot(f);
seFlat = strel([1 1 1]);
fe1 = imerode(f,seFlat);
hold on,h_fe1 = plot(fe1,'ro');
axis([1 11 0 8]);
seHeight = strel([1 1 1],[1 1 1]);
fe2 = imerode(f,seHeight);
hold on,h_fe2=plot(fe2,'-g*');
legend('原灰度1維函式f','使用平坦結構元素腐蝕','使用高度為1有結構元素膨脹元素腐蝕後');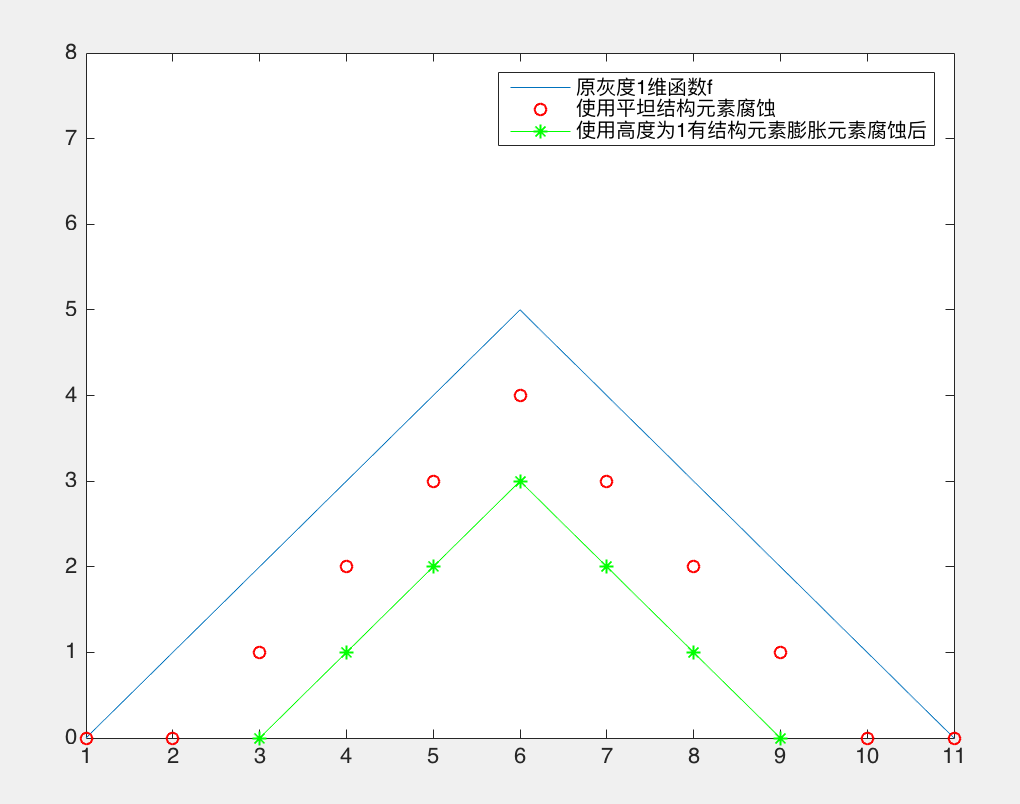
灰度膨脹和灰度腐蝕的效果比較
I = imread('lena.bmp');
seHeight=strel(ones(3,3),ones(3,3));
Idi1= imdilate(I,seHeight);
Iero = imerode(I,seHeight);
subplot(1,3,1),imshow(I);
subplot(1,3,2),imshow(Idi1);
subplot(1,3,3),imshow(Iero);
我們看到在結構元素的值均大於零的情況下, 灰度膨脹的輸出影像總體上比輸入影像更亮,這是區域性最大值運算作用的結果。此外原影像中一些能夠包含於結構元素的暗細節〈如
一部分帽子的槽皺和尾穗)被完全消除, 其餘的大部分暗部細節也都得到了一定程度上的減少。而灰度腐蝕的作用正好相反, 輸出影像比輸入影像更暗, 如果輸入影像中的亮部細節比結構元素小, 則亮度會得到削弱。
灰度開、 閉運算及其實現
與二值形態學類似,我們可以在灰度腐蝕和膨脹的基礎上定義灰度開和閉運算.灰度開運算就是先灰度腐蝕後灰度膨脹,而灰度閉運算則是先灰度膨脹後灰度腐蝕,下面分別給出定義:

這一過程: (a)為影像中的一條水平畫素線:(b)和(d)分別給出了球緊貼著該畫素線的下側和上側被動的情況:而(c)和(e)則展示了滾動過程中球的最高點形成的曲線,它們分別是開、閉運算的結果。
Matlab實現
使用imopen和imdilate同樣可以對灰度影像進行開、閉運算, 用法與灰度腐蝕和膨脹類似, 這裡不再贅述,在實際應用中, 開操作常常用於去除那些相對於結構元素s而言較小的高灰度區域〈球體滾不上去〉,而對於較大的亮區域影響不大〈球體可以滾上去〉。雖然首先進行的灰度腐蝕
會在去除影像細節的同時使得整體灰度下降, 但隨後的灰度膨脹又會增強影像的整體亮度,因此影像的整體灰度基本保持不變:而閉操作常用於去除影像中的暗細節部分, 而相對地保留高灰度部分不受影響.
頂帽交換(top-hat)及其實現
作為灰度形態學的重要應用之一, 這裡學習一種非均勻光照問題的解決方案一一頂帽變換技術(top-hat).影像f的頂帽變換h定義為影像f與影像f的開運算之差, 可表示為:
h = f -(f*s)

I = imread('rice.png');
subplot(2,4,1),imshow(I,[]);
thresh = graythresh(I);
Ibw = im2bw(I,thresh);
subplot(2,4,2),imshow(Ibw,[]);
subplot(2,4,3),surf(double(I(1:8:end,1:8:end))),zlim([0 255]),colormap;
bg = imopen(I,strel('disk',15));
subplot(2,4,4),surf(double(bg(1:8:end,1:8:end))),zlim([0 255]),colormap;
Itophat = imsubtract(I,bg);
subplot(2,4,5),imshow(Itophat);
subplot(2,4,6),surf(double(Itophat(1:8:end,1:8:end))),zlim([0 255]);
I2 = imadjust(Itophat);
subplot(2,4,7),imshow(I2);
thresh2 = graythresh(I2);
Ibw2 = im2bw(I2,thresh2);
subplot(2,4,8),imshow(Ibw2);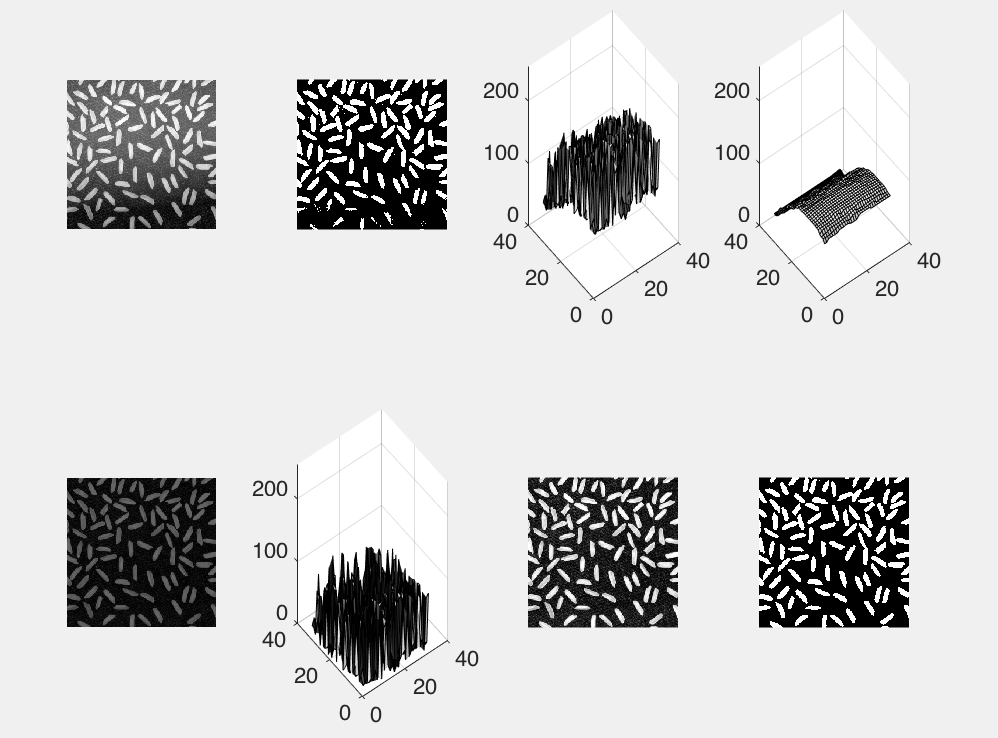
相關文章
- 形態學影像處理
- Python 影像處理 OpenCV (9):影像處理形態學開運算、閉運算以及梯度運算PythonOpenCV梯度
- Python 影像處理 OpenCV (10):影像處理形態學之頂帽運算與黑帽運算PythonOpenCV
- Python影像處理丨三種實現影像形態學轉化運算模式Python模式
- 深度學習之影像處理與分析(二)深度學習
- OpenCV與影像處理學習二——影像基礎知識(下)OpenCV
- 精通Python自然語言處理 3 :形態學Python自然語言處理
- C#開發PACS醫學影像處理系統(十二):繪圖處理之圖形標記C#繪圖
- 影像處理--影像特效特效
- webgl 影像處理2---影像畫素處理Web
- Python影像處理丨5種影像處理特效Python特效
- 影像預處理
- 醫學影像預處理之裁減
- 醫學影像預處理之標註
- Python 影像處理 OpenCV (6):影像的閾值處理PythonOpenCV
- Python 影像處理 OpenCV (7):影像平滑(濾波)處理PythonOpenCV
- 影像處理技術(二)濾波去噪(上)
- 數字影像處理學習筆記(1)——傅立葉變換在影像處理中的應用筆記
- 【數字影像處理】影像形態學演算法C語言實現(影像卷積,膨脹,腐蝕,開運算,閉運算,頂帽,黑帽,雕版,銳化)演算法C語言卷積
- 樹形結構的處理——組合模式(二)模式
- 前端影像處理指南前端
- 影像處理_切邊
- 影像預處理方法
- 影像輪廓處理
- 紅外影像處理
- 影像處理案例03
- OpenCV(影像NaN處理)OpenCVNaN
- C#處理醫學影像(二):基於Hessian矩陣的醫學影像增強與窗寬窗位C#矩陣
- 使用matlab對影像進行二值化處理Matlab
- 跟我學Python影像處理丨獲取影像屬性、興趣ROI區域及通道處理Python
- 圖形學之紋理後續/WebGL多紋理處理Web
- Windows批處理學習(二)——批處理(3)薦Windows
- 醫學影像處理中的資料讀寫
- OpenCV影像處理學習筆記-Day1OpenCV筆記
- 計算機視覺實戰的深度學習實戰二:影像預處理計算機視覺深度學習
- 影像行畫素處理
- 遙感影像處理流程
- 影像處理之骨架提取