Manacher演算法

演算法總結第三彈 manacher演算法，前面講了兩個字串相演算法——kmp和擴充kmp，這次來還是來總結一個字串演算法，manacher演算法，我習慣叫他 “馬拉車”演算法。

相對於前面介紹的兩個演算法，Manacher演算法的應用範圍要狹窄得多，但是它的思想和擴充kmp演算法有很多共通支出，所以在這裡介紹一下。Manacher演算法是查詢一個字串的最長迴文子串的線性演算法。

在介紹演算法之前，首先介紹一下什麼是迴文串，所謂迴文串，簡單來說就是正著讀和反著讀都是一樣的字串，比如abba，noon等等，一個字串的最長迴文子串即為這個字串的子串中，是迴文串的最長的那個。

計算字串的最長迴文字串最簡單的演算法就是列舉該字串的每一個子串，並且判斷這個子串是否為迴文串，這個演算法的時間複雜度為O(n^3)的，顯然無法令人滿意，稍微優化的一個演算法是列舉迴文串的中點，這裡要分為兩種情況，一種是迴文串長度是奇數的情況，另一種是迴文串長度是偶數的情況，列舉中點再判斷是否是迴文串，這樣能把演算法的時間複雜度降為O(n^2)，但是當n比較大的時候仍然無法令人滿意，Manacher演算法可以線上性時間複雜度內求出一個字串的最長迴文字串，達到了理論上的下界。

1.Manacher演算法原理與實現

下面介紹Manacher演算法的原理與步驟。

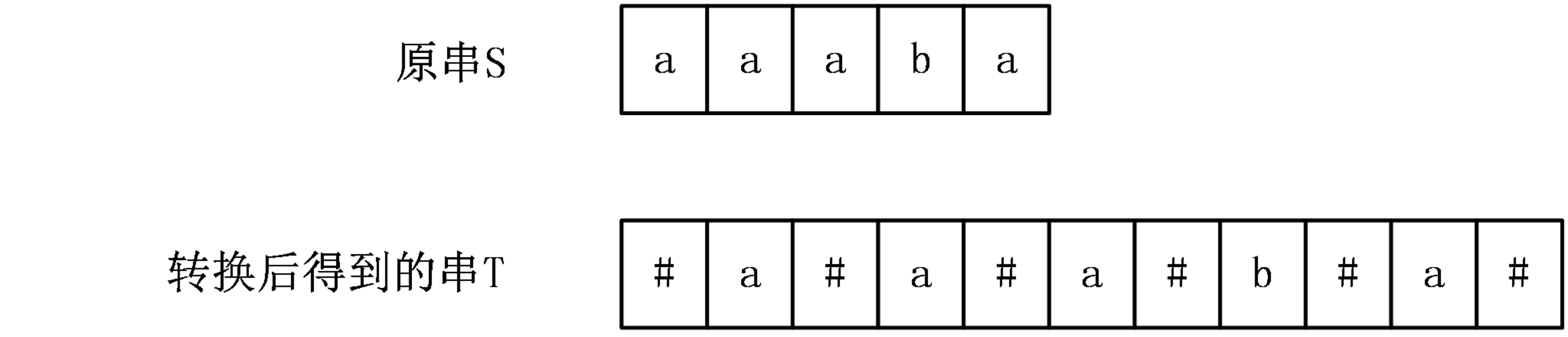
首先，Manacher演算法提供了一種巧妙地辦法，將長度為奇數的迴文串和長度為偶數的迴文串一起考慮，具體做法是，在原字串的每個相鄰兩個字元中間插入一個分隔符，同時在首尾也要新增一個分隔符，分隔符的要求是不在原串中出現，一般情況下可以用#號。下面舉一個例子：

（1）Len陣列簡介與性質

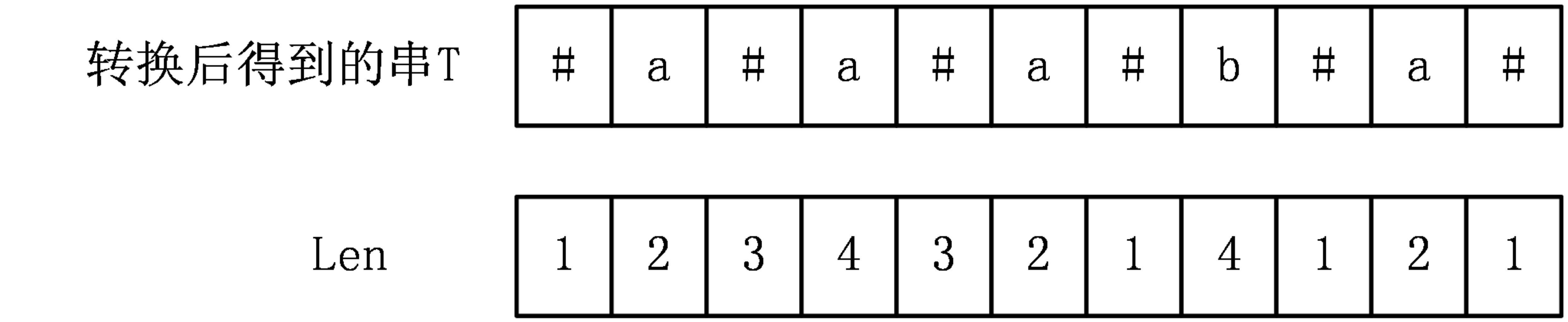
Manacher演算法用一個輔助陣列Len[i]表示以字元T[i]為中心的最長迴文字串的最右字元到T[i]的長度，比如以T[i]為中心的最長迴文字串是T[l,r],那麼Len[i]=r-i+1。

對於上面的例子，可以得出Len[i]陣列為:

Len陣列有一個性質，那就是Len[i]-1就是該回文子串在原字串S中的長度，至於證明，首先在轉換得到的字串T中，所有的迴文字串的長度都為奇數，那麼對於以T[i]為中心的最長迴文字串，其長度就為2*Len[i]-1,經過觀察可知，T中所有的迴文子串，其中分隔符的數量一定比其他字元的數量多1，也就是有Len[i]個分隔符，剩下Len[i]-1個字元來自原字串，所以該回文串在原字串中的長度就為Len[i]-1。

有了這個性質，那麼原問題就轉化為求所有的Len[i]。下面介紹如何線上性時間複雜度內求出所有的Len。

（2）Len陣列的計算

首先從左往右依次計算Len[i]，當計算Len[i]時，Len[j](0<=j<i)已經計算完畢。設P為之前計算中最長迴文子串的右端點的最大值，並且設取得這個最大值的位置為po，分兩種情況：

第一種情況：i<=P

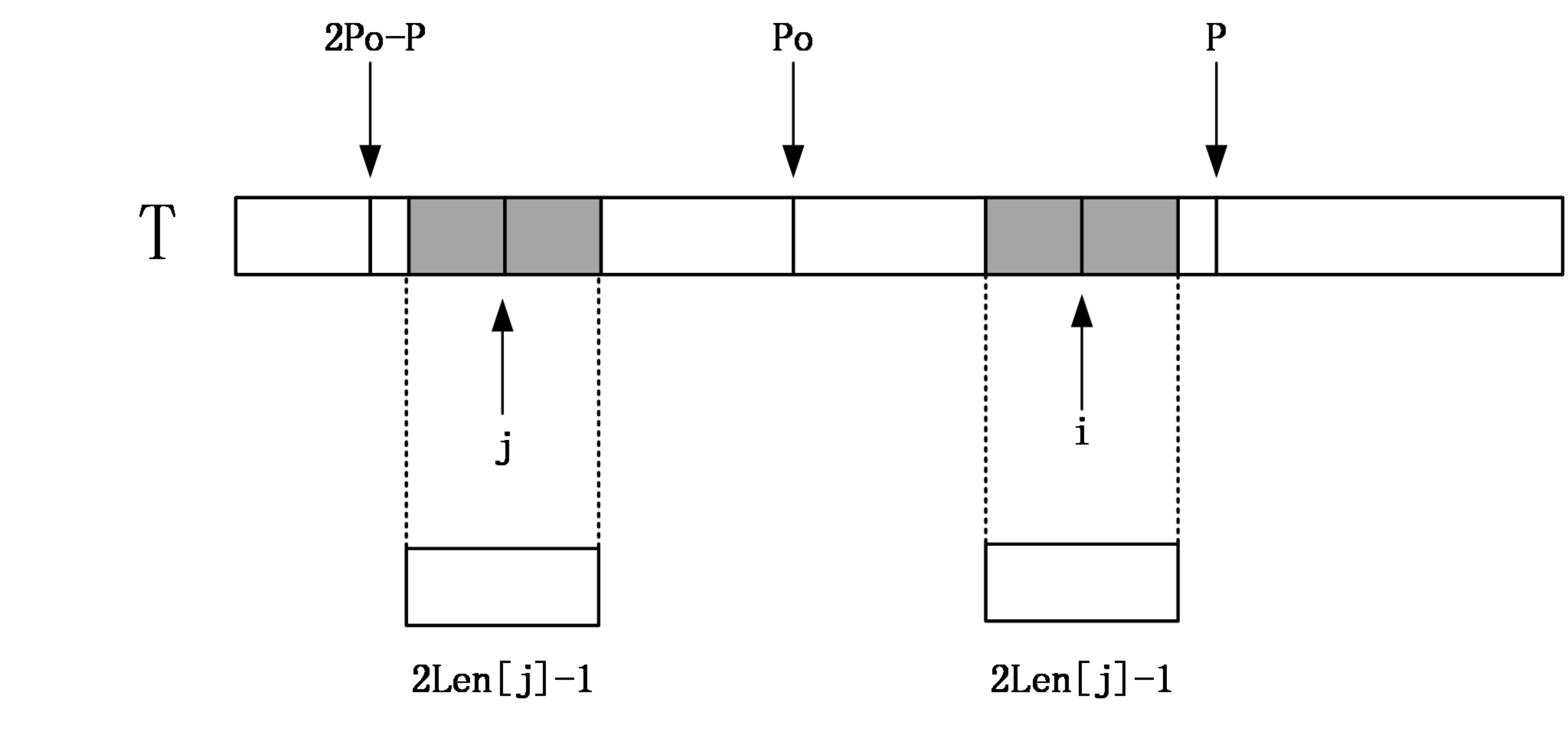
那麼找到i相對於po的對稱位置，設為j，那麼如果Len[j]<P-i，如下圖：

那麼說明以j為中心的迴文串一定在以po為中心的迴文串的內部，且j和i關於位置po對稱，由迴文串的定義可知，一個迴文串反過來還是一個迴文串，所以以i為中心的迴文串的長度至少和以j為中心的迴文串一樣，即Len[i]>=Len[j]。因為Len[j]<P-i,所以說i+Len[j]<P。由對稱性可知Len[i]=Len[j]。

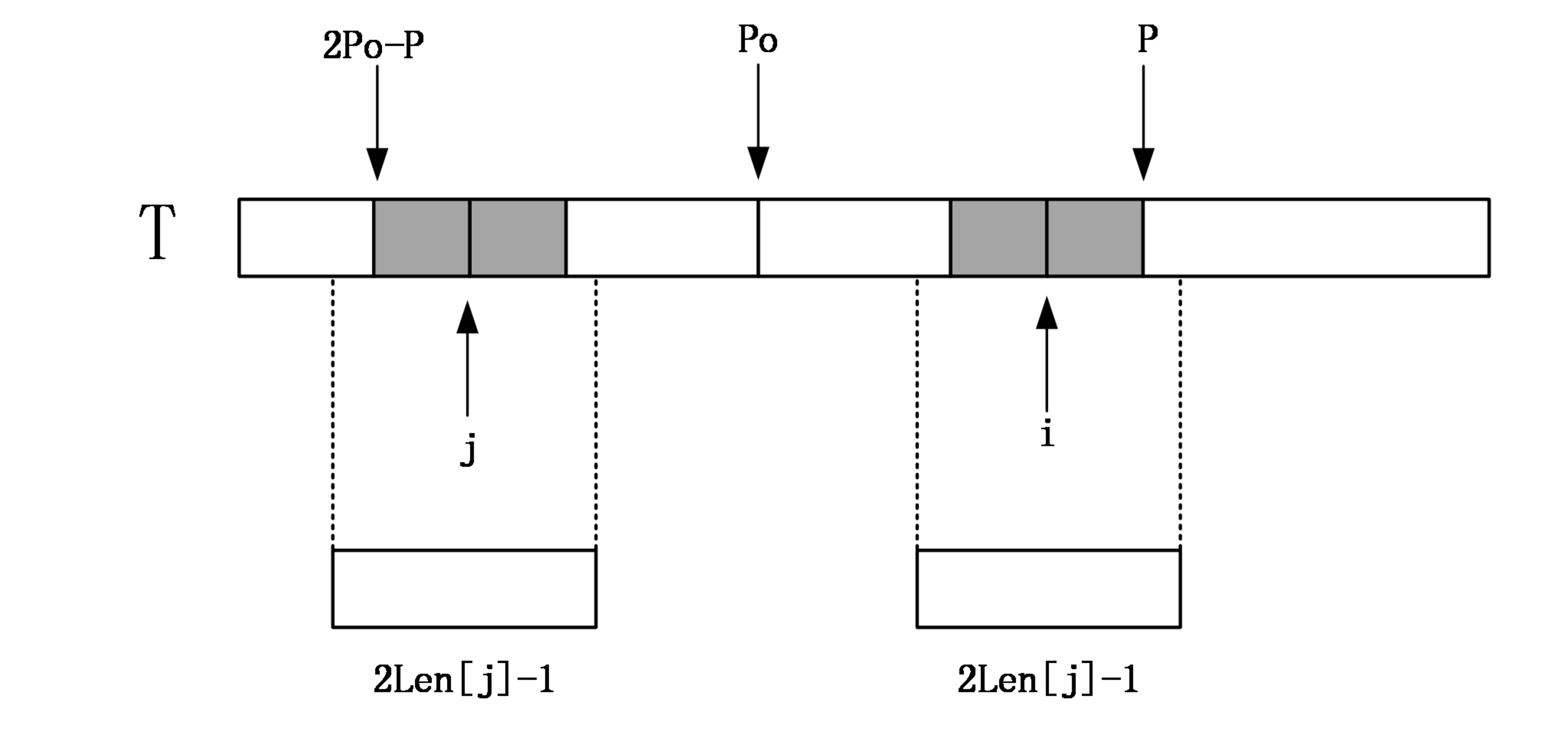
如果Len[j]>=P-i,由對稱性，說明以i為中心的迴文串可能會延伸到P之外，而大於P的部分我們還沒有進行匹配，所以要從P+1位置開始一個一個進行匹配，直到發生失配，從而更新P和對應的po以及Len[i]。

第二種情況: i>P

如果i比P還要大，說明對於中點為i的迴文串還一點都沒有匹配，這個時候，就只能老老實實地一個一個匹配了，匹配完成後要更新P的位置和對應的po以及Len[i]。

2.時間複雜度分析

Manacher演算法的時間複雜度分析和Z演算法類似，因為演算法只有遇到還沒有匹配的位置時才進行匹配，已經匹配過的位置不再進行匹配，所以對於T字串中的每一個位置，只進行一次匹配，所以Manacher演算法的總體時間複雜度為O(n)，其中n為T字串的長度，由於T的長度事實上是S的兩倍，所以時間複雜度依然是線性的。

下面是演算法的實現，注意，為了避免更新P的時候導致越界，我們在字串T的前增加一個特殊字元，比如說‘$’,所以演算法中字串是從1開始的。

const int maxn=1000010;  
char str[maxn];//原字串  
char tmp[maxn<<1];//轉換後的字串  
int Len[maxn<<1];  
//轉換原始串  
int INIT(char *st)  
{  
    int i,len=strlen(st);  
    tmp[0]='@';//字串開頭增加一個特殊字元，防止越界  
    for(i=1;i<=2*len;i+=2)  
    {  
        tmp[i]='#';  
        tmp[i+1]=st[i/2];  
    }  
    tmp[2*len+1]='#';  
    tmp[2*len+2]='$';//字串結尾加一個字元，防止越界  
    tmp[2*len+3]=0;  
    return 2*len+1;//返回轉換字串的長度  
}  
//Manacher演算法計算過程  
int MANACHER(char *st,int len)  (st即tmp，len即INIT的返回值）
{  
     int mx=0,ans=0,po=0;//mx即為當前計算迴文串最右邊字元的最大值  
     for(int i=1;i<=len;i++)  
     {  
         if(mx>i)  
         Len[i]=min(mx-i,Len[2*po-i]);//在Len[j]和mx-i中取個小  
         else  
         Len[i]=1;//如果i>=mx，要從頭開始匹配  
         while(st[i-Len[i]]==st[i+Len[i]])  
         Len[i]++;  
         if(Len[i]+i>mx)//若新計算的迴文串右端點位置大於mx，要更新po和mx的值  
         {  
             mx=Len[i]+i;  
             po=i;  
         }  
         ans=max(ans,Len[i]);  
     }  
     return ans-1;//返回Len[i]中的最大值-1即為原串的最長迴文子串額長度   
  }