可以分析，當n=1時，只有1個根節點，則只能組成1種形態的二叉樹，令n個節點可組成的二叉樹數量表示為h(n)，則h(1)=1; h(0)=1. 

      當n=2時，1個根節點固定，還有2-1個節點。這一個節點可以分成（1,0），（0,1）兩組。即左邊放1個，右邊放0個；或者左邊放0個，右邊放1個。即：h(2)=h(0)*h(1)+h(1)*h(0)=2，則能組成2種形態的二叉樹。

      當n=3時，1個根節點固定，還有2個節點。這2個節點可以分成（2,0），（1,1），（0,2）3組。即h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=5，則能組成5種形態的二叉樹。

以此類推，當n>=2時，可組成的二叉樹數量為h(n)=h(0)*h(n-1)+h(1)*h(n-2)+...+h(n-1)*h(0)種，即符合Catalan數的定義，可直接利用通項公式得出結果。

1、括號匹配問題

n對括號有多少種匹配方式？

n對括號相當於有2n個符號，n個左括號、n個右括號，可以設問題的解為f(2n)。第0個符號肯定為左括號，與之匹配的右括號必須為第2i+1字元。因為如果是第2i個字元，那麼第0個字元與第2i個字元間包含奇數個字元，而奇數個字元是無法構成匹配的。

    通過簡單分析，f(2n)可以轉化如下的遞推式 f(2n) = f(0)*f(2n-2) + f(2)*f(2n - 4) + ... + f(2n - 4)*f(2) + f(2n-2)*f(0)。簡單解釋一下，f(0) * f(2n-2)表示第0個字元與第1個字元匹配，同時剩餘字元分成兩個部分，一部分為0個字元，另一部分為2n-2個字元，然後對這兩部分求解。f(2)*f(2n-4)表示第0個字元與第3個字元匹配，同時剩餘字元分成兩個部分，一部分為2個字元，另一部分為2n-4個字元。依次類推。

    假設f(0) = 1，計算一下開始幾項，f(2) = 1, f(4) = 2, f(6) = 5。結合遞迴式，不難發現f(2n) 等於h(n)。

    

2、進棧出棧問題

一個棧(無窮大)的進棧序列為1，2，3，…，n，有多少個不同的出棧序列?

    這個與加括號的很相似，進棧操作相當於是左括號，而出棧操作相當於右括號。n個數的進棧次序和出棧次序構成了一個含2n個數字的序列。第0個數字肯定是進棧的數，這個數相應的出棧的數一定是第2i+1個數。因為如果是2i，那麼中間包含了奇數個數，這奇數個肯定無法構成進棧出棧序列。

    設問題的解為f(2n)， 那麼f(2n) = f(0)*f(2n-2) + f(2)*f(2n-4) + f(2n-2)*f(0)。f(0) * f(2n-2)表示第0個數字進棧後立即出棧，此時這個數字的進棧與出棧間包含的數字個數為0，剩餘為2n-2個數。f(2)*f(2n-4)表示第0個數字進棧與出棧間包含了2個數字，相當於1 2 2 1，剩餘為2n-4個數字。依次類推。

    假設f(0) = 1，計算一下開始幾項，f(2) = 1, f(4) = 2, f(6) = 5。結合遞迴式，不難發現f(2n) 等於h(n)。

3、二叉樹的種類問題

n個節點構成的二叉樹，共有多少種情形？

    可以這樣考慮，根肯定會佔用一個結點，那麼剩餘的n-1個結點可以有如下的分配方式，T(0, n-1),T(1, n-2),...T(n-1, 0)，設T(i, j)表示根的左子樹含i個結點，右子樹含j個結點。

    設問題的解為f(n)，那麼f(n) = f(0)*f(n-1) + f(1)*f(n-2) + .......+ f(n-2)*f(1) + f(n-1)*f(0)。假設f(0) = 1，那麼f(1) = 1, f(2) = 2, f(3) = 5。結合遞推式，不難發現f(n)等於h(n)。

4、網格路徑問題

對於一個n*n的正方形網格，每次我們能向右或者向上移動一格，那麼從左下角到右上角的所有在副對角線右下方的路徑總數為多少？

我們將一條水平邊記為進棧,垂直邊記為出棧，我們所要保證的就是前k步中水平邊的個數不小於垂直邊的個數，換句話說出棧的時候棧內一直有元素，所以從根本上說又迴歸到Catalan數了。

5、凸多邊形分割問題

求一個凸多邊形區域劃分成三角形區域的方法數？

    以凸多邊形的一邊為基，設這條邊的2個頂點為A和B。從剩餘頂點中選1個，可以將凸多邊形分成三個部分，中間是一個三角形，左右兩邊分別是兩個凸多邊形，然後求解左右兩個凸多邊形。

      設問題的解f(n)，其中n表示頂點數，那麼f(n) = f(2)*f(n-1) + f(3)*f(n-2) + ......f(n-2)*f(3) + f(n-1)*f(2)。f(2)*f(n-1)表示三個相鄰的頂點構成一個三角形，那麼另外兩個部分的頂點數分別為2和n-1。

      設f(2) = 1，那麼f(3) = 1, f(4) = 2, f(5) = 5。結合遞推式，不難發現f(n) 等於h(n-2)。

6、集合劃分問題

對於集合{1,2,3...2n}的不交叉劃分的數目為多少？

    這裡解釋一下不交叉劃分，我們對於集合{a,b}和{c,d}，假設他們組成了兩個區間[a,b]和[c,d]，我們假設兩個區間不重合，那麼以下四種情況當做是不交叉的：a<c<d<b，a<b<c<d，c<a<b<d與c<d<a<b，就是說兩個區間可以包含或者相離，那麼此時我們稱集合{a,b}和{c,d}是不交叉的。

    對於集合{1,2,3...2n}，將裡面元素兩兩分為一子集，共n個，若任意兩個子集都是不交叉的，那麼我們稱此時的這個劃分為一個不交叉劃分。此時不交叉的劃分數就是我們的了，證明也很容易，我們將每個子集中較小的數用左括號代替，較大的用右括號代替，那麼帶入原來的1至2n的序列中就形成了合法括號問題，就是我們之前得到過的結論。例如我們的集合{1,2,3,4,5,6}的不交叉劃分有五個：{{1,2},{3,4},{5,6}}，{{1,2},{3,6},{4,5}}，{{1,4},{2,3},{5,6}}，{{1,6},{2,3},{4,5}}和{{1,6},{2,5},{3,4}}。

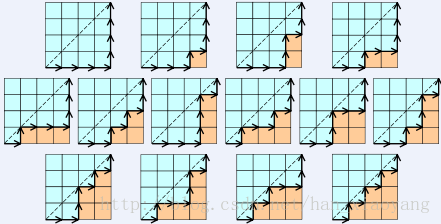
7、階梯切分問題

求n層的階梯切割為n個矩形的切法數

這個證明是怎麼進行的呢？我們先繪製如下的一張圖片，即n為5的時候的階梯：

我們注意到每個切割出來的矩形都必需包括一塊標示為*的小正方形，那麼我們此時列舉每個*與#標示的兩角作為矩形，剩下的兩個小階梯就是我們的兩個更小的子問題了，於是我們的C5 = C0 * C4 + C1 * C3 + C2 * C2 + C1 * C3 + C0 * C4，注意到這裡的式子就是我們前面的性質3,因此這就是我們所求的結果了。

8、乘積重組問題

矩陣鏈乘： P=a1×a2×a3×……×an，依據乘法結合律，不改變其順序，只用括號表示成對的乘積，試問有幾種括號化的方案？

    我們這樣考慮，首先通過括號化，將P分成兩個部分，然後分別對兩個部分進行括號化。比如分成(a1)×(a2×a3.....×an)，然後再對(a1)和(a2×a3.....×an)分別括號化；又如分成(a1×a2)×(a3.....×an)，然後再對(a1×a2)和(a3.....×an)括號化。

    設n個矩陣的括號化方案的種數為f(n)，那麼問題的解為

    f(n) = f(1)*f(n-1) + f(2)*f(n-2) + f(3)*f(n-3) + f(n-1)*f(1)。f(1)*f(n-1)表示分成(a1)×(a2×a3.....×an)兩部分，然後分別括號化。

    計算開始幾項，f(1) = 1, f(2) = 1, f(3) = 2, f(4) = 5。結合遞迴式，不難發現f(n)等於h(n-1)。

      

9、連線不想交問題

在圓上有2n個點，將這些點成對連線起來使得所得到的n條線段不相交的方法數？

    我們這樣考慮，以其中一個點為基點，編號為0，然後按順時針方向將其他點依次編號。那麼與編號為0相連點的編號一定是奇數，否則，這兩個編號間含有奇數個點，勢必會有個點被孤立，即在一條線段的兩側分別有一個孤立點，從而導致兩線段相交。設選中的基點為A，與它連線的點為B，那麼A和B將所有點分成兩個部分，一部分位於A、B的左邊，另一部分位於A、B的右邊。然後分別對這兩部分求解即可。

   設問題的解f(n)，那麼f(n) = f(0)*f(n-2) + f(2)*f(n-4) + f(4)*f(n-6) + ......f(n-4)*f(2) + f(n-2)*f(0)。f(0)*f(n-2)表示編號0的點與編號1的點相連，此時位於它們右邊的點的個數為0，而位於它們左邊的點為2n-2。依次類推。

   f(0) = 1, f(2) = 1, f(4) = 2。結合遞迴式，不難發現f(2n) 等於h(n)。

10、高矮排隊問題

2n個高矮不同的人,排成兩排,每排必須是從矮到高排列,而且第二排比對應的第一排的人高,問排列方式有多少種?

先將2n個人從低到高排列，然後，用0表示對應的人在第一排,用1表示對應的人在第二排,那麼含有n個0,n個1的序列,就對應一種方案. 
比如00...011...1就對應著 
第一排:1     2     3    ...n
第二排:n+1  n+2  n+3  ...2n 

而010101...01對應著

第一排:1   3   5  ...2n-1
第二排:2   4   6  ...2n 

    問題轉換為,這樣的滿足條件的01序列有多少個. 
    觀察1的出現,我們考慮它能不能放在第二排,顯然,在這個1之前出現的那些0和1對應的人 要麼是在這個1左邊,要麼是在這個1前面。而即使前面0和1剛好配對，也一定要留出一個0在這個1前面，也就是要求之前的0的個數大於1的個數. 
    如果把0看成入棧操作,1看成出棧操作,就是說給定2n個元素,合法的入棧出棧序列有多少個。這就是catalan數,其通項是c(2n, n)/(n+1). 

11、格子填數問題

在一個2*n的格子中填入1到2n這些數值使得每個格子內的數值都比其右邊和上邊的所有數值都小的情況數

    這一題和上一題排隊是一樣的思路。

12、門票找錢問題   

有2n個人排成一行進入劇場。入場費5元。其中只有n個人有一張5元鈔票，另外n人只有10元鈔票，劇院無其它鈔票，問有多少中方法使得只要有10元的人買票，售票處就有5元的鈔票找零？

可以將持5元買票視為進棧，那麼持10元買票視為5元的出棧。這個問題就轉化成了棧的出棧次序數。由應用三的分析直接得到結果，f(2n) 等於h(n)。

四、Catalan數的一個變形應用

上面第12小題的一個延伸：n+m個人排隊買票，並且滿足n>= m，票價為5元，其中n個人各手持一張5元鈔票，m個人各手持一張10元鈔票，除此之外大家身上沒有任何其他的錢幣，並且初始時候售票視窗沒有錢，問有多少種排隊的情況數能夠讓大家都買到票。

    這個題目是Catalan數的變形，不考慮人與人的差異，如果m=n的話那麼就是我們初始的Catalan數問題，也就是將手持5元的人看成是入棧，手持10元的人看成是出棧，出棧序列的個數。

    這個題目區別就在於n>m的情況，此時我們仍然可以用原先的證明方法考慮，假設我們要的情況數是D(n+m)，無法讓每個人都買到的情況數是U(n + m)，那麼就有D(n+m) + U(n +m) = C(m+n, n)，此時我們求U(n + m)，我們假設最早買不到票的人編號是k，他手持的是10元並且售票處沒有錢，那麼將前k個人的錢從5元變成10元，從10元變成5元，這時候就有n+1個人手持5元，m-1個手持10元的，所以就得到U(n + m) = C(n + m, n + 1)，於是我們的結果就因此得到了，表示式是D(n + m) = C(n + m, n) - C(n + m, n + 1)。