2012年第三屆藍橋杯C/C++程式設計本科B組省賽 放棋子(程式碼填空)

放棋子    
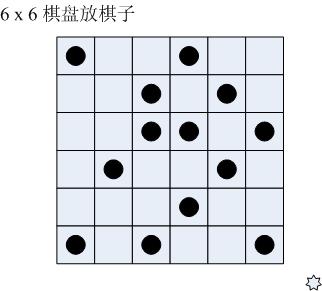
今有 6 x 6 的棋盤格。其中某些格子已經預先放好了棋子。現在要再放上去一些，使得：每行每列都正好有3顆棋子。我們希望推算出所有可能的放法。下面的程式碼就實現了這個功能。

初始陣列中，“1”表示放有棋子，“0”表示空白。

int N = 0;  
  
bool CheckStoneNum(int x[][6])  
{  
    for(int k=0; k<6; k++)  
    {  
        int NumRow = 0;  
        int NumCol = 0;  
        for(int i=0; i<6; i++)  
        {  
            if(x[k][i]) NumRow++;  
            if(x[i][k]) NumCol++;  
        }  
        if(_____________________) return false;  // 填空  
    }  
    return true;  
}  
  
int GetRowStoneNum(int x[][6], int r)  
{  
    int sum = 0;  
    for(int i=0; i<6; i++)   if(x[r][i]) sum++;  
    return sum;  
}  
  
int GetColStoneNum(int x[][6], int c)  
{  
    int sum = 0;  
    for(int i=0; i<6; i++)   if(x[i][c]) sum++;  
    return sum;  
}  
  
void show(int x[][6])  
{  
    for(int i=0; i<6; i++)  
    {  
        for(int j=0; j<6; j++) printf("%2d", x[i][j]);  
        printf("\n");  
    }  
    printf("\n");  
}  
  
void f(int x[][6], int r, int c);  
  
void GoNext(int x[][6],  int r,  int c)  
{  
    if(c<6)  
        _______________________;   // 填空  
    else  
        f(x, r+1, 0);  
}  
  
void f(int x[][6], int r, int c)  
{  
    if(r==6)  
    {  
        if(CheckStoneNum(x))  
        {  
            N++;  
            show(x);  
        }  
        return;  
    }  
  
    if(______________)  // 已經放有了棋子  
    {  
        GoNext(x,r,c);  
        return;  
    }  
      
    int rr = GetRowStoneNum(x,r);  
    int cc = GetColStoneNum(x,c);  
  
    if(cc>=3)  // 本列已滿  
        GoNext(x,r,c);    
    else if(rr>=3)  // 本行已滿  
        f(x, r+1, 0);     
    else  
    {  
        x[r][c] = 1;  
        GoNex。t(x,r,c);  
        x[r][c] = 0;  
          
        if(!(3-rr >= 6-c || 3-cc >= 6-r))  // 本行或本列嚴重缺子，則本格不能空著！  
            GoNext(x,r,c);    
    }  
}  
  
int main(int argc, char* argv[])  
{  
    int x[6][6] = {  
        {1,0,0,0,0,0},  
        {0,0,1,0,1,0},  
        {0,0,1,1,0,1},  
        {0,1,0,0,1,0},  
        {0,0,0,1,0,0},  
        {1,0,1,0,0,1}  
    };  
  
    f(x, 0, 0);  
      
    printf("%d\n", N);  
  
    return 0;  
}

答案：NumRow != 3 || NumCol != 3
           f(x, r, c + 1)
           x[r][c] == 1