2012年第三屆藍橋杯C/C++程式設計本科B組省賽 大數乘法(程式碼填空)

大數乘法
對於32位字長的機器，大約超過20億，用int型別就無法表示了，我們可以選擇int64型別，但無論怎樣擴充套件，固定的整數型別總是有表達的極限！如果對超級大整數進行精確運算呢？一個簡單的辦法是：僅僅使用現有型別，但是把大整數的運算化解為若干小整數的運算，即所謂：“分塊法”。
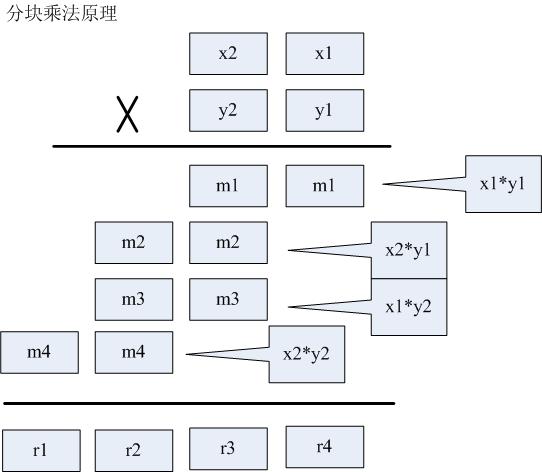
如圖【1.jpg】表示了分塊乘法的原理。可以把大數分成多段（此處為2段）小數，然後用小數的多次運算組合表示一個大數。可以根據int的承載能力規定小塊的大小，比如要把int分成2段，則小塊可取10000為上限值。注意，小塊在進行縱向累加後，需要進行進位校正。

以下程式碼示意了分塊乘法的原理（乘數、被乘數都分為2段）。

void bigmul(int x, int y, int r[])  
{  
    int base = 10000;  
    int x2 = x / base;  
    int x1 = x % base;   
    int y2 = y / base;  
    int y1 = y % base;   
  
    int n1 = x1 * y1;   
    int n2 = x1 * y2;  
    int n3 = x2 * y1;  
    int n4 = x2 * y2;  
  
    r[3] = n1 % base;  
    r[2] = n1 / base + n2 % base + n3 % base;  
    r[1] = ____________________________________________; // 填空  
    r[0] = n4 / base;  
      
    r[1] += _______________________;  // 填空  
    r[2] = r[2] % base;  
    r[0] += r[1] / base;  
    r[1] = r[1] % base;  
}  
  
  
int main(int argc, char* argv[])  
{  
    int x[] = {0,0,0,0};  
  
    bigmul(87654321, 12345678, x);  
  
    printf("%d%d%d%d\n", x[0],x[1],x[2],x[3]);  
  
    return 0;  
}  

答案： n2 / base + n3 / base + n4 % base
            r[2] / base