從面試題中學演算法(2)---求陣列中唯一n個出現1次的數字(n=1,2,3)

       題目要求：給定一個整數陣列，其中只有1個數出現1次，其他數字都出現偶數次。找出這個數字。如果其中只有2個數字出現1次呢？3個數字出現一次呢？依次找出。

   例子：陣列a[] ={1,2,3,4,2,1,3} 那麼程式輸出 僅出現一次的數字為4。陣列a[] = {1,2,3,2,3,4}.那麼程式輸出2個僅出現一次的數字為1,4. 陣列a[]= {1,2,3,3,2,4,6}那麼程式輸出 3個僅出現一次的數為1,4,6.

好了，題目理解清楚了，下面就考慮解法了。首先，說明一個位運算---異或。這個對解題非常重要。異或是位運算的一種，指的是兩個數字的二進位制，每個位逐一異或。兩個位相同則該位為0，不同則為1。異嘛，肯定不同為1.比如：3 ^ 4 = (011)^(100) =(111)。並且異或滿足交換律。這個交換律很重要。x=a^b^c=a^c^b。0和x異或都為x。

下面說明3個非常重要的等式。

1. -n = (~n+1) = ~(n-1)   

        一個數取負數運算將等於該數按位取反加1，並且也等於該值減1取反。從補碼角度理解，第二個式子恰好為負數的補碼（負數的補碼為原始碼取反加1）對應於n而言，其負數就為-n嘛。

2.保留一個數字的最右邊為1的位，其他位都置為0.   n = n &(~n+1 )

比如n為十進位制 7，對應二進位制為0111.那麼保留該數字的最右邊1為： n = n &(~n+1 )=0001。可見只保留了最右邊位為1的位。

3.將一個數的最右邊1變為0，其餘的位不變。 n = n &(n-1) .比如n為 十進位制7，對應二進位制為0111.n = n &(n-1) =0110。僅將最右邊為1的位變為0。

一.找出1個僅出現一次的數字

在陣列中，只有一個數字出現一次，其他數字都成對出現，那麼如果對整個陣列進行異或操作呢？由於異或操作滿足交換律，而兩個相同的數字之間異或為0，而0和任意數異或都為任意數。所以遍歷一遍陣列，且依次將結果異或，最後的異或值就是所查詢的數字。比如a[] ={1,2,3,4,2,1,3}  xorRst 為異或值。將陣列中所有元素異或下。xorRst =1^2^3^4^2^1^3。根據交換律xorRst =(1^1)^(2^2)^(3^3)^4其中括號內的值都為0.所以xorRst =0^0^0^4=4.即是結果。程式碼如下：

int FindSingleNum(int a[],int len)
{	
	int Rst = 0;
	if(a != NULL && len > 0)
	{
		for(int i=0 ; i<len; ++i)
			Rst ^= a[i];
	}
	return Rst ;
}

二.找出2個僅出現一次的數字

       那麼問題升級為陣列中有2個僅出現一次的數字。既然我們有了上面的分析，那麼2個數字的能不能按照上面思路走呢？如果我們找到了區分這個2個數字的規則，就可以將該2個數字分到2組中去，而對於每個組而言，都可以按照出現1個數字的方法解決。那麼問題就解決了。那現在是如何區分這個兩個數字呢？我們還是將所有元素進行異或後結果。xorRst = a^b。（a,b為僅出現1次的2個數，其他成對的數都異或為0了，見前面分析）。由於a,b不同，所以a,b的對應的每個位至少有一個位不同，我們如果找出這個了位，那麼a,b就可以依次分入到兩個不同的組中去。而xorRst的最右邊為1的數（如何求就是前面介紹的3個等式之一）。就完全表示。假設xorRst最右邊為1的位是第m位。則a,b的第m位肯定不同。依次來將陣列元素進行分組，相同的數字肯定是會分入到同一組中（因為相同的數每位都相同）。

int LastBitof1(int num)
{
	return num & (~num+1) ;
}
bool FindTwoOnceNum(int a[],int len,int &first,int &second)
{	
	bool RstState = false ;
	if(a != NULL && len > 0)
	{	
		int xorRst = 0 ;
		for(int i= 0 ; i < len ; ++i)
			xorRst ^= a[i] ;
		xorRst = xorRst & (~xorRst +1 );//get last bit of 1
		first = second = 0 ;
		for(int j=0 ;j<len ;++j)
		{
			if(a[j] & xorRst ) //通過xorRst 來分組
				first ^= a[j];
			else
				second ^= a[j];
		}
		RstState = true ; 
	}
	return RstState ;
}

三.找出3個僅出現一次的數字

那麼問題如果在升級，一個陣列中有3個僅出現一次的數字呢？有了前面兩個問題的思路，我們猜想，也就是該如何進行分組？將a,b,c三個數如果分入到2個組中，分別對兩組求解異或值，其中一組的異或結果就是a,b,c中的一個，有了這個，那麼問題就回到第二個問題了。也就解決了。那麼關鍵是如何進行a,b,c的分組呢？如何找到一個卻別a,b,c的方法呢？

依然繼續將陣列中所有的元素進行異或求值。其結果為 xorRst = a^b^c（a,b,c為三個僅出現一次的數）。

下面將開啟一連串的邏輯推導。

1.由於a,b,c三個數互不相等。所以xorRst與a,b,c都不相等。

證明：假設xorRst與a相等。 則  a = a^b^c.那麼 b^c=0 ,即是 b等於c，與a,b,c互不相等矛盾。

2.因為xorRst與a,b,c都不相等。所以xorRst^a,xorRst^b,xorRst^c都不為0.（兩個不同數異或結果肯定不為0）

3.假設有這樣一個函式f(n)=lastBifof1(n)（問題2程式碼中的一個函式），f(n)函式目的就是保留數n的最右邊1位，其他位都置為0。這是前面提到的3個等式中的一個。所以看下：這樣的結果

f(xorRst ^a ) ^f(xorRst ^b ) ^f(xorRst ^c )  。這個式子意思就是，分別求xorRst^a,xorRst^b,xorRst^c最右邊為1的位。然後將結果異或起來。從二進位制角度看，其實也就是 三個只有一個位為1的數進行異或。因為f(xorRst ^a ) , f(xorRst ^b ) ,f(xorRst ^c ) 三個數都不為0.所以f(xorRst ^a ) ^ f(xorRst ^b ) ^f(xorRst ^c ) 結果也不為0(如果該結果為0，那麼至少有一個f(xorRst^n)(n=a,b,c)為0，與前面f(xorRst^a,b,c)不為0矛盾。

所以該條結論：A= f(xorRst ^a ) ^ f(xorRst ^b ) ^f(xorRst ^c ) 不為0. 即是至少有一位為1.

4. 假設A的第m位為1，那麼得出的結論就是 xorRst ^a,xorRst^b,xorRst^c 這三個數中僅有一個數的第m位為1或者三個數的第m位都為1.(這是很好得出的 1=1^1^1或者 1=0^1^0 就這兩種情況）。

下面證明：xorRst ^a,xorRst^b,xorRst^c 三個數的第m位都為1的情況是不可能的。

證明：假設xorRst^a,xorRst^b，xorRst^c 第m位都為1.那麼xorRst 的第m位都與a,b,c的第m位相反（位不同才為1嘛）。那麼也就是a,b,c的第m位都相同。

4.1 假設a,b,c的第m位都為0.因為xorRst與a,b,c在第m位都相反，所以 xorRst 的第m位為1.有因為xorRst=a^b^c。所以在xorRst在第m位上是為0的。與前面矛盾。

4.2 假設a,b,c的第m位都為1.因為xorRst與a,b,c在第m位都相反，所以 xorRst 的第m位為0，又因為xorRst=a^b^c 所以xorRst的第m位為1.與前面的矛盾。

5.結論：xorRst ^a,xorRst^b,xorRst^c 這三個數中僅有一個數的第m位為1。由此找到了區分a,b,c三者的方法。那麼依據xorRst ^n的第m位來分組a,b,c三個數進入到兩個不同組中去。

void Swap(int &a,int &b)
{
	int tmp = a;
	a = b;
	b = tmp;
}
bool FindTreeOnceNum(int a[],int len, int &first,int &second, int &third)
{
	bool RstState = false ;
	if(a != NULL && len > 0)
	{
		
		int xorRst = 0,i;//異或結果
		for(i=0; i<len; ++i)
			xorRst ^= a[i];
		//下面求 f(x^a)^f(x^b)^f(x^c)的最右邊為1的第m位
		int  flag =0;
		for(i=0 ; i<len ; ++i)
			flag ^= LastBitof1(xorRst ^ a[i]);
		flag = LastBitof1(flag); //只保留最右邊為1的位
		//求first
		first = second = third = 0 ;
		vector<int> vec;
		for(i=0 ; i<len ;++i)
			if(LastBitof1( xorRst ^ a[i] ) == flag )//x^a的第m位為1的情況 這裡的m位其實是最右邊為1位
				first ^= a[i];  //這樣first 就求出了
		for(i=0 ; i<len ;++i)
			if( a[i] == first)
				Swap(a[i],a[len-1]);//移除該first值
		FindTwoOnceNum(a,len-1,second,third);
		RstState = true; 
	}
	return RstState ;
}

四.完整程式碼及其測試

#include <iostream>
#include <vector>
using namespace std;

int FindSingleNum(int a[],int len)
{	
	int Rst = 0;
	if(a != NULL && len > 0)
	{
		for(int i=0 ; i<len; ++i)
			Rst ^= a[i];
	}
	return Rst ;
}

int LastBitof1(int num)
{
	return num & (~num+1) ;
}
bool FindTwoOnceNum(int a[],int len,int &first,int &second)
{	
	bool RstState = false ;
	if(a != NULL && len > 0)
	{	
		int xorRst = 0 ;
		for(int i= 0 ; i < len ; ++i)
			xorRst ^= a[i] ;
		xorRst = xorRst & (~xorRst +1 );//get last bit of 1
		first = second = 0 ;
		for(int j=0 ;j<len ;++j)
		{
			if(a[j] & xorRst ) //通過xorRst 來分組
				first ^= a[j];
			else
				second ^= a[j];
		}
		RstState = true ; 
	}
	return RstState ;
}
void Swap(int &a,int &b)
{
	int tmp = a;
	a = b;
	b = tmp;
}
bool FindTreeOnceNum(int a[],int len, int &first,int &second, int &third)
{
	bool RstState = false ;
	if(a != NULL && len > 0)
	{
		
		int xorRst = 0,i;//異或結果
		for(i=0; i<len; ++i)
			xorRst ^= a[i];
		//下面求 f(x^a)^f(x^b)^f(x^c)的最右邊為1的第m位
		int  flag =0;
		for(i=0 ; i<len ; ++i)
			flag ^= LastBitof1(xorRst ^ a[i]);
		flag = LastBitof1(flag); //只保留最右邊為1的位
		//求first
		first = second = third = 0 ;
		vector<int> vec;
		for(i=0 ; i<len ;++i)
			if(LastBitof1( xorRst ^ a[i] ) == flag )//x^a的第m位為1的情況 這裡的m位其實是最右邊為1位
				first ^= a[i];  //這樣first 就求出了
		for(i=0 ; i<len ;++i)
			if( a[i] == first)
				Swap(a[i],a[len-1]);//移除該first值
		FindTwoOnceNum(a,len-1,second,third);
		RstState = true; 
	}
	return RstState ;
}
void printArray(int a[],int len)
{
	if( a != NULL && len > 0)
	{
		for(int i=0 ; i<len; ++i)
			cout<<a[i]<<" ";
		cout<<"\n";
	}
}
void Test1()
{	
	int a[] = {1,2,3,4,3,2,1};
	int len = sizeof(a)/sizeof(int);
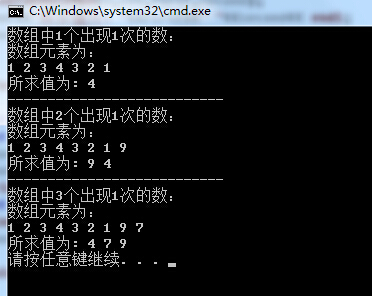
	cout<<"陣列中1個出現1次的數：\n";
	cout<<"陣列元素為：\n";
	printArray(a,len);
	cout<<"所求值為: "<<FindSingleNum(a,len)<<endl;
	cout<<"---------------------------\n";
}
void Test2()
{	
	int a[] = {1,2,3,4,3,2,1,9};
	int len = sizeof(a)/sizeof(int);
	cout<<"陣列中2個出現1次的數：\n";
	cout<<"陣列元素為：\n";
	printArray(a,len);
	int first ,second;
	FindTwoOnceNum(a,len,first,second);
	cout<<"所求值為: "<<first<<" "<<second<< endl;
	cout<<"---------------------------\n";
	
}
void Test3()
{	
	int a[] = {1,2,3,4,3,2,1,9,7};
	int len = sizeof(a)/sizeof(int);
	cout<<"陣列中3個出現1次的數：\n";
	cout<<"陣列元素為：\n";
	printArray(a,len);
	int first ,second,third;
	FindTreeOnceNum(a,len,first,second,third);
	cout<<"所求值為: "<<first<<" "<<second<<" " <<third<< endl;
}
int main()
{
	Test1();
	Test2();
	Test3();
	return 0 ;
}

六.參考資料

http://zhedahht.blog.163.com/blog/static/25411174201283084246412/何海濤的部落格 劍指offer作者