實戰資料結構(12)_二叉樹的線索化

     二叉樹的線索化，花了點時間去整理。整個遞迴過程還是有些抽象的。為什麼要進行二叉樹的線索化，目的就是為了節省使用二叉連結串列實現過程中，太多的NULL指標。如果把這些空指標都利用起來，串起來一個迴圈雙向連結串列，那麼對於查詢是非常方便的。對於查詢而言，如中序遍歷，我們關心的是一個節點的後繼節點和前驅節點。
因為對於未線索化的二叉樹而言，只能從某個節點來獲取它的左右孩子節點，也就說只能置頂向下，而不能同過節點快速找到其前驅節點，如果要獲取的話，又要遍歷一次。
     所以，線索化，就能清楚的知道某個節點的前驅和後繼節點，這樣將那些空餘的節點利用起來了，而且查詢也方便了。
下面就是程式碼的實現：
(1) 線索二叉樹的資料結構
(2) 建立二叉樹，並且線索化
(3)線索化的二叉樹的遍歷，注意不能使用遞迴了。
(4)線索化的二叉樹的查詢。

/***********************************************************************
二叉樹的線索化
(1)建立二叉樹（按照帶括號的字串)
(2)二叉樹的線索化
(3)二叉樹線索化後遍歷
(4)查詢某個值的 先驅節點
(5)查詢某個值的 後繼節點
************************************************************************/
#include <cstdio>

typedef enum {Link,Thread} PointFlag; //定義列舉量 pointflag為二者之一
typedef struct Node
{
	char ch;							// 資料域
	struct Node *plchild,*prchild;		// 左右節點指標
	PointFlag lflag,rflag;				// 標誌位 link為 連線 thread為線索標誌
}BiTreeNode;
const int MAX=20;
//按照字串建立 A(B(,D(G)),C(E(,H),F))  16:30
void CreateBiTree_ByString(BiTreeNode * &T,char str[])
{
	BiTreeNode *p=NULL;
	int flag=0,top=0;//flag=1左孩子，flag=2右孩子 top為棧量
	BiTreeNode *Stack[MAX];	//棧 用於存父節點
	while(*str)
	{
		switch(*str)
		{
			case '(': //則剛建立的節點為 父節點入棧
				Stack[top++]=p;
				flag=1;
				break;
			case ',':
				flag=2;
				break;
			case ')':
				top--;	//構造完畢了棧頂節點的左右孩子 出棧
				break;
			default:
				p=new BiTreeNode ;
				if(NULL==p)	return ;
				p->ch=*str;
				p->plchild=p->prchild=NULL;
				p->lflag=p->rflag=Link;
				if(T==NULL)		//建立根節點
					T=p;
				else
				{	
					switch(flag)
					{
						case 1:
							Stack[top-1]->plchild=p; //p為左孩子
							break;
						case 2:
							Stack[top-1]->prchild=p; //p為右孩子
							break;
					}
				/*	if(Stack[top-1]->plchild)
						Stack[top-1]->lflag=Link;
					if(Stack[top-1]->prchild)
						Stack[top-1]->rflag=Link;*/
				}
				break;
		}
		++str;
	}
}
void LDR_Traverse(BiTreeNode *T)
{
	if(T)
	{	
		LDR_Traverse(T->plchild);
		printf("%2c",T->ch);
		LDR_Traverse(T->prchild);
	}
}

BiTreeNode *g_pre;	//全域性

/***********************************************************************
二叉樹進行中序遍歷線索化
難點：寫法上和中序遍歷一樣。先不斷的訪問左子樹的最左節點（中序的思路）
	  那麼如何進行前驅和後繼節點的連線呢？ 
前驅: 是完成當前指標p的前驅
後繼：是完成之前節點的後繼
***********************************************************************/
void LDR_Traverse_Thread(BiTreeNode *p)
{
	if(p)
	{
		LDR_Traverse_Thread(p->plchild); //將左子樹線索化
		if(p->plchild==NULL)	//一直遍歷到最左子節點 葉子節點或者只有右子樹
		{	//p更新 前驅節點
			p->lflag=Thread;	//p的左孩子節點 標誌為 前驅
			p->plchild=g_pre;	// g_pre儲存為上一個訪問的節點(按照中序遍歷順序)
		}
		if(g_pre->prchild==NULL) //
		{	
			g_pre->rflag=Thread;
			g_pre->prchild=p;
		}
		g_pre=p;	//p已經遍歷過 pre指向剛遍歷過的節點
		LDR_Traverse_Thread(p->prchild);
	}
}
//二叉樹的線索化
BiTreeNode* BiTreeThread(BiTreeNode*  &T)
{	
	//構造頭結點
	BiTreeNode *p=new BiTreeNode;
	if(!p || !T)	return NULL;
	
	//頭節點處理
	p->lflag=Link;
	p->rflag=Thread;
	p->plchild=T;	//頭結點左孩子 指向根節點
	p->prchild=p;	//頭結點右孩子 指向自己
	
	g_pre=p;		//g_pre初始化 指向頭節點
	LDR_Traverse_Thread(T);	//將T樹進行線索化
	
	//最後一個節點處理
	g_pre->rflag=Thread;	//最後一個節點 標誌位
	g_pre->prchild=p;		//最後一個節點 後繼指向頭節點
	p->prchild=g_pre;		//頭節點後繼為 最後一個節點
	
	return p;	//返回頭節點
}

//中序非遞迴 遍歷線索化 後
void LDR_Travese_AfterThread(BiTreeNode *T)
{
	BiTreeNode *p=T->plchild; //p為根節點
	while(p!=T)
	{
		while(p->lflag==Link)
			p=p->plchild;
		printf("%2d %2c %2d \n",p->lflag,p->ch,p->rflag);
		while(p->rflag==Thread && p->prchild !=T) //如果 p有後繼節點則 直接通過後繼節點訪問下一個 節點
		{
			p=p->prchild;
			printf("%2d %2c %2d \n",p->lflag,p->ch,p->rflag);
		}
		p=p->prchild;
	}
}
//找到指定節點的前驅節點
BiTreeNode *FindPointNode(BiTreeNode *Head,char key)
{
	BiTreeNode *p=Head->plchild; //獲取根節點
	while(p!=Head)
	{
		while(p->lflag==Link)
			p=p->plchild;
		if(p->ch== key)
			return p;
		while(p->rflag == Thread && p->prchild !=Head )
		{
			p=p->prchild;
			if(p->ch == key)
				return p;
		}
		p=p->prchild;
	}
	return NULL;
}	
//找到指定節點的後繼節點
//就是根據 rflag==1直接找到，後者去找該節點右子樹最左節點
BiTreeNode *FindNextNode(BiTreeNode *p)
{	
	BiTreeNode *pre=NULL;
	if(p->rflag==Thread)
		return p->prchild;
	else {
		pre=p->prchild;
		while(pre->lflag==Link)
			pre=pre->plchild;
		return pre;
	}
}
//找指定節點的前驅節點
//如果該節點的lflag==1直接返回，否則就找到該節點的左子樹的最右節點
BiTreeNode *FindPreNode(BiTreeNode *p)
{
	BiTreeNode *pre=NULL;
	if(p->lflag==Thread)
		return p->plchild;
	else {
		pre=p->plchild;
		while(pre->rflag==Link)
			pre=pre->prchild;
		return pre;
	}
}
int main()
{	
	BiTreeNode *T=NULL;
	CreateBiTree_ByString(T,"A(B(,D(G)),C(E(,H),F))");
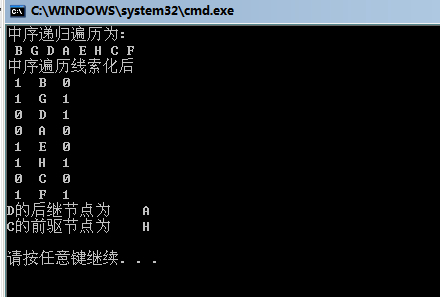
	puts("中序遞迴遍歷為:");
	LDR_Traverse(T);
	printf("\n");
	BiTreeNode *head=BiTreeThread(T);
	puts("中序遍歷線索化後");
	LDR_Travese_AfterThread(head);
	BiTreeNode *pos=FindPointNode(head,'D');
	printf("D的後繼節點為\t%2c\n",FindNextNode(pos)->ch);
	pos=FindPointNode(head,'C');
	printf("C的前驅節點為\t%2c\n",FindPreNode(pos)->ch);
	printf("\n");
	return 0;
}