五大經典查詢(1)_二叉排序樹查詢

/***********************************************************************
五大經典查詢(5)：利用二叉排序樹--查詢
(1) 二叉排序樹生成 
(2) 二叉樹的中序遍歷 LDR_BiTreeTraverse
(3) 二叉排序樹的插入
(4) 二叉排序樹的刪除
**********************************************************************/
#include <cstdio> 
typedef struct Tree_Node //定義二叉排序樹結構
{
	int data;
	struct Tree_Node *plchild;
	struct Tree_Node *prchild;
}BSTreeNode;	

// 插入二叉排序樹
// T為父節點 
void InsertBSTree(BSTreeNode *FatherNode,int key, bool &flag)
{
	if(FatherNode==NULL) //判斷當前父節點是否為空
		return ;
	if(key < FatherNode->data) //如果key < 父節點
		InsertBSTree(FatherNode->plchild,key,flag) ;// 插入到 左子樹中
	else 
		InsertBSTree(FatherNode->prchild,key,flag); // 插入到 右子樹中
	if(!flag)
	{ //構造新節點 用Key初始化 
		BSTreeNode *p=new BSTreeNode;
		if(NULL==p)	
			return ;
		p->data=key;
		p->plchild=NULL;
		p->prchild=NULL;
		//父節點連結新建節點
		if(key < FatherNode->data) //key<父節點 新建p為左孩子節點
			FatherNode->plchild=p;
		else
			FatherNode->prchild=p;
		flag=true;
	}
}
// 利用陣列--建立二叉排序樹
void CreateBSTree(BSTreeNode* &RootNode,int a[],int len)
{
	if(RootNode==NULL) //完成根節點的構造
	{
		RootNode=new BSTreeNode;
		if(RootNode==NULL)	
			return ;
		RootNode->data=a[0];
		RootNode->plchild=NULL;
		RootNode->prchild=NULL;
	}
	bool flag;
	for(int i=1;i<len;i++)
	{	
		flag=false;
		InsertBSTree(RootNode,a[i],flag);
	}
}
// 二叉樹的中序遍歷 遞迴處理
void LDR_BiTreeTraverse(BSTreeNode  *RootNode)
{
	if(RootNode)
	{
		LDR_BiTreeTraverse(RootNode->plchild);
		printf("%d ",RootNode->data);
		LDR_BiTreeTraverse(RootNode->prchild);
	}
}
//搜尋二叉排序樹
BSTreeNode* SearchBST(BSTreeNode* RootNode,int key)
{
	if(!RootNode) //到底了 
		return NULL;
	if(key == RootNode->data)
		return RootNode;
	else 
	{
		if(key < RootNode->data)
			return SearchBST(RootNode->plchild,key);
		else 
			return SearchBST(RootNode->prchild,key);
	}
}
//刪除 指定節點
void DeleteNode(BSTreeNode *p)
{
	BSTreeNode *q;
	// 刪除節點為 葉子節點或 只有左子樹 或 只有右子樹 直接連線即可
	if(p->plchild ==NULL)// 若刪除節點左子樹為空。
	{	
		q=p;
		p=p->prchild; //重新連結右子樹
		delete q;
	}
	else
	{ 
		if(p->prchild==NULL)// 若刪除節點右子樹為空。
		{
			q=p;
			p=p->plchild;//重新連結左子樹
			delete q;
		}
		else  // 左右子樹都不為空  查詢前驅指標
		{	
			q=p;
			BSTreeNode *cur=p->plchild; //cur指向 刪除節點的左子樹
			while(cur->prchild)	 // 查詢 刪除節點左子樹中 最右節點	 按照中序遍歷的前驅
			{
				q=cur;
				cur=cur->prchild;
			}
			p->data=cur->data;	//刪除 指定節點資料
			if(p!=q)
				q->prchild=cur->plchild; //重接 q的右子樹
			else // p==q  就是 cur為葉子節點 
				q->plchild=cur->plchild; //重接 q的左子樹
			delete cur;
		}
	}
}

// 列印原始陣列
void PrintArray(int a[],int len)
{	
	for(int i=0;i<len;i++)
		printf("%d ",a[i]);
	printf("\n");
}
int main()
{
	int a[]={50,30,70,10,40,90,80};
	int len=sizeof(a)/sizeof(int);
	BSTreeNode *RootNode=NULL;
	CreateBSTree(RootNode,a,len);
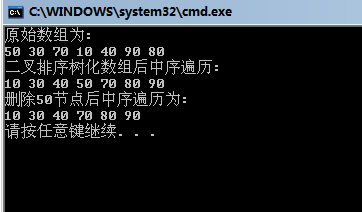
	puts("原始陣列為:");
	PrintArray(a,len);
	puts("二叉排序樹化陣列後中序遍歷:");
	LDR_BiTreeTraverse(RootNode);
	printf("\n");
	//bool i=SearchBST(RootNode,80);
	//i==1 ? printf("80 YES find \n"):printf("80 NO find \n");
	BSTreeNode *DeleposNode=SearchBST(RootNode,50);
	DeleteNode(DeleposNode);
	puts("刪除50節點後中序遍歷為:");
	LDR_BiTreeTraverse(RootNode);
	printf("\n");
	delete RootNode;
}