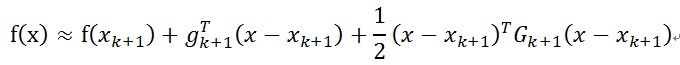最優化之無約束優化

轉自：http://blog.csdn.net/mytestmy/article/details/16903537

1.1問題定義

1.1.1優化問題定義

最優化問題數學上定義，最優化問題的一般形式為

$\begin{array}{l}\min f(x)\\s.t.{\rm{ }}x \in X\end{array}$ （1）

其中的 ${\rm{x}} \in {R^n}$ 是自變數，f(x)是目標函式， ${\rm{X}} \subset {R^n}$ 為約束集或者說可行域。

可行域這個東西，有等式約束，也有不等式約束，或者沒有約束，這次的精力主要還是集中在無約束的優化問題上，如果有精力，再討論有約束的。

1.1.2最優化方法定義

優化問題的解法叫最優化方法。
最優化方法通常採用迭代的方法求它的最優解，其基本思想是：給定一個初始點 ${{\rm{x}}_0} \in {R^n}$ 。按照某一迭代規則產生一個點列 $\left\{ {{x_k}} \right\}$ ，使得當 $\left\{ {{x_k}} \right\}$ 是有窮點列時，其最後一個點是最優化模型問題的最優解，當是 $\left\{ {{x_k}} \right\}$ 無窮點列時，它有極限點，且其極限點是最優化模型問題的最優解。一個好的演算法應具備的典型特徵為：迭代點 ${x_k}$ 能穩定地接近區域性極小值點 ${{\rm{x}}^*}$ 的鄰域，然後迅速收斂於 ${{\rm{x}}^*}$ 。當給定的某個收斂準則滿足時，迭代即終止。

好吧，上面是一堆描述，來點定義，設 ${x_k}$ 為第k次迭代點， ${{\rm{d}}_k}$ 第k次搜尋方向， ${\alpha _k}$ 為第k次步長因子，則第k次迭代為

${x_{k + 1}} = {x_k} + {\alpha _k}{d_k}$ （2）

然後後面的工作幾乎都在調整 ${\alpha _k}{d_k}$ 這個項了，不同的步長 ${\alpha _k}$ 和不同的搜尋方向 ${{\rm{d}}_k}$ 分別構成了不同的方法。

當然步長 ${\alpha _k}$ 和搜尋方向 ${{\rm{d}}_k}$ 是得滿足一些條件，畢竟是求最小值，不能越迭代越大了，下面是一些條件

$\nabla {\rm{f}}{\left( {{x_k}} \right)^T}{d_k} < 0$ （3）

${\rm{f}}\left( {{x_k} + {\alpha _k}{d_k}} \right) < {\rm{f}}\left( {{x_k}} \right)$ （4）

式子（3）的意義是搜尋方向必須跟梯度方向（梯度也就是 $\nabla {\rm{f}}\left( {{x_k}} \right)$ ）夾角大於90度，也就是基本保證是向梯度方向的另外一邊搜尋，至於為什麼要向梯度方向的另外一邊搜尋，就是那樣才能保證是向目標函式值更小的方向搜尋的，因為梯度方向一般是使目標函式增大的（不增大的情況是目標函式已經到達極值）。

式子（4）的意義就很明顯了，迭代的下一步的目標函式比上一步小。

最優化方法的基本結構為：

給定初始點 ${x_0}$ ，

（a）確定搜尋方向 ${{\rm{d}}_k}$ ，即按照一定規則，構造目標函式f在 ${x_k}$ 點處的下降方向作為搜尋方向。

（b）確定步長因子 ${\alpha _k}$ ，使目標函式值有某種意義的下降。

（c）令 ${x_{k + 1}} = {x_k} + {\alpha _k}{d_k}$

若 ${x_{k + 1}}$ 滿足某種終止條件，則停止迭代，得到近似最優解 ${x_{k + 1}}$ ，否則，重複以上步驟。

能不能收斂到最優解是衡量最優化演算法的有效性的一個重要方面。

1.1.3收斂速度簡介

收斂速度也是衡量最優化方法有效性的一個重要方面。

設演算法產生的迭代點列 $\left\{ {{x_k}} \right\}$ 在某種範數意義下收斂，即

${\lim }\limits_{{\rm{k}} \to {\rm{\infty }}} {x_k} - {x^*} = 0$ （5）

若存在實數 ${\rm{\alpha }} > 0$ （這個 ${\rm{\alpha }}$ 不是步長）以及一個與迭代次數k無關的常數 ${\rm{q}} > 0$ ，使得

${\lim }\limits_{{\rm{k}} \to {\rm{\infty }}} \frac{{{x_{k + 1}} - {x^*}}}{{{x_k} - {x^*}^\alpha }} = {\rm{q}}$ （6）

則稱演算法產生的迭代點列 $\left\{ {{x_k}} \right\}$ 具有 ${\rm{Q}} - {\rm{\alpha }}$ 階收斂速度。特別地，常用的說法有以下幾種。

（a）當 ${\rm{\alpha }} = 0$ ， ${\rm{q}} > 0$ 時，迭代點列 $\left\{ {{x_k}} \right\}$ 叫做具有Q-線性收斂速度；

（b）當 $1 < {\rm{\alpha }} < 2$ ，q>0時或 ${\rm{\alpha }} = 1$ ，q=0時，迭代點列 $\left\{ {{x_k}} \right\}$ 叫做具有Q-超線性收斂速度；

（c）當 ${\rm{\alpha }} = 2$ 時，迭代點列 $\left\{ {{x_k}} \right\}$ 叫做具有Q-二階收斂速度；

還有一種叫做R-收斂速度，不討論了，有興趣可以查閱相關資料。

一般認為，具有超線性收斂速度和二階收斂速度的方法是比較快速的。但是對於一個演算法，收斂性和收斂速度的理論結果並不保證演算法在實際執行時一定有好的實際計算特性。一方面是由於這些結果本身並不能保證方法一定有好的特性，另一方面是由於演算法忽略了計算過程中十分重要的舍入誤差的影響。

1.2步長確定

1.2.1一維搜尋

如前面的討論，優化方法的關鍵是構造搜尋方向 ${{\rm{d}}_k}$ 和步長因子 ${\alpha _k}$ ，這一節就討論如何確定步長。

設

${\rm{\varphi }}\left( {\rm{\alpha }} \right) = {\rm{f}}\left( {{x_k} + \alpha {d_k}} \right)$

這樣，從x_k出發，沿搜尋方向 ${{\rm{d}}_k}$ ，確定步長因子 ${\alpha _k}$ ，使得

${\rm{\varphi }}\left( {{\alpha _k}} \right) < {\rm{\varphi }}\left( 0 \right)$

的問題就是關於α的一維搜尋問題。注意這裡是假設其他的 ${x_k}$ 和 ${{\rm{d}}_k}$ 都確定了的情況下做的搜尋，要搜尋的變數只有α。
如果求得的 ${\alpha _k}$ ，使得目標函式沿搜尋方向 ${{\rm{d}}_k}$ 達到最小，即達到下面的情況

${\rm{f}}\left( {{x_k} + {\alpha _k}{d_k}} \right) = {\min }\limits_{\alpha > 0} f\left( {{x_k} + \alpha {d_k}} \right)$

或者說

${\rm{\varphi }}\left( {{\alpha _k}} \right) = {\min }\limits_{\alpha > 0} \varphi \left( \alpha \right)$

如果能求導這個最優的 ${\alpha _k}$ ，那麼這個 ${\alpha _k}$ 就稱為最優步長因子，這樣的搜尋方法就稱為最優一維搜尋，或者精確一維搜尋。
但是現實情況往往不是這樣，實際計算中精確的最優步長因子一般比較難求，工作量也大，所以往往會折中用不精確的一維搜尋。
不精確的一維搜尋，也叫近似一維搜尋。方法是選擇 ${\alpha _k}$ ，使得目標函式f得到可接受的下降量，即使得下降量 ${\rm{f}}\left( {{x_k}} \right) - {\rm{f}}\left( {{x_k} + {\alpha _k}{d_k}} \right) > 0$ 是使用者可接受的。也就是，只要找到一個步長，使得目標函式下降了一個比較滿意的量就可以了。
為啥要選步長？看下圖，步長選不好，方向哪怕是對的，也是跑來跑去，不往下走，二維的情況簡單點，高維的可能會弄出一直原地不動的情況來。

一維搜尋的主要結構如下：1）首先確定包含問題最優解的搜尋區間，再採用某種分割技術或插值方法縮小這個區間，進行搜尋求解。

當然這個搜尋方法主要是適應單峰區間的，就是類似上面的那種，只有一個谷底的。

1.2.1.1確定搜尋區間

確定搜尋區間一般用進退法，思想是從某一點出發，按某步長，確定函式值呈現“高-低-高”的三個點，一個方向不成功，就退回來，沿相反方向尋找。

下面是步驟。

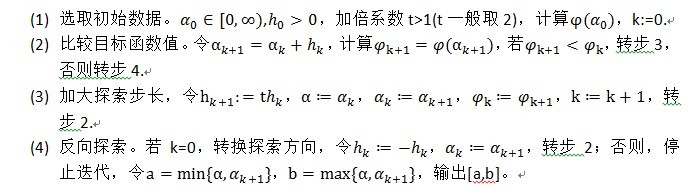
1.2.1.2搜尋求解

搜尋求解的話，0.618法簡單實用。雖然Fibonacci法，插值法等等雖然好，複雜，就不多說了。下面是0.618法的步驟。

普通的0.618法要求一維搜尋的函式是單峰函式，實際上遇到的函式不一定是單峰函式，這時，可能產生搜尋得到的函式值反而大於初始區間端點出函式值的情況。有人建議每次縮小區間是，不要只比較兩個內點處的函式值，而是比較兩內點和兩端點處的函式值。當左邊第一個或第二個點是這四個點中函式值最小的點是，丟棄右端點，構成新的搜尋區間；否則，丟棄左端點，構成新的搜尋區間，經過這樣的修改，演算法會變得可靠些。步驟就不列了。

1.2.2不精確一維搜尋方法

一維搜尋過程是最優化方法的基本組成部分，精確的一維搜尋方法往往需要花費很大的工作量。特別是迭代點遠離問題的解時，精確地求解一個一維子問題通常不是十分有效的。另外，在實際上，很多最優化方法，例如牛頓法和擬牛頓法，其收斂速度並不依賴於精確一維搜尋過程。因此，只要保證目標函式f(x)在每一步都有滿意的下降，這樣就可以大大節省工作量。

有幾位科學家Armijo(1966)和Goldstein(1965)分別提出了不精確一維搜尋過程。設

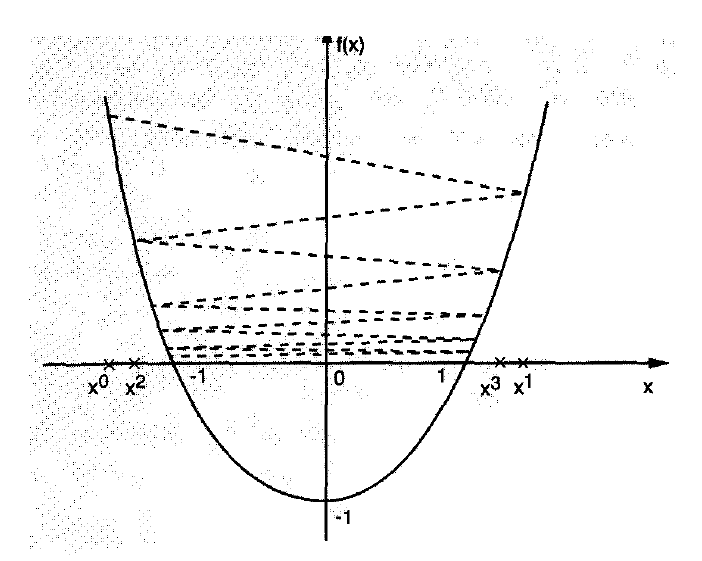
${\rm{J}} = \{ {\rm{\alpha }} > 0|{\rm{f}}\left( {{x_k} + \alpha {d_k}} \right) < {\rm{f}}\left( {{x_k}} \right)\}$ （2.5.1）

是一個區間。看下圖

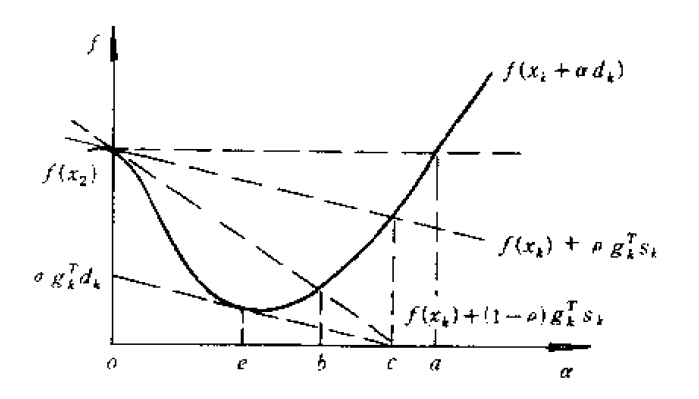
在圖中，區間J=(0,a)。為了保證目標函式單調下降，同時要求f的下降不是太小（如果f的下降太小，可能導致序列 $\left\{ {{\rm{f}}\left( {{x_k}} \right)} \right\}$ 的極限值不是極小值），必須避免所選擇的α太靠近區間j的短短。一個合理的要求是

${\rm{f}}\left( {{x_k} + {s_k}} \right) \le {\rm{f}}\left( {{x_k}} \right) + \rho g_k^T{s_k}$ （2.5.2）

${\rm{f}}\left( {{x_k} + {s_k}} \right) \ge {\rm{f}}\left( {{x_k}} \right) + \left( {1 - \rho } \right)g_k^T{s_k}$ （2.5.3）

其中0<ρ<1/2， ${s_k} = {\alpha _k}{d_k}$ 。滿足(2.5.2)要求的α_k構成區間J_1=(0,c]，這就扔掉了區間J右端附件的點。但是為了避免α太小的情況，又加上了另一個要求(2.5.3)，這個要求扔掉了區間J的左端點附件的點。看圖中 ${\rm{f}}\left( {{x_k}} \right) + \rho g_k^T{s_k}$ 和 ${\rm{f}}\left( {{x_k}} \right) + \left( {1 - \rho } \right)g_k^T{s_k}$ 兩條虛線夾出來的區間J_2=[b,c]就是滿足條件(2.5.2)和(2.5.3)的搜尋區間，稱為可接受區間。條件(2.5.2)和(2.5.3)稱為Armijo-Goldstein準則。無論用什麼辦法得到步長因子α，只要滿足條件(2.5.2)和(2.5.3)，就可以稱它為可接受步長因子。

其中這個要求是必須的，因為不用這個條件，可能會影響牛頓法和擬牛頓法的超線性收斂。

在圖中可以看到一種情況，極小值e也被扔掉了，為了解決這種情況，Wolfe-Powell準則給出了一個更簡單的條件代替

$g_{k + 1}^T{d_k} \ge \sigma g_k^T{d_k},{\rm{\sigma }} \in \left( {{\rm{\rho }},1} \right)$ （2.5.4）

其幾何解釋是在可接受點處切線的斜率 $\varphi '\left( {{\alpha _k}} \right)$ 大於或等於初始斜率的σ倍。準則(2.5.2)和(2.5.4)稱為Wolfe-Powell準則，其可接受區間為J_3=[e,c]。

要求ρ<σ<1是必要的，它保證了滿足不精確線性搜尋準則的步長因子 ${\alpha _k}$ 的存在，不這麼弄，可能 $\sigma g_k^T{d_k}$ 這個虛線會往下壓，沒有交點，就搞不出一個區間來了。

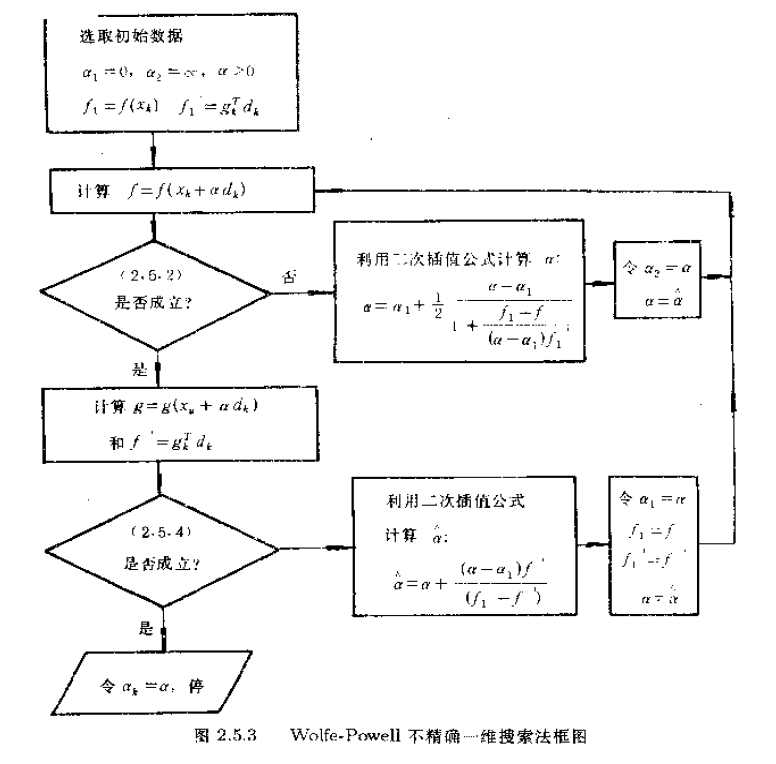
一般地，σ值越小，線性搜尋越精確。取σ=0.1，就得到一個相當精確的線性搜尋，而取σ=0.9，則得到一個相當弱的線性搜尋。不過σ值越小，工作量越大。所以不精確線性搜尋不要求過小的σ，通常可取ρ=0.1，σ=0.4。

下面就給出Armijo-Goldstein準則和Wolfe-Powell準則的框圖。

從演算法框圖中可以看出，兩種方法是類似的，只是在準則不成立，需要計算新的時，一個利用了簡單的求區間中點的方法，另一個採用了二次插值方法。

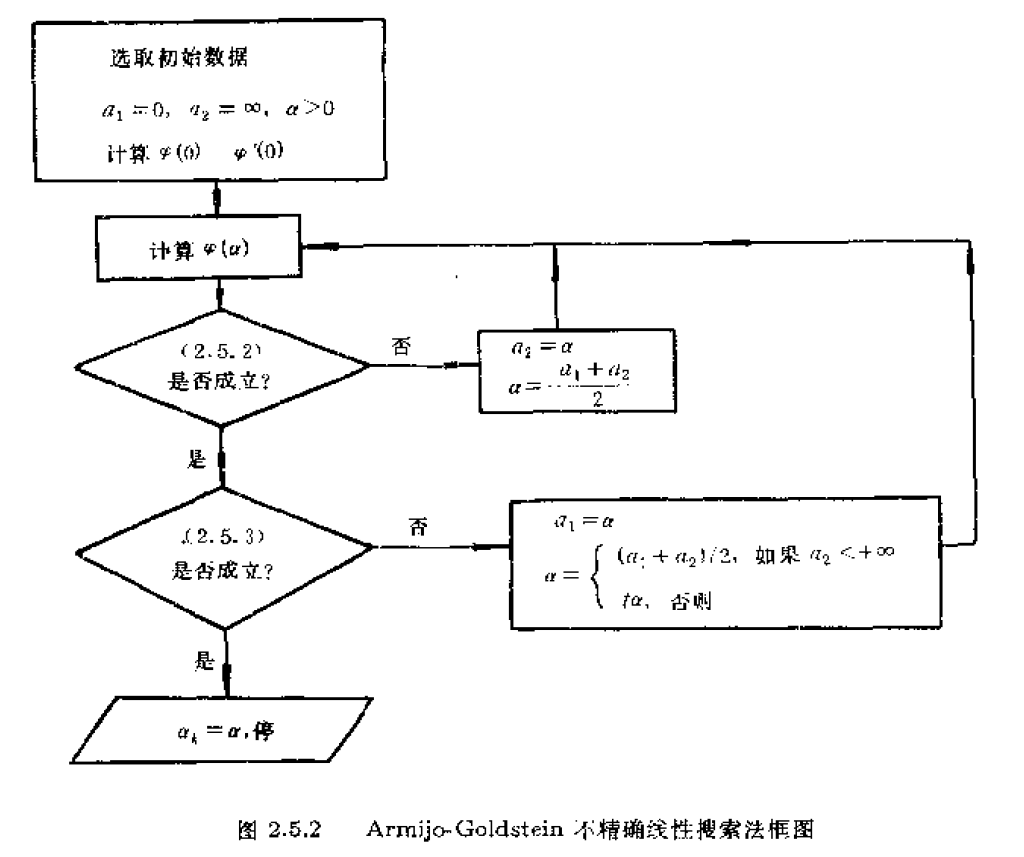
演算法步驟只給出Armijo-Goldstein不精確一維搜尋方法的，下面就是

好了，說到這，確定步長的方法也說完了，其實方法不少，實際用到的肯定是最簡單的幾種，就把簡單的幾種提了一下，至於為什麼這樣，收斂如何，證明的東西大家可以去書中慢慢看。

1.3方向確定

1.3.1最速下降法

最速下降法以負梯度方向作為最優化方法的下降方向，又稱為梯度下降法，是最簡單實用的方法。

1.3.1.1演算法步驟

下面是步驟。

看個例子。

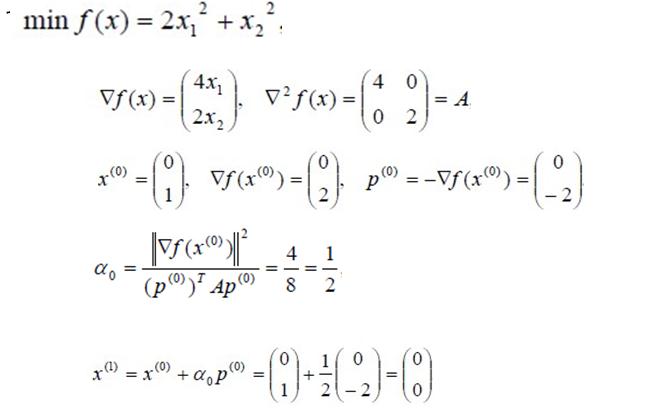
這個選步長的方法是對二次函式下的特殊情況，是比較快而且好的顯式形式，說明步長選得好，收斂很快。

1.3.1.2缺點

數值實驗表明，當目標函式的等值線接近一個圓（球）時，最速下降法下降較快，當目標函式的等值線是一個扁長的橢球是，最速下降法開始幾步下降較快，後來就出現鋸齒線性，下降就十分緩慢。原因是一維搜尋滿足 $g_{k + 1}^T{d_k} = 0$ ，即 $g_{k + 1}^T{g_k} = d_{k + 1}^T{d_k} = 0$ ，這表明在相鄰兩個迭代點上函式f(x)的兩個梯度繁星是互相直交（正交）的。即，兩個搜尋方向互相直交，就產生了鋸齒性質。當接近極小點時，步長越小，前進越慢。
下圖是鋸齒的一個圖。

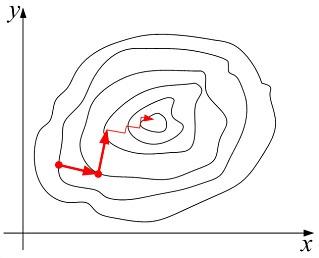
1.3.2牛頓法

1.3.2.1演算法思想和步驟

牛頓法的基本思想是利用目標函式的二次Taylor展開，並將其極小化。
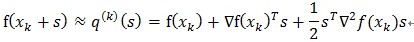
設f(x)是二次可微實函式， ${x_k} \in {{\rm{R}}^n}$ ，Hesse矩陣 ${\nabla ^2}f\left( {{x_k}} \right)$ 正定。在 ${x_k}$ 附件用二次Taylor展開近似f，

其中， $s = {\rm{x}} - {x_k}$ ， ${q^{\left( k \right)}}\left( s \right)$ 為f(x)的二次近似。將上式右邊極小化，便得
${x_{k + 1}} = {x_k} - {\left[ {{\nabla ^2}f\left( {{x_k}} \right)} \right]^{ - 1}}\nabla {\rm{f}}\left( {{x_k}} \right)$

這就是牛頓迭代公式。在這個公式中，步長因子 ${\alpha _k} = 1$ 。令 ${G_k} = {\nabla ^2}f\left( {{x_k}} \right) = H(f)$ , ${g_k} = \nabla {\rm{f}}\left( {{x_k}} \right)$ ，則上面的迭代式也可以寫成 ${x_{k + 1}} = {x_k} - {\rm{G}}_k^{ - 1}{g_k}$ 。

其中的Hesse矩陣的形式如下。

一個例子如下。

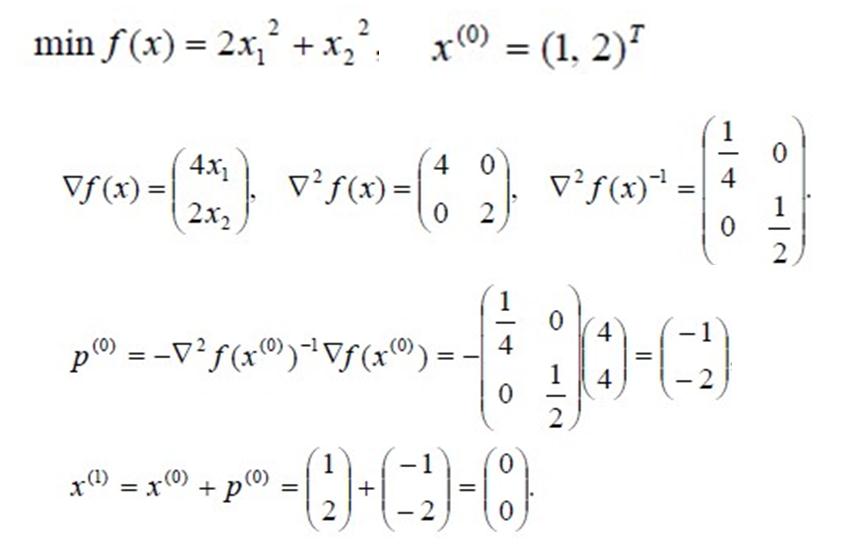
對於正定二次函式，牛頓法一步就可以得到最優解。
對於非二次函式，牛頓法並不能保證經過有限次迭代求得最優解，但由於目標函式在極小點附近近似於二次函式，所以當初始點靠近極小點時，牛頓法的收斂速度一般是快的。
當初始點遠離最優解， ${G_k}$ 不一定正定，牛頓方向不一定是下降方向，其收斂性不能保證，這說明步長一直是1是不合適的，應該在牛頓法中採用某種一維搜尋來確定步長因子。但是要強調一下，僅當步長因子 $\{ {\alpha _k}\}$ 收斂到1時，牛頓法才是二階收斂的。
這時的牛頓法稱為阻尼牛頓法，步驟如下。

下面看個例子。

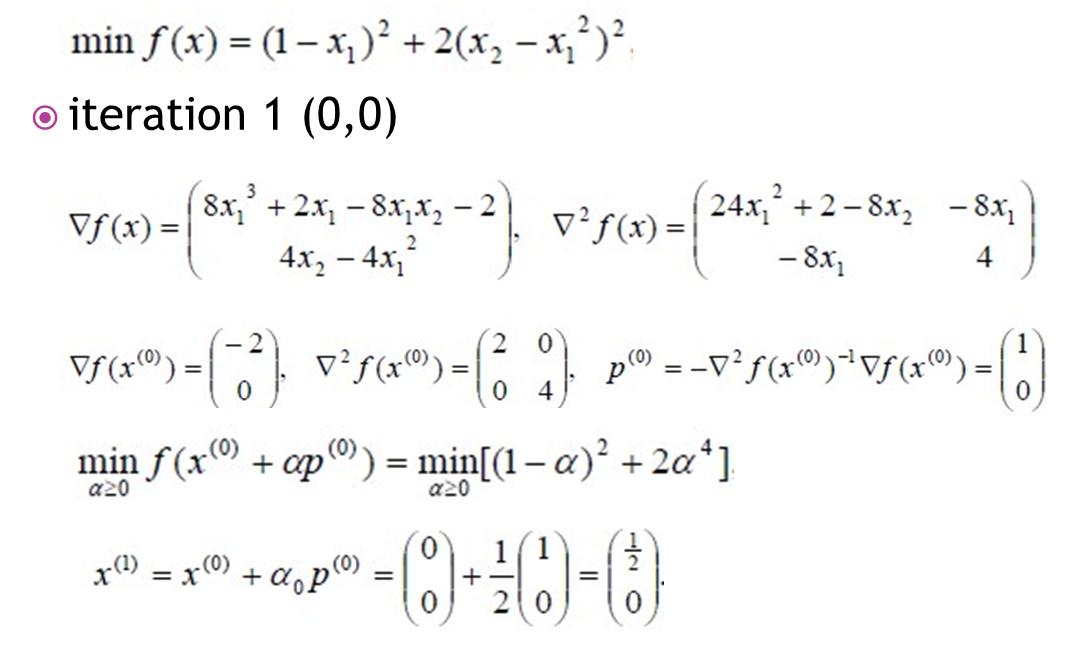
這樣的牛頓法是總體收斂的。

1.3.2.2缺點

牛頓法面臨的主要困難是Hesse矩陣 ${G_k}$ 不正定。這時候二次模型不一定有極小點，甚至沒有平穩點。當 ${G_k}$ 不正定時，二次模型函式是無界的。
為了克服這種困難，有多種方法，常用的方法是使牛頓方向偏向最速下降方向 $- {g_k}$ 。具體做法是將Hesse矩陣 ${G_k}$ 改變成 ${{\rm{G}}_k} + {\nu _k}I$ ，其中 ${\nu _k} > 0$ ，使得 ${{\rm{G}}_k} + {\nu _k}I$ 正定。 ${\nu _k}$ 一般希望是比較小，最好是剛剛好能使 ${{\rm{G}}_k} + {\nu _k}I$ 正定。

1.3.3擬牛頓法

牛頓法在實際應用中需要儲存二階導數資訊和計算一個矩陣的逆，這對計算機的時間和空間要求都比較高，也容易遇到不正定的Hesse矩陣和病態的Hesse矩陣，導致求出來的逆很古怪，從而演算法會沿一個不理想的方向去迭代。

有人提出了介於最速下降法與牛頓法之間的方法。一類是共軛方向法，典型的是共軛梯度法，還有擬牛頓法。

其中擬牛頓法簡單實用，這裡就特地介紹，其他方法感興趣的讀者可以去看相關資料。

1.3.3.1演算法思想和步驟

牛頓法的成功的關鍵是利用了Hesse矩陣提供的曲率資訊。但是計算Hesse矩陣工作量大，並且有些目標函式的Hesse矩陣很難計算，甚至不好求出，這就使得僅利用目標函式的一階導數的方法更受歡迎。擬牛頓法就是利用目標函式值f和一階導數g（梯度）的資訊，構造出目標函式的曲率近似，而不需要明顯形成Hesse矩陣，同時具有收斂速度快的特點。
設 ${\rm{f}}:{R^n} \to R$ 在開集 ${\cal D} \subset {{\rm{R}}^n}$ 上二次可微，f在 ${x_{k + 1}}$ 附近的二次近似為

兩邊求導，得

${\rm{g}}\left( {\rm{x}} \right) \approx {g_{k + 1}} + {G_{k + 1}}\left( {x - {x_{k + 1}}} \right)$

令 $x = {x_k},{s_k} = {x_{k + 1}} - {x_k},{y_k} = {g_{k + 1}} - {g_k}$ ，得 $G_{k + 1}^{ - 1}{y_k} \approx {s_k}$

其中 ${g_k} = \nabla f\left( {{x_k}} \right) \ne 0$ ，是梯度。那麼，只要構造出Hesse矩陣的逆近似 ${{\rm{H}}_{k + 1}}$ 滿足這種上式就可以，即滿足關係

${{\rm{H}}_{k + 1}}{y_k} = {s_k}$

這個關係就是擬牛頓條件或擬牛頓方程。
擬牛頓法的思想就是——用一個矩陣 ${{\rm{H}}_k}$ 去近似Hesse矩陣的逆矩陣，這樣就避免了計算矩陣的逆。
當然 ${{\rm{H}}_k}$ 需要滿足一些條件：

(a) ${{\rm{H}}_k}$ 是一個正定的矩陣

(b) 如果 ${\nabla ^2}f{\left( {{x_k}} \right)^{ - 1}}$ 存在，則 ${{\rm{H}}_k} \approx {\nabla ^2}f{\left( {{x_k}} \right)^{ - 1}}$ 。

(c) 初始正定矩陣 ${{\rm{H}}_0}$ 取定後， ${{\rm{H}}_{k + 1}}$ 應該由 ${{\rm{H}}_k}$ 遞推給出，即 ${{\rm{H}}_{k + 1}} = {{\rm{H}}_k} + {{\rm{E}}_k}$ ；其中 ${{\rm{E}}_k}$ 是修正矩陣， ${{\rm{H}}_{k + 1}} = {{\rm{H}}_k} + {{\rm{E}}_k}$ 是修正公式。

常用而且有效的修正公式是BFGS公式，如下

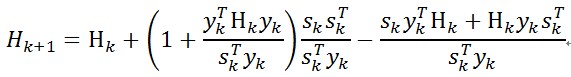
下面給出BFGS公式下的擬牛頓法

在上述步驟中，初始正定矩陣 ${{\rm{H}}_0}$ 通常取為單位矩陣，即 ${{\rm{H}}_0} = {\rm{I}}$ 。這樣，擬牛頓法的第一次迭代相當於一個最速下降迭代。

1.3.3.2優缺點

與牛頓法相比，有兩個優點：

(a) 僅需一階導數

(b) 校正保持正定性，因而下降性質成立

(c) 無需計算逆矩陣，但具有超線性收斂速度

(d) 每次迭代僅需要次乘法計算

缺點是初始點距離最優解遠時速度還是慢。

解決方法是，迭代前期用最速下降法進行迭代，得到一定解以後用擬牛頓法迭代。

1.1問題定義

1.1.1優化問題定義

最優化問題數學上定義，最優化問題的一般形式為

$\begin{array}{l}\min f(x)\\s.t.{\rm{ }}x \in X\end{array}$ （1）

其中的 ${\rm{x}} \in {R^n}$ 是自變數，f(x)是目標函式， ${\rm{X}} \subset {R^n}$ 為約束集或者說可行域。

可行域這個東西，有等式約束，也有不等式約束，或者沒有約束，這次的精力主要還是集中在無約束的優化問題上，如果有精力，再討論有約束的。

1.1.2最優化方法定義

優化問題的解法叫最優化方法。
最優化方法通常採用迭代的方法求它的最優解，其基本思想是：給定一個初始點 ${{\rm{x}}_0} \in {R^n}$ 。按照某一迭代規則產生一個點列 $\left\{ {{x_k}} \right\}$ ，使得當 $\left\{ {{x_k}} \right\}$ 是有窮點列時，其最後一個點是最優化模型問題的最優解，當是 $\left\{ {{x_k}} \right\}$ 無窮點列時，它有極限點，且其極限點是最優化模型問題的最優解。一個好的演算法應具備的典型特徵為：迭代點 ${x_k}$ 能穩定地接近區域性極小值點 ${{\rm{x}}^*}$ 的鄰域，然後迅速收斂於 ${{\rm{x}}^*}$ 。當給定的某個收斂準則滿足時，迭代即終止。

好吧，上面是一堆描述，來點定義，設 ${x_k}$ 為第k次迭代點， ${{\rm{d}}_k}$ 第k次搜尋方向， ${\alpha _k}$ 為第k次步長因子，則第k次迭代為

${x_{k + 1}} = {x_k} + {\alpha _k}{d_k}$ （2）

然後後面的工作幾乎都在調整 ${\alpha _k}{d_k}$ 這個項了，不同的步長 ${\alpha _k}$ 和不同的搜尋方向 ${{\rm{d}}_k}$ 分別構成了不同的方法。

當然步長 ${\alpha _k}$ 和搜尋方向 ${{\rm{d}}_k}$ 是得滿足一些條件，畢竟是求最小值，不能越迭代越大了，下面是一些條件

$\nabla {\rm{f}}{\left( {{x_k}} \right)^T}{d_k} < 0$ （3）

${\rm{f}}\left( {{x_k} + {\alpha _k}{d_k}} \right) < {\rm{f}}\left( {{x_k}} \right)$ （4）

式子（3）的意義是搜尋方向必須跟梯度方向（梯度也就是 $\nabla {\rm{f}}\left( {{x_k}} \right)$ ）夾角大於90度，也就是基本保證是向梯度方向的另外一邊搜尋，至於為什麼要向梯度方向的另外一邊搜尋，就是那樣才能保證是向目標函式值更小的方向搜尋的，因為梯度方向一般是使目標函式增大的（不增大的情況是目標函式已經到達極值）。

式子（4）的意義就很明顯了，迭代的下一步的目標函式比上一步小。

最優化方法的基本結構為：

給定初始點 ${x_0}$ ，

（a）確定搜尋方向 ${{\rm{d}}_k}$ ，即按照一定規則，構造目標函式f在 ${x_k}$ 點處的下降方向作為搜尋方向。

（b）確定步長因子 ${\alpha _k}$ ，使目標函式值有某種意義的下降。

（c）令 ${x_{k + 1}} = {x_k} + {\alpha _k}{d_k}$

若 ${x_{k + 1}}$ 滿足某種終止條件，則停止迭代，得到近似最優解 ${x_{k + 1}}$ ，否則，重複以上步驟。

能不能收斂到最優解是衡量最優化演算法的有效性的一個重要方面。

1.1.3收斂速度簡介

收斂速度也是衡量最優化方法有效性的一個重要方面。

設演算法產生的迭代點列 $\left\{ {{x_k}} \right\}$ 在某種範數意義下收斂，即

${\lim }\limits_{{\rm{k}} \to {\rm{\infty }}} {x_k} - {x^*} = 0$ （5）

若存在實數 ${\rm{\alpha }} > 0$ （這個 ${\rm{\alpha }}$ 不是步長）以及一個與迭代次數k無關的常數 ${\rm{q}} > 0$ ，使得

${\lim }\limits_{{\rm{k}} \to {\rm{\infty }}} \frac{{{x_{k + 1}} - {x^*}}}{{{x_k} - {x^*}^\alpha }} = {\rm{q}}$ （6）

則稱演算法產生的迭代點列 $\left\{ {{x_k}} \right\}$ 具有 ${\rm{Q}} - {\rm{\alpha }}$ 階收斂速度。特別地，常用的說法有以下幾種。

（a）當 ${\rm{\alpha }} = 0$ ， ${\rm{q}} > 0$ 時，迭代點列 $\left\{ {{x_k}} \right\}$ 叫做具有Q-線性收斂速度；

（b）當 $1 < {\rm{\alpha }} < 2$ ，q>0時或 ${\rm{\alpha }} = 1$ ，q=0時，迭代點列 $\left\{ {{x_k}} \right\}$ 叫做具有Q-超線性收斂速度；

（c）當 ${\rm{\alpha }} = 2$ 時，迭代點列 $\left\{ {{x_k}} \right\}$ 叫做具有Q-二階收斂速度；

還有一種叫做R-收斂速度，不討論了，有興趣可以查閱相關資料。

一般認為，具有超線性收斂速度和二階收斂速度的方法是比較快速的。但是對於一個演算法，收斂性和收斂速度的理論結果並不保證演算法在實際執行時一定有好的實際計算特性。一方面是由於這些結果本身並不能保證方法一定有好的特性，另一方面是由於演算法忽略了計算過程中十分重要的舍入誤差的影響。

1.2步長確定

1.2.1一維搜尋

如前面的討論，優化方法的關鍵是構造搜尋方向 ${{\rm{d}}_k}$ 和步長因子 ${\alpha _k}$ ，這一節就討論如何確定步長。

設

${\rm{\varphi }}\left( {\rm{\alpha }} \right) = {\rm{f}}\left( {{x_k} + \alpha {d_k}} \right)$

這樣，從x_k出發，沿搜尋方向 ${{\rm{d}}_k}$ ，確定步長因子 ${\alpha _k}$ ，使得

${\rm{\varphi }}\left( {{\alpha _k}} \right) < {\rm{\varphi }}\left( 0 \right)$

的問題就是關於α的一維搜尋問題。注意這裡是假設其他的 ${x_k}$ 和 ${{\rm{d}}_k}$ 都確定了的情況下做的搜尋，要搜尋的變數只有α。
如果求得的 ${\alpha _k}$ ，使得目標函式沿搜尋方向 ${{\rm{d}}_k}$ 達到最小，即達到下面的情況

${\rm{f}}\left( {{x_k} + {\alpha _k}{d_k}} \right) = {\min }\limits_{\alpha > 0} f\left( {{x_k} + \alpha {d_k}} \right)$

或者說

${\rm{\varphi }}\left( {{\alpha _k}} \right) = {\min }\limits_{\alpha > 0} \varphi \left( \alpha \right)$

如果能求導這個最優的 ${\alpha _k}$ ，那麼這個 ${\alpha _k}$ 就稱為最優步長因子，這樣的搜尋方法就稱為最優一維搜尋，或者精確一維搜尋。
但是現實情況往往不是這樣，實際計算中精確的最優步長因子一般比較難求，工作量也大，所以往往會折中用不精確的一維搜尋。
不精確的一維搜尋，也叫近似一維搜尋。方法是選擇 ${\alpha _k}$ ，使得目標函式f得到可接受的下降量，即使得下降量 ${\rm{f}}\left( {{x_k}} \right) - {\rm{f}}\left( {{x_k} + {\alpha _k}{d_k}} \right) > 0$ 是使用者可接受的。也就是，只要找到一個步長，使得目標函式下降了一個比較滿意的量就可以了。
為啥要選步長？看下圖，步長選不好，方向哪怕是對的，也是跑來跑去，不往下走，二維的情況簡單點，高維的可能會弄出一直原地不動的情況來。

一維搜尋的主要結構如下：1）首先確定包含問題最優解的搜尋區間，再採用某種分割技術或插值方法縮小這個區間，進行搜尋求解。

當然這個搜尋方法主要是適應單峰區間的，就是類似上面的那種，只有一個谷底的。

1.2.1.1確定搜尋區間

確定搜尋區間一般用進退法，思想是從某一點出發，按某步長，確定函式值呈現“高-低-高”的三個點，一個方向不成功，就退回來，沿相反方向尋找。

下面是步驟。

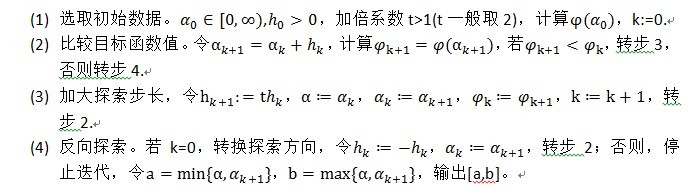
1.2.1.2搜尋求解

搜尋求解的話，0.618法簡單實用。雖然Fibonacci法，插值法等等雖然好，複雜，就不多說了。下面是0.618法的步驟。

普通的0.618法要求一維搜尋的函式是單峰函式，實際上遇到的函式不一定是單峰函式，這時，可能產生搜尋得到的函式值反而大於初始區間端點出函式值的情況。有人建議每次縮小區間是，不要只比較兩個內點處的函式值，而是比較兩內點和兩端點處的函式值。當左邊第一個或第二個點是這四個點中函式值最小的點是，丟棄右端點，構成新的搜尋區間；否則，丟棄左端點，構成新的搜尋區間，經過這樣的修改，演算法會變得可靠些。步驟就不列了。

1.2.2不精確一維搜尋方法

一維搜尋過程是最優化方法的基本組成部分，精確的一維搜尋方法往往需要花費很大的工作量。特別是迭代點遠離問題的解時，精確地求解一個一維子問題通常不是十分有效的。另外，在實際上，很多最優化方法，例如牛頓法和擬牛頓法，其收斂速度並不依賴於精確一維搜尋過程。因此，只要保證目標函式f(x)在每一步都有滿意的下降，這樣就可以大大節省工作量。

有幾位科學家Armijo(1966)和Goldstein(1965)分別提出了不精確一維搜尋過程。設

${\rm{J}} = \{ {\rm{\alpha }} > 0|{\rm{f}}\left( {{x_k} + \alpha {d_k}} \right) < {\rm{f}}\left( {{x_k}} \right)\}$ （2.5.1）

是一個區間。看下圖

在圖中，區間J=(0,a)。為了保證目標函式單調下降，同時要求f的下降不是太小（如果f的下降太小，可能導致序列 $\left\{ {{\rm{f}}\left( {{x_k}} \right)} \right\}$ 的極限值不是極小值），必須避免所選擇的α太靠近區間j的短短。一個合理的要求是

${\rm{f}}\left( {{x_k} + {s_k}} \right) \le {\rm{f}}\left( {{x_k}} \right) + \rho g_k^T{s_k}$ （2.5.2）

${\rm{f}}\left( {{x_k} + {s_k}} \right) \ge {\rm{f}}\left( {{x_k}} \right) + \left( {1 - \rho } \right)g_k^T{s_k}$ （2.5.3）

其中0<ρ<1/2， ${s_k} = {\alpha _k}{d_k}$ 。滿足(2.5.2)要求的α_k構成區間J_1=(0,c]，這就扔掉了區間J右端附件的點。但是為了避免α太小的情況，又加上了另一個要求(2.5.3)，這個要求扔掉了區間J的左端點附件的點。看圖中 ${\rm{f}}\left( {{x_k}} \right) + \rho g_k^T{s_k}$ 和 ${\rm{f}}\left( {{x_k}} \right) + \left( {1 - \rho } \right)g_k^T{s_k}$ 兩條虛線夾出來的區間J_2=[b,c]就是滿足條件(2.5.2)和(2.5.3)的搜尋區間，稱為可接受區間。條件(2.5.2)和(2.5.3)稱為Armijo-Goldstein準則。無論用什麼辦法得到步長因子α，只要滿足條件(2.5.2)和(2.5.3)，就可以稱它為可接受步長因子。

其中這個要求是必須的，因為不用這個條件，可能會影響牛頓法和擬牛頓法的超線性收斂。

在圖中可以看到一種情況，極小值e也被扔掉了，為了解決這種情況，Wolfe-Powell準則給出了一個更簡單的條件代替

$g_{k + 1}^T{d_k} \ge \sigma g_k^T{d_k},{\rm{\sigma }} \in \left( {{\rm{\rho }},1} \right)$ （2.5.4）

其幾何解釋是在可接受點處切線的斜率 $\varphi '\left( {{\alpha _k}} \right)$ 大於或等於初始斜率的σ倍。準則(2.5.2)和(2.5.4)稱為Wolfe-Powell準則，其可接受區間為J_3=[e,c]。

要求ρ<σ<1是必要的，它保證了滿足不精確線性搜尋準則的步長因子 ${\alpha _k}$ 的存在，不這麼弄，可能 $\sigma g_k^T{d_k}$ 這個虛線會往下壓，沒有交點，就搞不出一個區間來了。

一般地，σ值越小，線性搜尋越精確。取σ=0.1，就得到一個相當精確的線性搜尋，而取σ=0.9，則得到一個相當弱的線性搜尋。不過σ值越小，工作量越大。所以不精確線性搜尋不要求過小的σ，通常可取ρ=0.1，σ=0.4。

下面就給出Armijo-Goldstein準則和Wolfe-Powell準則的框圖。

從演算法框圖中可以看出，兩種方法是類似的，只是在準則不成立，需要計算新的時，一個利用了簡單的求區間中點的方法，另一個採用了二次插值方法。

演算法步驟只給出Armijo-Goldstein不精確一維搜尋方法的，下面就是

好了，說到這，確定步長的方法也說完了，其實方法不少，實際用到的肯定是最簡單的幾種，就把簡單的幾種提了一下，至於為什麼這樣，收斂如何，證明的東西大家可以去書中慢慢看。

1.3方向確定

1.3.1最速下降法

最速下降法以負梯度方向作為最優化方法的下降方向，又稱為梯度下降法，是最簡單實用的方法。

1.3.1.1演算法步驟

下面是步驟。

看個例子。

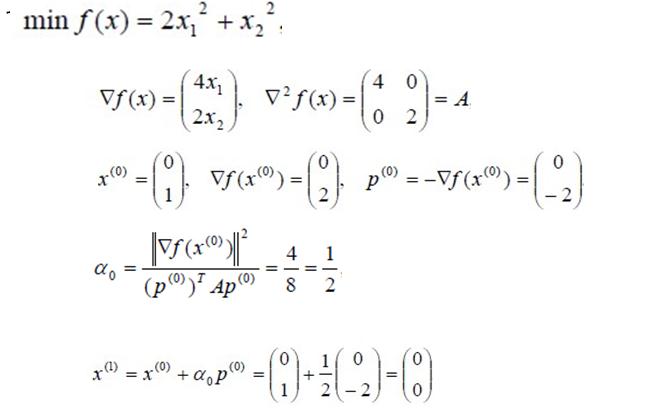
這個選步長的方法是對二次函式下的特殊情況，是比較快而且好的顯式形式，說明步長選得好，收斂很快。

1.3.1.2缺點

數值實驗表明，當目標函式的等值線接近一個圓（球）時，最速下降法下降較快，當目標函式的等值線是一個扁長的橢球是，最速下降法開始幾步下降較快，後來就出現鋸齒線性，下降就十分緩慢。原因是一維搜尋滿足 $g_{k + 1}^T{d_k} = 0$ ，即 $g_{k + 1}^T{g_k} = d_{k + 1}^T{d_k} = 0$ ，這表明在相鄰兩個迭代點上函式f(x)的兩個梯度繁星是互相直交（正交）的。即，兩個搜尋方向互相直交，就產生了鋸齒性質。當接近極小點時，步長越小，前進越慢。
下圖是鋸齒的一個圖。

1.3.2牛頓法

1.3.2.1演算法思想和步驟

牛頓法的基本思想是利用目標函式的二次Taylor展開，並將其極小化。
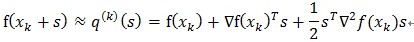
設f(x)是二次可微實函式， ${x_k} \in {{\rm{R}}^n}$ ，Hesse矩陣 ${\nabla ^2}f\left( {{x_k}} \right)$ 正定。在 ${x_k}$ 附件用二次Taylor展開近似f，

其中， $s = {\rm{x}} - {x_k}$ ， ${q^{\left( k \right)}}\left( s \right)$ 為f(x)的二次近似。將上式右邊極小化，便得
${x_{k + 1}} = {x_k} - {\left[ {{\nabla ^2}f\left( {{x_k}} \right)} \right]^{ - 1}}\nabla {\rm{f}}\left( {{x_k}} \right)$

這就是牛頓迭代公式。在這個公式中，步長因子 ${\alpha _k} = 1$ 。令 ${G_k} = {\nabla ^2}f\left( {{x_k}} \right) = H(f)$ , ${g_k} = \nabla {\rm{f}}\left( {{x_k}} \right)$ ，則上面的迭代式也可以寫成 ${x_{k + 1}} = {x_k} - {\rm{G}}_k^{ - 1}{g_k}$ 。

其中的Hesse矩陣的形式如下。

一個例子如下。

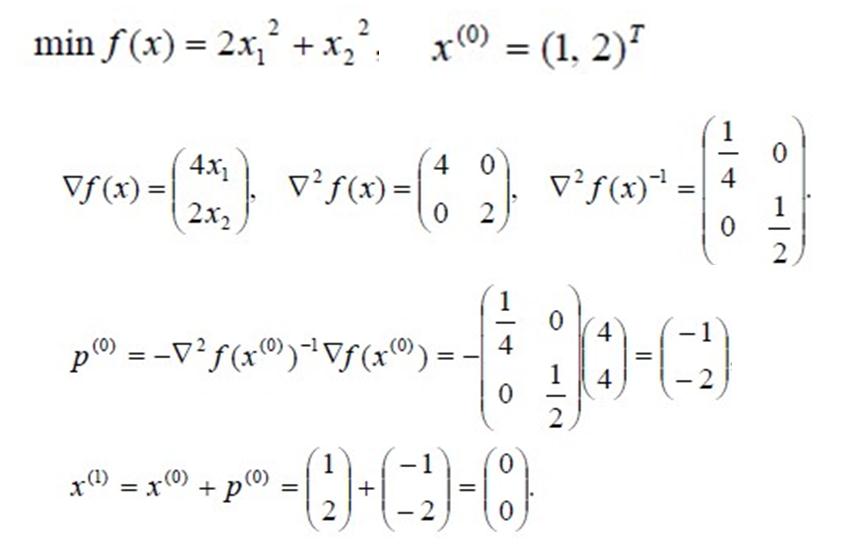
對於正定二次函式，牛頓法一步就可以得到最優解。
對於非二次函式，牛頓法並不能保證經過有限次迭代求得最優解，但由於目標函式在極小點附近近似於二次函式，所以當初始點靠近極小點時，牛頓法的收斂速度一般是快的。
當初始點遠離最優解， ${G_k}$ 不一定正定，牛頓方向不一定是下降方向，其收斂性不能保證，這說明步長一直是1是不合適的，應該在牛頓法中採用某種一維搜尋來確定步長因子。但是要強調一下，僅當步長因子 $\{ {\alpha _k}\}$ 收斂到1時，牛頓法才是二階收斂的。
這時的牛頓法稱為阻尼牛頓法，步驟如下。

下面看個例子。

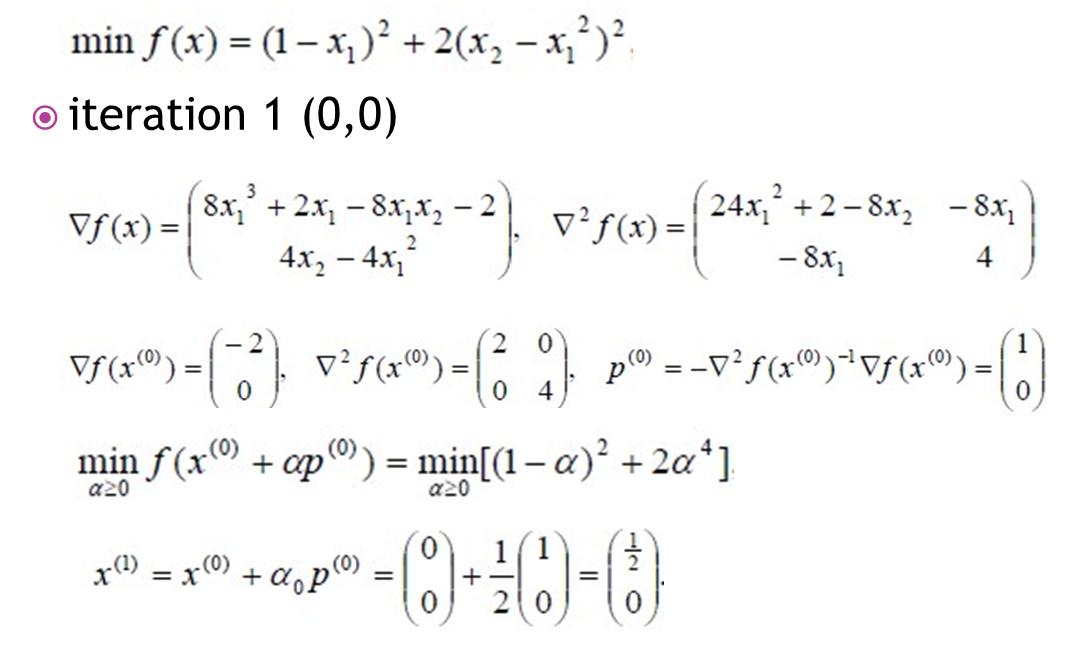
這樣的牛頓法是總體收斂的。

1.3.2.2缺點

牛頓法面臨的主要困難是Hesse矩陣 ${G_k}$ 不正定。這時候二次模型不一定有極小點，甚至沒有平穩點。當 ${G_k}$ 不正定時，二次模型函式是無界的。
為了克服這種困難，有多種方法，常用的方法是使牛頓方向偏向最速下降方向 $- {g_k}$ 。具體做法是將Hesse矩陣 ${G_k}$ 改變成 ${{\rm{G}}_k} + {\nu _k}I$ ，其中 ${\nu _k} > 0$ ，使得 ${{\rm{G}}_k} + {\nu _k}I$ 正定。 ${\nu _k}$ 一般希望是比較小，最好是剛剛好能使 ${{\rm{G}}_k} + {\nu _k}I$ 正定。

1.3.3擬牛頓法

牛頓法在實際應用中需要儲存二階導數資訊和計算一個矩陣的逆，這對計算機的時間和空間要求都比較高，也容易遇到不正定的Hesse矩陣和病態的Hesse矩陣，導致求出來的逆很古怪，從而演算法會沿一個不理想的方向去迭代。

有人提出了介於最速下降法與牛頓法之間的方法。一類是共軛方向法，典型的是共軛梯度法，還有擬牛頓法。

其中擬牛頓法簡單實用，這裡就特地介紹，其他方法感興趣的讀者可以去看相關資料。

1.3.3.1演算法思想和步驟

牛頓法的成功的關鍵是利用了Hesse矩陣提供的曲率資訊。但是計算Hesse矩陣工作量大，並且有些目標函式的Hesse矩陣很難計算，甚至不好求出，這就使得僅利用目標函式的一階導數的方法更受歡迎。擬牛頓法就是利用目標函式值f和一階導數g（梯度）的資訊，構造出目標函式的曲率近似，而不需要明顯形成Hesse矩陣，同時具有收斂速度快的特點。
設 ${\rm{f}}:{R^n} \to R$ 在開集 ${\cal D} \subset {{\rm{R}}^n}$ 上二次可微，f在 ${x_{k + 1}}$ 附近的二次近似為

兩邊求導，得

${\rm{g}}\left( {\rm{x}} \right) \approx {g_{k + 1}} + {G_{k + 1}}\left( {x - {x_{k + 1}}} \right)$

令 $x = {x_k},{s_k} = {x_{k + 1}} - {x_k},{y_k} = {g_{k + 1}} - {g_k}$ ，得 $G_{k + 1}^{ - 1}{y_k} \approx {s_k}$

其中 ${g_k} = \nabla f\left( {{x_k}} \right) \ne 0$ ，是梯度。那麼，只要構造出Hesse矩陣的逆近似 ${{\rm{H}}_{k + 1}}$ 滿足這種上式就可以，即滿足關係

${{\rm{H}}_{k + 1}}{y_k} = {s_k}$

這個關係就是擬牛頓條件或擬牛頓方程。
擬牛頓法的思想就是——用一個矩陣 ${{\rm{H}}_k}$ 去近似Hesse矩陣的逆矩陣，這樣就避免了計算矩陣的逆。
當然 ${{\rm{H}}_k}$ 需要滿足一些條件：

(a) ${{\rm{H}}_k}$ 是一個正定的矩陣

(b) 如果 ${\nabla ^2}f{\left( {{x_k}} \right)^{ - 1}}$ 存在，則 ${{\rm{H}}_k} \approx {\nabla ^2}f{\left( {{x_k}} \right)^{ - 1}}$ 。

(c) 初始正定矩陣 ${{\rm{H}}_0}$ 取定後， ${{\rm{H}}_{k + 1}}$ 應該由 ${{\rm{H}}_k}$ 遞推給出，即 ${{\rm{H}}_{k + 1}} = {{\rm{H}}_k} + {{\rm{E}}_k}$ ；其中 ${{\rm{E}}_k}$ 是修正矩陣， ${{\rm{H}}_{k + 1}} = {{\rm{H}}_k} + {{\rm{E}}_k}$ 是修正公式。

常用而且有效的修正公式是BFGS公式，如下

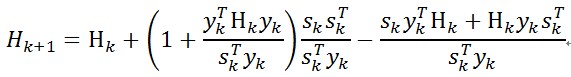
下面給出BFGS公式下的擬牛頓法

在上述步驟中，初始正定矩陣 ${{\rm{H}}_0}$ 通常取為單位矩陣，即 ${{\rm{H}}_0} = {\rm{I}}$ 。這樣，擬牛頓法的第一次迭代相當於一個最速下降迭代。

1.3.3.2優缺點

與牛頓法相比，有兩個優點：

(a) 僅需一階導數

(b) 校正保持正定性，因而下降性質成立

(c) 無需計算逆矩陣，但具有超線性收斂速度

(d) 每次迭代僅需要次乘法計算

缺點是初始點距離最優解遠時速度還是慢。

解決方法是，迭代前期用最速下降法進行迭代，得到一定解以後用擬牛頓法迭代。

最優化之無約束優化

1.1問題定義

1.1.1優化問題定義

1.1.2最優化方法定義

1.1.3收斂速度簡介

1.2步長確定

1.2.1一維搜尋

1.2.1.1確定搜尋區間

1.2.1.2搜尋求解

1.2.2不精確一維搜尋方法

1.3方向確定

1.3.1最速下降法

1.3.1.1演算法步驟

1.3.1.2缺點

1.3.2牛頓法

1.3.2.1演算法思想和步驟

1.3.2.2缺點

1.3.3擬牛頓法

1.3.3.1演算法思想和步驟

1.3.3.2優缺點

1.1問題定義

1.1.1優化問題定義

1.1.2最優化方法定義

1.1.3收斂速度簡介

1.2步長確定

1.2.1一維搜尋

1.2.1.1確定搜尋區間

1.2.1.2搜尋求解

1.2.2不精確一維搜尋方法

1.3方向確定

1.3.1最速下降法

1.3.1.1演算法步驟

1.3.1.2缺點

1.3.2牛頓法

1.3.2.1演算法思想和步驟

1.3.2.2缺點

1.3.3擬牛頓法

1.3.3.1演算法思想和步驟

1.3.3.2優缺點

相關文章