【Codeforces Round 362 (Div 2)E】【公式推導+快速冪+費馬小定理】PLEASE a[i]=(1-a[i-1])除2下n次項 n為連乘數

As we all know Barney's job is "PLEASE" and he has not much to do at work. That's why he started playing "cups and key". In this game there are three identical cups arranged in a line from left to right. Initially key to Barney's heart is under the middle cup.

Then at one turn Barney swaps the cup in the middle with any of other two cups randomly (he choses each with equal probability), so the chosen cup becomes the middle one. Game lasts n turns and Barney independently choses a cup to swap with the middle one within each turn, and the key always remains in the cup it was at the start.

After n-th turn Barney asks a girl to guess which cup contains the key. The girl points to the middle one but Barney was distracted while making turns and doesn't know if the key is under the middle cup. That's why he asked you to tell him the probability that girl guessed right.

Number n of game turns can be extremely large, that's why Barney did not give it to you. Instead he gave you an array a₁, a₂, ..., a_ksuch that

in other words, n is multiplication of all elements of the given array.

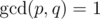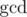Because of precision difficulties, Barney asked you to tell him the answer as an irreducible fraction. In other words you need to find it as a fraction p / q such that , where  is the greatest common divisor. Since p and q can be extremely large, you only need to find the remainders of dividing each of them by 10⁹ + 7.

Please note that we want 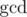 of p and q to be 1, not 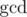 of their remainders after dividing by 10⁹ + 7.

1
2

1/2

3
1 1 1

0/1

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 0, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n;
const int G = 2;//矩陣大小
struct MX
{
	int v[G][G];
	void O() { MS(v, 0); }
	void E() { MS(v, 0); for (int i = 0; i<G; i++)v[i][i] = 1; }
	MX operator * (const MX &b) const
	{
		MX c; c.O();
		for (int i = 0; i<G; i++)
		{
			for (int j = 0; j<G; j++)
			{
				for (int k = 0; k<G; k++)
				{
					c.v[i][j] = (c.v[i][j] + (LL)v[i][k] * b.v[k][j]) % Z;
				}
			}
		}
		return c;
	}
	MX operator + (const MX &b) const
	{
		MX c; c.O();
		for (int i = 0; i<G; i++)
		{
			for (int j = 0; j<G; j++)
			{
				c.v[i][j] = (v[i][j] + b.v[i][j]) % Z;
			}
		}
		return c;
	}
	MX operator ^ (LL p) const
	{
		MX y; y.E();
		MX x; MC(x.v, v);
		while (p)
		{
			if (p & 1)y = y*x;
			x = x*x;
			p >>= 1;
		}
		return y;
	}
}a,b,c;
void tryit(int p)
{
	b.O();
	b.v[0][0] = 4;
	b.v[1][0] = b.v[1][1] = 1;
	a.O();
	a.v[0][0] = 0;
	a.v[0][1] = 1;
	c = a*(b ^ (p / 2));
	int ans = c.v[0][0];
	if (p & 1)ans = (ans * 2 + 1) % Z;
	printf("%d", ans);
}
int mul(LL x, int p)
{
	LL y = 1;
	while (p)
	{
		if (p & 1)y = y*x%Z;
		x = x*x%Z;
		p >>= 1;
	}
	return y;
}
void fast(int tim)
{
	int top = mul(2, tim);
	if (tim & 1) { top += 1; if (top >= Z)top -= Z; }
	else { top -= 1; if (top < 0)top += Z; }
	top = (LL)top * mul(3, Z - 2) % Z;
	printf("%d", top);
}
int main()
{
	while (~scanf("%d", &n))
	{
		LL tim = 1;
		for (int i = 1; i <= n; ++i)
		{
			LL x;
			scanf("%lld", &x); x %= (Z - 1);
			tim *= x;
			tim %= (Z - 1);
		}
		tim = (tim + Z - 2) % (Z - 1);
		//tryit(tim);//矩陣快速冪做法
		fast(tim);//快速冪做法
		printf("/");
		printf("%d\n", mul(2, tim));
	}
	return 0;
}
/*
【題意】
>.< 不說原題意了
稍微轉化一下，問題變為——
a[0]=1;
a[i]=(1-a[i-1])/2
用分數的形式輸出a[n]（分子分母先約分，再%(Z=1e9+7)）
其中n以若干個數乘積的形式給出

【型別】
費馬小定理 + （矩陣快速冪 or 快速冪）

【分析】
首先n這麼大，我們要怎麼辦？
可以用nlogn的快速冪做迭代，
也可以通過費馬小定理化簡。
所謂費馬小定理，是說，（x^(Z-1)）%Z==1（Z為素數），即對於x的冪而言，每Z-1個就完成一次迴圈。
於是，我們對冪做%(Z-1)的連乘，得到的tim用於之後的計算。

之後要如何算你？
a[i]=(1-a[i-1])/2
我們找規律，是這樣子的——
1 0 1/2 1/4 3/8 5/16
我們發現，分母一直*=2，分子是以（*2+1），（*2-1）的方式錯交替性。
分母為2的冪次，分子為奇數不含2，於是分母與分子其實並沒有約分的必要。

分母的話，快速冪可以搞定
分子的話，我們可以通過矩陣快速冪搞定
把（*2+1）和（*2-1）合併為（*4+1）

不過我的做法有點粗暴，這道題可以直接用快速冪搞定。
先要推公式——
a[i]=(1-a[i-1])/2
得到2a[i] = (1-a[i-1])
得到2(a[i]-1/3)=-(a[i-1]-1/3)
所以(a[i]-1/3)是一個以(a[0]-1/3)為首項，以(-1/2)為公比的等比數列。

於是我們求出——
(a[n]-1/3)=(2/3)*(-1/2)^n
這樣，如果n為偶數，那麼結果為(1+2^(n-1))/3*2^(n-1)
如果n為奇數，那麼結果為(-1+2^(n-1))/3*2^(n-1)

於是我們可以快速求出解來。

【時間複雜度&&優化】
O(n)

*/