【Codeforces Round 362 (Div 2)C】【STL-map 最近公共祖先思想】Lorenzo Von Matterhorn 數域二叉樹的路徑權值變更查詢

Barney lives in NYC. NYC has infinite number of intersections numbered with positive integers starting from 1. There exists a bidirectional road between intersections i and 2i and another road between i and 2i + 1 for every positive integer i. You can clearly see that there exists a unique shortest path between any two intersections.

Initially anyone can pass any road for free. But since SlapsGiving is ahead of us, there will qconsecutive events happen soon. There are two types of events:

1. Government makes a new rule. A rule can be denoted by integers v, u and w. As the result of this action, the passing fee of all roads on the shortest path from u to v increases by w dollars.

2. Barney starts moving from some intersection v and goes to intersection u where there's a girl he wants to cuddle (using his fake name Lorenzo Von Matterhorn). He always uses the shortest path (visiting minimum number of intersections or roads) between two intersections.

Government needs your calculations. For each time Barney goes to cuddle a girl, you need to tell the government how much money he should pay (sum of passing fee of all roads he passes).

7
1 3 4 30
1 4 1 2
1 3 6 8
2 4 3
1 6 1 40
2 3 7
2 2 4

94
0
32

Note

In the example testcase:

Here are the intersections used:

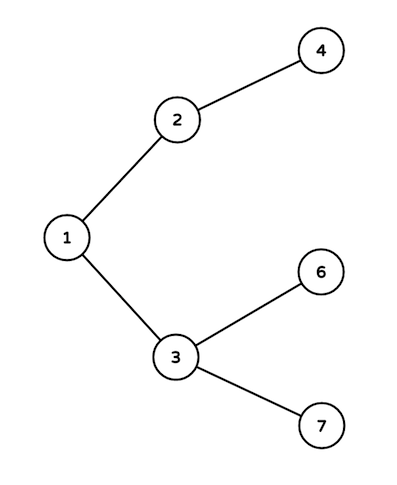
1. Intersections on the path are 3, 1, 2 and 4.
2. Intersections on the path are 4, 2 and 1.
3. Intersections on the path are only 3 and 6.
4. Intersections on the path are 4, 2, 1 and 3. Passing fee of roads on the path are 32, 32and 30 in order. So answer equals to 32 + 32 + 30 = 94.
5. Intersections on the path are 6, 3 and 1.
6. Intersections on the path are 3 and 7. Passing fee of the road between them is 0.
7. Intersections on the path are 2 and 4. Passing fee of the road between them is 32(increased by 30 in the first event and by 2 in the second).

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 0, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n;
map<LL, LL>mop;
void add(LL x, LL y, LL z)
{
	while (x != y)
	{
		if (y > x)swap(x, y);
		mop[x] += z;
		x >>= 1;
	}
}
LL check(LL x, LL y)
{
	LL sum = 0;
	while (x != y)
	{
		if (y > x)swap(x, y);
		if (mop.count(x))sum += mop[x];
		x >>= 1;
	}
	return sum;
}
int main()
{
	while (~scanf("%d", &n))
	{
		mop.clear();
		int op;
		LL x, y, z;
		for (int i = 1; i <= n; ++i)
		{
			scanf("%d", &op);
			if (op == 1)
			{
				scanf("%lld%lld%lld", &x, &y, &z);
				add(x, y, z);
			}
			else
			{
				scanf("%lld%lld", &x, &y);
				printf("%lld\n", check(x, y));
			}
		}
	}
	return 0;
}
/*
【題意】
對於正整數域上的二叉樹，x的左兒子為2x，右兒子為2x+1
有q（1000）次操作。
對於每次操作，有兩種型別：
1 x,y,z 我們增加從x到y路徑上每條邊的權值為z
2 x y 詢問從x到y的路徑邊權

【型別】
STL - map 最近公共祖先思想

【分析】
雖然數域範圍很大，但是運算元很小，我們可以用一個map
mop[x]表示x到其父節點的路徑上的權值累計量。
然後我們就可以O(lognlogn)的複雜度維護每次詢問啊

【時間複雜度&&優化】
O(qlognlogn)

*/