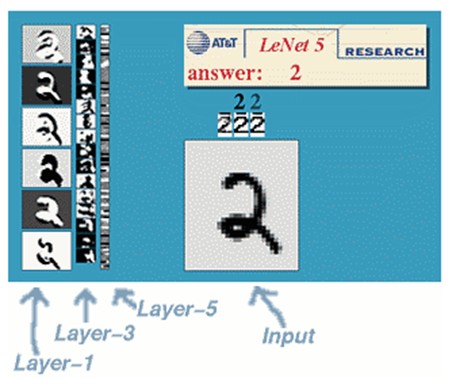
文字識別系統LeNet-5
在經典的模式識別中,一般是事先提取特徵。提取諸多特徵後,要對特徵進行相關性分析,找到最能代表字元的特徵,去掉對分類無關和自相關的特徵。然而,這些特徵的提取太過依賴人的經驗和主觀意識,提取到的特徵的不同對分類效能影響很大,甚至提取的特徵的順序也會影響最後的分類效能。同時,影像預處理的好壞也會影響到提取的特徵。那麼,如何把特徵提取這一過程作為一個自適應、自學習的過程,通過機器學習找到分類效能最優的特徵呢?
卷積神經元每一個隱層的單元提取影像區域性特徵,將其對映成一個平面,特徵對映函式採用sigmoid函式作為卷積神經網路的啟用函式,使得特徵對映具有位移不變性。每個神經元與前一層的區域性感受野相連。注意前面我們說了,不是區域性連線的神經元權值相同,而是同一平面層的神經元權值相同,有相同程度的位移、旋轉不變性。每個特徵提取後都緊跟著一個用來求區域性平均與二次提取的亞取樣層。這種特有的兩次提取結構使得網路對輸入樣本有較高的畸變容忍能力。也就是說,卷積神經網路通過區域性感受野、共享權值和亞取樣來保證影像對位移、縮放、扭曲的魯棒性。
文字識別系統LeNet-5
一種典型的用來識別數字的卷積網路是LeNet-5。當年美國大部分銀行就是用它來識別支票上面的手寫數字的。能夠達到這種商用的地步,它的準確性可想而知。畢竟目前學術界和工業界的結合是最受爭議的。
那下面我們也用這個例子來說明下:
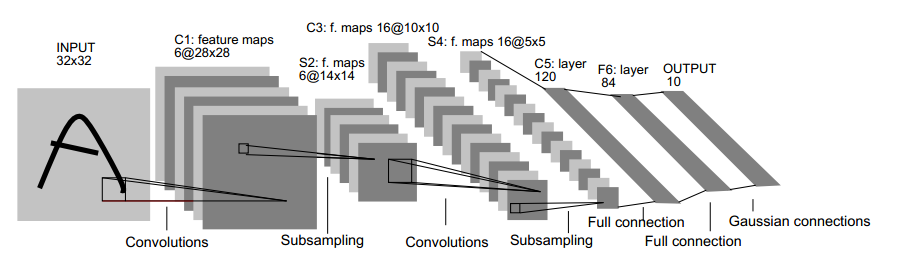
LeNet-5共有7層,不包含輸入,每層都包含可訓練引數(連線權重)。輸入影像為32*32大小。這要比Mnist資料庫(一個公認的手寫資料庫)中最大的字母還大。這樣做的原因是希望潛在的明顯特徵如筆畫斷點或交點能夠出現在最高層特徵監測子感受野的中心。
首先,簡要解釋上面這個用於文字識別的LeNet-5深層卷積網路:
1.輸入影像是32*32的大小,區域性滑動窗的大小是5*5的,由於不考慮對影像的邊界進行擴充,則滑動窗將有28*28個不同的位置,也就是C1層的大小是28*28。這裡設有6個不同的C1層,每一個C1層內的權值是相同的。
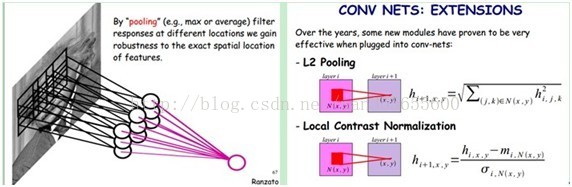
2.S2層是一個下采樣層。簡單地說,由4個點下采樣為1個點,也就是4個數的加權平均。但在LeNet-5系統,下采樣層比較度雜,因為這4個加權係數也需要學習得到,這顯然增加了模型的複雜度。在史丹佛關於深度學習的教程中,這個過程叫做Pool。
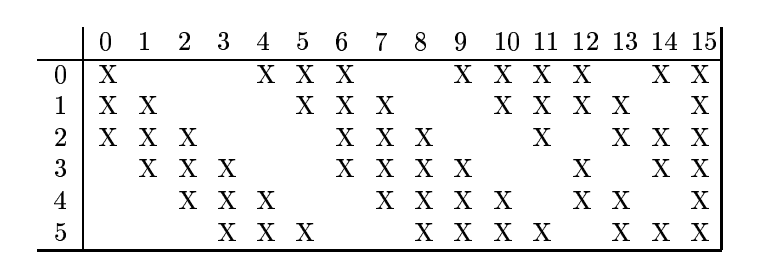
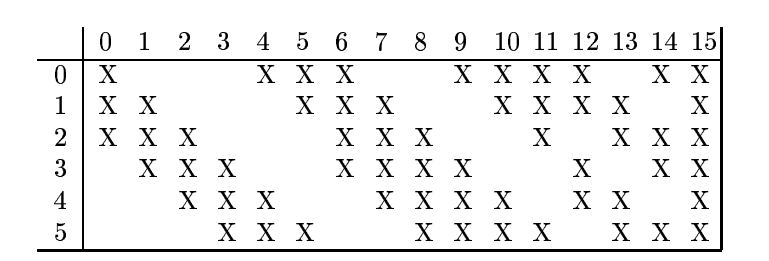
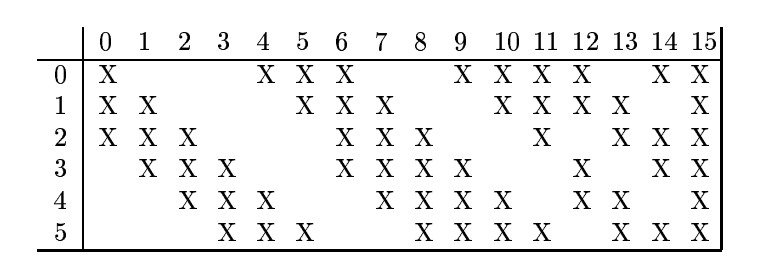
3.根據對前面C1層同樣的理解,我們很容易得到C3層的大小為10*10,只不過,C3層變成了16個10*10網路。試想一下,如果S2層只有1個平面,那麼由S2層得到C3層就和由輸入層得到C1層是完全一樣的。但是,S2層有多層,那麼,我們只需要按照一定的順序組合這些層就可以了。具體的組合機制,在LeNet-5系統中給出了下面的表格:
簡單的說,例如對於C3層第0張特徵圖,其每一個節點與S2層的第0張特徵圖,第1張特徵圖,第2張特徵圖,總共3個5*5節點相連線。後面以此類推。C3層每一張特徵對映圖的權值是相同的。
4.S4層是在C3層基礎上取樣,前面已述。在後面的層由於每一層節點個數比較少,都是全連線層,這個比較簡單,不再贅述。
涉及問題:
1、每個圖如何卷積:
(1)一個圖如何變成幾個?
(2)卷積核如何選擇?
2、節點之間如何連線?
3、S2-C3如何進行分配?
4、16-120全連線如何連線?
5、最後output輸出什麼形式?
提前對各個層進行解釋,以方便後面給出答案:
我們先要明確一點:每個層有多個Feature Map,每個Feature Map通過一種卷積濾波器提取輸入的一種特徵,然後每個Feature Map有多個神經元。
(1)C1層是一個卷積層(為什麼是卷積?卷積運算是一個重要的特點就是,通過卷積運算,可以使原訊號特徵增強,並且降低噪音),由6個特徵圖Feature Map構成。特徵圖中每個神經元與輸入中5*5的鄰域相連。特徵圖的大小為28*28,這樣能防止輸入的連線掉到邊界之外(是為了BP反饋時的計算,不致梯度損失,個人見解)。C1層有156個可訓練引數(每個訓練器5*5=25個unit引數和1個bias引數,一共6個濾波器,共(5*5+1)*6=156個引數),共156*(28*28)=122304個連線。
(2)S2層是一個下采樣層(為什麼是下采樣?利用影像區域性相關性的原理,對影像進行子抽樣,可以減少資料處理量同時保留有用資訊),有6個14*14的特徵圖。特徵圖中的每個單元與C1中相對應特徵圖的2*2鄰域相連線。S2層對應C1層每4個單元輸入相加,乘以一個可訓練引數,再加上一個可訓練偏置。結果通過Sigmoid函式計算。可訓練係數和偏置控制著Sigmoid函式的非線性程度。如果係數比較小,那麼運算近似於線性運算,亞取樣相當於模糊影像。如果係數比較大,根據偏置的大小亞取樣可以被看成是有噪聲的“或”運算或者有噪聲的“與”運算。每個單元的2*2感受野並不重疊,因此S2中每個特徵圖的大小是C1中特徵圖大小的1/4(行和列各1/2)。S2層有12個可訓練引數和588個連線。
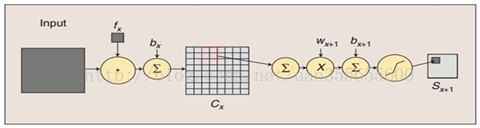
圖:卷積和子取樣過程:卷積過程包括:用一個可訓練的濾波器fx去卷積一個輸入的影像(第一階段是輸入的影像,後面的階段就是卷積特徵map了),然後加一個偏置bx,得到卷積層Cx。子取樣過程包括:每鄰域四個畫素求和變為一個畫素,然後通過標量Wx+1加權,再增加偏置bx+1,然後通過一個sigmoid啟用函式,產生一個大概縮小四倍的特徵對映圖Sx+1。
所以從一個平面到下一個平面的對映可以看作是作卷積運算,S-層可看作是模糊濾波器,起到二次特徵提取的作用。隱層與隱層之間空間解析度遞減,而每層所含的平面數遞增,這樣可用於監測更多的特徵資訊。
(3)C3層也是一個卷積層,它同樣通過5*5的卷積核去卷積層S2,然後得到的特徵map就只有10*10個神經元,但是它有16種不同的卷積核,所以就存在16個特徵map了。這裡需要注意一點是:C3中的每個特徵map是連線到S2中的所有6個或者幾個特徵map的,表示本層的特徵map是上一層提取到的特徵map的不同組合(這個做法也並不是唯一的)。(看到沒有,這裡是組合,就像之前聊到的人的視覺系統一樣,底層的結構構成上層更抽象的結構,例如邊緣構成形狀或者目標的部分)。
剛才說C3中每個特徵圖由S2層中所有6個或者幾個特徵map組合而成。為什麼不把S2中的每個特徵圖連線到每個C3的特徵圖呢?原因有2點。第一,不完全的連線機制將連線的數量保持在合理的範圍內。第二,也是最重要的,其破壞了網路的對稱性。由於不同的特徵圖有不同的輸入,所以迫使它們抽取不同的特徵(希望是互補的)。
例如,存在一個方式是:C3的前6個特徵圖以S2中3個相鄰的特徵圖子集為輸入;接下來6個特徵圖以S2中4個相鄰特徵圖子集為輸入;然後3個以不相鄰的4個特徵子集為輸入;最後一個將S2中所有特徵圖作為輸入,這樣C3層有1516個可訓練引數和151600個連線。
(4)S4層是一個下采樣層,由16個5*5大小的特徵圖構成。特徵圖中的每個單元與C3層中相應特徵圖的2*2鄰域相連線,跟C1和S2之間的連線一樣。S4層有32個可訓練引數(每個特徵圖1個權重因子和1個偏置)和2000個連線。
(5)C5層是一個卷積層,有120個特徵圖。每個單元與S4層的全部16個單元的5*5鄰域相連。由於S4層特徵圖的大小也為5*5(同濾波器一樣),故C5特徵圖的大小為1*1,這構成了S4和C5之間的全連線。之所以仍將C5標示為卷積層而非全連線層,是因為如果LeNet-5的輸入變大,而其他的保持不變,那麼此時特徵圖的維數就會比1*1大。C5層有49920個可訓練連線。
(6)F6層有84個單元(之所以選這個數字的原因來自於輸出層的設計),與C5層全相連。有10164個可訓練引數。如同經典神經網路,F6層計算輸入向量和權重向量之間的點積,再加上一個偏置。然後將其傳遞給Sigmoid函式產生單元的一個狀態。
(7)最後,輸出層由歐式徑向基函式(Euclidean Radial Basis Function)單元組成,每類一個單元,每個有84個輸入。換句話說,每個輸入RBF單元計算輸入向量和引數向量之間的歐式距離。輸入離引數向量越遠,RBF輸出的越大。一個RBF輸出可以被理解為衡量輸入模式和與RBF相關聯類的一個模型的匹配程度的懲罰項。用概率術語來說,RBF輸出可以被理解為F6層配置空間的高斯分佈的負log-looklihood。給定一個輸入模式,損失函式應能使得F6的配置與RBF引數向量(即模式的期望分類)足夠接近。這些單元的引數是人工選取並保持固定的(至少初始時如此)。這些引數向量的成分被設為-1或1。雖然這些引數可以以-1和1等概率的方式任選,或者構成一個糾錯碼,但是被設計成一個相應字元類的7*12大小(即84)的格式化圖片。這種表示對識別單獨的數字不是很有用,但是對識別可列印ASCII集中的字串很有用。
用這種分佈編碼而非更常用的1 of N編碼用於產生輸出的另一個原因是,當類別比較大時,非分佈編碼的效果比較差。原因是大多數時間非分佈編碼的輸出必須為0,這使得用sigmoid單元很難實現。另一個原因是分類器不僅用於識別字母,也用與拒絕非子母。使用分佈編碼的RBF更適合該目標。因為與sigmoid不同,它們在輸入空間的較好限制區域內興奮,而非典型模式更容易落到外邊。
RBF引數向量起著F6層目標向量的角色。需要指出這些向量的成分是+1或-1,這正好是F6 sigmoid的範圍內,因此可以防止sigmoid函式飽和。實際上,+1和-1是sigmoid函式的最大彎曲的點處。這使得F6單元執行在最大非線性範圍內。必須避免sigmoid函式的飽和,因為這將會導致損失函式較慢的收斂和病態問題。
問題講解:
第一個問題:
(1)輸入-C1
用6個5*5大小的patch(即權值,訓練的到,隨機初始化,在訓練過程中調節)對32*32圖片進行卷積,得到6個特徵圖。
(2)S2-C3
C3那16張10*10大小的特徵圖是怎麼來的?
將S2的特徵圖用1個輸入層為150(=5*5*6,不是5*5)個節點的網路進行convolution。
該第3號特徵圖的值(假設為H3)是怎麼得到的?
首先我們把網路150-16(以後這樣表示,表示輸入層節點為150,隱含層節點為16)中輸入的150個節點分成6個部分,每個部分為連續的25個節點。取出倒數第3個部分的節點(為25個),且同時是與隱含層16個節點中的第4(因為對應的是3號,從0開始計數)個相連的那25個值,reshape為5*5大小,用這個5*5大小的特徵patch去convolution S2網路中的倒數第3個特徵圖,假設得到的結果特徵為h1。
同理,取出網路150-16中輸入的倒數第2個部分的節點(為25個),且同時是與隱含層16個節點中的第5個相連的那25個值,reshape為5*5大小,用這個5*5大小的特徵patch去convolution S2網路中的倒數第2個特徵圖,假設得到的結果特徵圖為h2。
最後,取出網路150-16中輸入的最後1個部分的節點(為25個),且同時是與隱含層16個節點中的第5個相連的那25個值,reshape為5*5大小,用這個5*5大小的特徵patch去convolution S2網路中的最後1個特徵圖,假設得到的結果特徵圖為h3。
最後將h1,h2,h3這3個矩陣相加得到新矩陣h,並且對h中每個元素加上一個偏移量b,且通過sigmoid的激發函式,即可得到我們要的特徵圖H3了。
第二個問題:
上圖S2中為什麼是150個節點?(涉及到權值共享和引數減少)
CNN一個牛逼的地方就在於通過感受野和權值共享減少了神經網路需要訓練的引數的個數。
下圖左:如果我們有1000x1000畫素的影像,有1百萬個隱層神經元,那麼他們全連線的話(每個隱層神經元都連線影像的每一個畫素點),就有1000x1000x1000000=10^12個連線,也就是10^12個權值引數。然而影像的空間聯絡是區域性的,就像人是通過一個區域性的感受野去感受外界影像一樣,每一個神經元都不需要對全域性影像做感受,每個神經元只感受區域性的影像區域,然後在更高層,將這些感受不同區域性的神經元綜合起來就可以得到全域性的資訊了。這樣,我們就可以減少連線的數目,也就是減少神經網路需要訓練的權值引數的個數了。如下圖右:假如區域性感受野是10x10,隱層每個感受野只需要和這10x10的區域性影像相連線,所以1百萬個隱層神經元就只有一億個連線,即10^8個引數。比原來減少了四個0(數量級),這樣訓練起來就沒那麼費力了,但還是感覺很多的啊,那還有啥辦法沒?
我們知道,隱含層的每一個神經元都連線10x10個影像區域,也就是說每一個神經元存在10x10=100個連線權值引數。那如果我們每個神經元這100個引數是相同的呢?也就是說每個神經元用的是同一個卷積核去卷積影像。這樣我們就只有多少個引數??只有100個引數啊!!!親!不管你隱層的神經元個數有多少,兩層間的連線我只有100個引數啊!親!這就是權值共享啊!親!這就是卷積神經網路的主打賣點啊!親!(有點煩了,呵呵)也許你會問,這樣做靠譜嗎?為什麼可行呢?這個……共同學習。
好了,你就會想,這樣提取特徵也忒不靠譜吧,這樣你只提取了一種特徵啊?對了,真聰明,我們需要提取多種特徵對不?假如一種濾波器,也就是一種卷積核就是提出影像的一種特徵,例如某個方向的邊緣。那麼我們需要提取不同的特徵,怎麼辦,加多幾種濾波器不就行了嗎?對了。所以假設我們加到100種濾波器,每種濾波器的引數不一樣,表示它提出輸入影像的不同特徵,例如不同的邊緣。這樣每種濾波器去卷積影像就得到對影像的不同特徵的放映,我們稱之為Feature Map。所以100種卷積核就有100個Feature Map。這100個Feature Map就組成了一層神經元。到這個時候明瞭了吧。我們這一層有多少個引數了?100種卷積核x每種卷積核共享100個引數=100x100=10K,也就是1萬個引數。才1萬個引數啊!親!(又來了,受不了了!)見下圖右:不同的顏色表達不同的濾波器。
嘿喲,遺漏一個問題了。剛才說隱層的引數個數和隱層的神經元個數無關,只和濾波器的大小和濾波器種類的多少有關。那麼隱層的神經元個數怎麼確定呢?它和原影像,也就是輸入的大小(神經元個數)、濾波器的大小和濾波器在影像中的滑動步長都有關!例如,我的影像是1000x1000畫素,而濾波器大小是10x10,假設濾波器沒有重疊,也就是步長為10,這樣隱層的神經元個數就是(1000x1000 )/ (10x10)=100x100個神經元了,假設步長是8,也就是卷積核會重疊兩個畫素,那麼……我就不算了,思想懂了就好。注意了,這只是一種濾波器,也就是一個Feature Map的神經元個數哦,如果100個Feature Map就是100倍了。由此可見,影像越大,神經元個數和需要訓練的權值引數個數的貧富差距就越大。
所以這裡可以知道剛剛14*14的影像計算它的節點,按步長為3計算,則一幅圖可得5*5個神經元個數,乘以6得到150個神經元個數。
需要注意的一點是,上面的討論都沒有考慮每個神經元的偏置部分。所以權值個數需要加1 。這個也是同一種濾波器共享的。
總之,卷積網路的核心思想是將:區域性感受野、權值共享(或者權值複製)以及時間或空間亞取樣這三種結構思想結合起來獲得了某種程度的位移、尺度、形變不變性。
第三個問題:
如果C1層減少為4個特徵圖,同樣的S2也減少為4個特徵圖,與之對應的C3和S4減少為11個特徵圖,則C3和S2連線情況如圖:
第四個問題:
全連線:
C5對C4層進行卷積操作,採用全連線方式,即每個C5中的卷積核均在S4所有16個特徵圖上進行卷積操作。
第五個問題:
採用one-of-c的方式,在輸出結果的1*10的向量中最大分量對應位置極為網路輸出的分類結果。對於訓練集的標籤也採用同樣的方式編碼,例如1000000000,則表明是數字0的分類。
簡化的LeNet-5系統
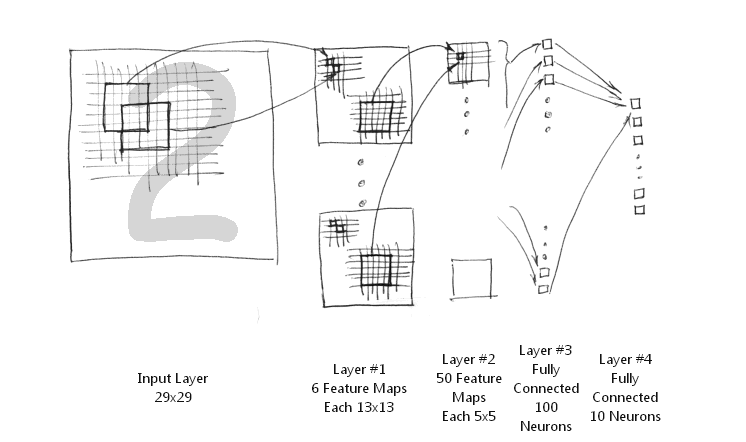
簡化的LeNet-5系統把下采樣層和卷積層結合起來,避免了下采樣層過多的引數學習過程,同樣保留了對影像位移,扭曲的魯棒性。其網路結構圖如下所示:
簡化的LeNet-5系統包括輸入層的話,只有5層結構,而原始LeNet-5結構不包含輸入層就已經是7層網路結構了。它實現下采樣非常簡單,直接取其第一個位置節點上的值可以了。
1、 輸入層。MNIST手寫數字影像的大小是28x28的,這裡通過補零擴充套件為29x29的大小。這樣輸入層神經節點個數為29x29等於841個。
2、第一層。由6張不同的特徵對映圖組成。每一張特徵圖的大小是13x13. 注意,由於卷積窗大小為5x5,加上下采樣過程,易得其大小為13x13. 所以, 第二層共有6x13x13等於1014個神經元節點。每一張特徵圖加上偏置共有5x5+1等於26個權值需要訓練,總共有6x26等於156個不同的權值。即總共有1014x156等於26364條連線線。
3、 第二層。由50張不同的特徵對映圖組成。每一張特徵圖的大小是5x5. 注意,由於卷積窗大小為5x5,加上下采樣過程,易得其大小為5x5. 由於上一 層是由多個特徵對映圖組成,那麼,如何組合這些特徵形成下一層特徵對映圖的節點呢?簡化的LeNet-5系統採用全部所有上層特徵圖的組合。也就是原始LeNet-5 特徵對映組合圖的最後一列的組合方式。因此,總共有5x5x50等於1250 個神經元節點,有(5x5+1)x6x50等於7800 個權值,總共有1250x26等於32500條連線線。
4、第三層。 這一層是一個一維線性排布的網路節點,與前一層是全連線的網路,其節點個數設為為100,故而總共有100x(1250+1)等於125100個不同的權值,同時,也有相同數目的連線線。
5、第四層。這一層是網路的輸出層,如果要識別0-9數字的話,就是10個節點。該層與前一層是全連線的,故而,總共有10x(100+1)等於1010個權值,有相同數目的連線線。
相關文章
- 中安OCR文字識別系統
- 通用文字識別API-通用文字識別介面可以識別哪些場景文字API
- Node.js文字識別介面、文字錄入、線上免費文字識別介面Node.js
- 裝置漏油檢測識別系統 漏油自動識別系統
- 車牌識別系統
- 河道水位識別系統
- 文字識別(三)--文字定位與切割
- 圖片裁剪-文字識別-文字新增
- 文字識別(六)--不定長文字識別CRNN演算法詳解RNN演算法
- 車牌識別系統、車牌識別整合、車牌識別介面
- ocr文字識別軟體怎麼識別手機上的照片文字?
- OCR文字識別系統助力快遞行業提高快遞分揀效率行業
- 文字識別(二)--字元識別技術總覽字元
- ocr文字識別技術
- Java識別作業系統Java作業系統
- aix 系統識別符號AI符號
- 安全通道堵塞識別系統
- 5 款不錯的開源語音識別/語音文字轉換系統
- 有道自然語言翻譯和文字識別OCR(圖片文字識別)介面呼叫
- 如何免費識別圖片文字?圖片文字識別軟體怎麼用
- 人臉識別智慧考勤系統開發_人臉識別考勤管理系統開發
- OCR技術-文字影像識別
- 分享:識別圖片文字方法
- Crystal 實現文字識別程式
- 系統無法識別SATA硬碟硬碟
- 渣土車識別檢測系統
- 人員行為識別系統
- 出料口堵塞識別系統
- 智慧工地煙火識別系統
- 工人規範操作識別系統
- 人員著裝識別系統
- 防溺水預警識別系統
- 行人闖紅燈識別預警系統
- 煙塵監測識別系統
- 佩戴安全帽識別系統
- 河道水位監測識別系統
- 工地安全著裝識別系統
- 安全通道異常識別系統