深度解析CNN

1、概述

卷積神經網路是一種特殊的深層的神經網路模型，它的特殊性體現在兩個方面，一方面它的神經元間的連線是非全連線的，另一方面同一層中某些神經元之間的連線的權重是共享的（即相同的）。它的非全連線和權值共享的網路結構使之更類似於生物神經網路，降低了網路模型的複雜度（對於很難學習的深層結構來說，這是非常重要的），減少了權值的數量。

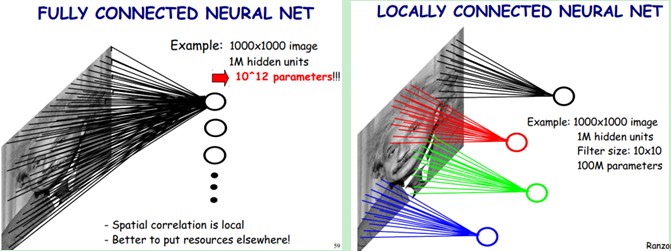
回想一下BP神經網路。BP網路每一層節點是一個線性的一維排列狀態，層與層的網路節點之間是全連線的。這樣設想一下，如果BP網路中層與層之間的節點連線不再是全連線，而是區域性連線的，這樣，就是一種最簡單的一維卷積網路。如果把上述這個思路擴充套件到二維，這就是我們在大多數參考資料上看到的卷積神經網路。具體參看下圖：

上圖左：全連線網路。如果我們有1000*1000畫素的影像，有1百萬個隱層神經元，每個隱層神經元都連線影像的每一個畫素點，就有1000*1000*1000000=10^12個連線，也就是10^12個權值引數。

上圖右：區域性連線網路，每一個節點與上層節點同位置附近10*10的視窗相連線，則1000000個隱層神經元就只有1000000*100=10^8個引數。其權值連線個數比原來減少了4個數量級。

根據BP網路訊號前向傳遞過程，我們可以很容易計算網路節點的輸出。例如，對於上圖中被標註為紅色節點的淨輸入，就等於所有與紅線相連線的上一層神經元節點值與紅色線表示的權值之積的累加。這樣的計算過程，很多書上稱其為卷積。

事實上，對於數字濾波而言，其濾波器的係數通常是對稱的，否則，卷積計算需要先反向對摺，然後進行乘累加的計算。上述神經網路權值滿足對稱嗎？我想答案是否定的。所以，上述稱其為卷積運算，顯然是有失偏頗的。但這並不重要，僅僅是一個名詞稱謂而已。只是，搞訊號處理的人，在初次接觸卷積神經網路的時候，帶來了一些理解上的誤區。

卷積神經網路另外一個特性是權值共享（即同一個特徵對映上的神經元使用相同的卷積核）。例如，就上面右邊那幅圖來說，權值共享，不是說所有的紅色線標註的連線值相同。這一點，初學者容易產生誤解。

上面描述的只是單層神經網路，前AT&TShannon Lab的Yann LeCun等人據此提出了基於卷積神經網路的一個文字識別系統(LeNet-5)。該系統90年代被用於銀行手寫數字的識別。

2、CNN結構

卷積網路是為識別二維形狀而特殊設計的一個多層感知器，這種網路結構對平移、比例縮放、傾斜或者其他形式的變形具有高度不變性。這些良好的效能是網路在有監督方式下學會的，網路的結構主要有稀疏連線和權值共享兩個特點，包括如下形式的約束：

• 特徵提取。每一個神經元從上一層的區域性接受域得到突觸輸入，因而迫使它提取區域性特徵。一旦一個特徵被提取出來，只要它相對於其他特徵的位置被近似地保留下來，它的精確位置就變得沒有那麼重要了。
• 特徵對映。網路的每一個計算層都是由多個特徵對映組成的，每個特徵對映都是平面形式的。平面中單獨的神經元在約束下共享相同的突觸權值集，這種結構形式具有如下的有益效果：a、平移不變性；b、自由引數數量的縮減（通過權值共享實現）。
• 子抽樣。每個卷積層後面跟著一個實現區域性平均和子抽樣的計算層，由此特徵對映的解析度降低。這種操作具有使特徵對映的輸出對平移和其他形式變形的敏感度下降的作用。

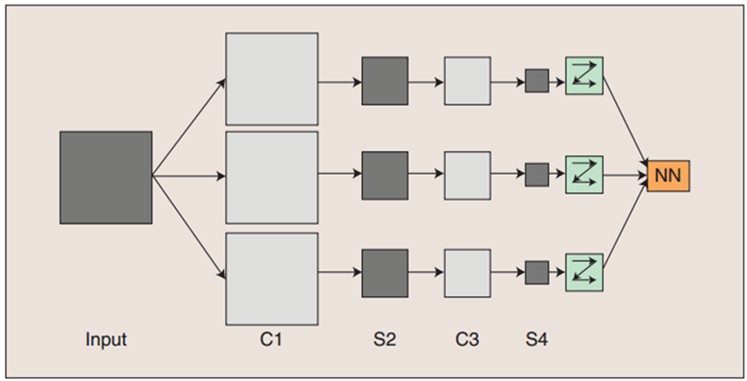
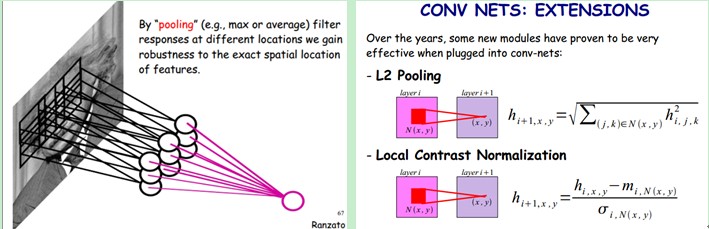
卷積神經網路的概念示範

輸入影像通過和三個可訓練的濾波器（卷積核）和可加偏執進行卷積，卷積後在C1層產生三個特徵對映圖，然後特徵對映圖中每組的四個畫素再進行求和，加權值，加配置，通過一個Sigmoid函式得到三個S2層的特徵對映圖。這些對映圖再通過濾波得到C3層。這個層級結構再和S2一樣產生S4。最終，這些畫素值被光柵化，並連線成一個向量輸入到傳統的神經網路，得到輸出。

一般地，C層為特徵提取層，每個神經元的輸入與前一層的區域性感受野相連，並提取該區域性的特徵，一旦該區域性特徵被提取後，它與其他特徵的位置關係也隨之確定下來；S層是特徵對映層，網路的每個計算層由多個特徵對映組成，每個特徵對映為一個平面，平面上所有神經元的權值相等。特徵對映結構採用影響函式核小的sigmoid函式作為卷積網路的啟用函式，使得特徵對映具有位移不變性。

此外，由於一個對映面上的神經元共享權值，因而減少了網路自由引數的個數，降低了網路引數選擇的複雜度。卷積神經網路中的每一個特徵提取層（C層）都緊跟著一個用來求區域性平均與二次提取的計算層（S層），這種特有的兩次特徵提取結構使網路在識別時對輸入樣本有較高的畸變容忍能力。

2.1稀疏連線（Sparse Connectivity）

卷積網路通過在相鄰兩層之間強制使用區域性連線模式來利用影像的空間區域性特性，在第m層的隱層單元只與第m-1層的輸入單元的區域性區域有連線，第m-1層的這些區域性區域被稱為空間連續的接受域。我們可以將這種結構描述如下：

設第m-1層為視網膜輸入層，第m層的接受域的寬度為3，也就是說該層的每個單元與且僅與輸入層的3個相鄰的神經元相連，第m層與第m+1層具有類似的連線規則，如下圖所示：

可以看到m+1層的神經元相對於第m層的接受域的寬度也為3，但相對於輸入層的接受域為5，這種結構將學習到的過濾器（對應於輸入訊號中被最大啟用的單元）限制在區域性空間模式（因為每個單元對它接受域外的variation不做反應）。從上圖可以看出，多個這樣的層堆疊起來後，會使得過濾器（不再是線性的）逐漸成為全域性的（也就是覆蓋到了更大的視覺區域）。例如上圖中第m+1層的神經元可以對寬度為5的輸入進行一個非線性的特徵編碼。

2.2權值共享（Shared Weights）

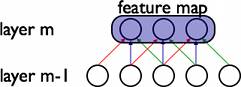
在卷積網路中，每個稀疏過濾器hi通過共享權值都會覆蓋整個可視域，這些共享權值的單元構成了一個特徵對映，如下圖所示：

在圖中，有3個隱層單元，它們屬於同一個特徵對映。同種顏色的連線權值是相同的，我們仍然可以使用梯度下降的方法來學習這些權值，只需要對原始演算法做一些小的改動，這裡共享權值的梯度是所有共享引數的梯度的總和。我們不禁會問為什麼要權重共享呢？一方面，重複單元能夠對特徵進行識別，而不考慮它在可視域中的位置。另一方面，權值共享使得我們能更有效的進行特徵抽取，因為它極大的減少了需要學習的自由變數的個數。通過控制模型的規模，卷積網路對視覺問題可以有很好的泛化能力。

舉例講解：

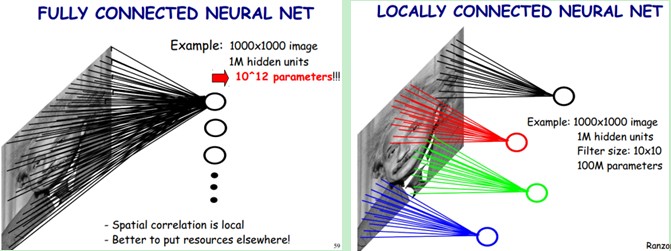
下圖左：如果我們有1000*1000畫素的影像，有1百萬個隱層神經元，每個隱層神經元都連線影像的每一個畫素點，就有1000*1000*1000000=10^12個連線，也就是10^12個權值引數。

然而影像的空間聯絡是區域性的，就像人是通過一個區域性的感受野去感受外界影像一樣，每一個神經元都不需要對全域性影像做感受，每個神經元只感受區域性的影像區域，然後在更高層，將這些感受不同區域性的神經元綜合起來就可以得到全域性的資訊了。這樣我們就可以減少連線的數目，也就是減少神經網路需要訓練的權值引數的個數了。

下圖右：假如區域性感受野是10*10，隱層每個感受野只需要和這10*10的區域性影像相連線，所以1百萬個隱層神經元就只要1億個連線，即10^8個引數。比原來減少了4個數量級，這樣訓練起來就沒那麼費力了，但還是感覺很多的啊。

我們知道，隱含層的每一個神經元都連線10*10個影像區域，也就是說，每一個神經元存在10*10=100個連線權值引數（卷積核）。如果每個神經元用的是同一個卷積核去卷積影像，這樣我們就只有100個引數啊，不管你隱層的神經元個數有多少，兩層間的連線只有100個引數！這就是權值共享。

但這樣只提取了一種特徵，假如一種濾波器，也就是一種卷積核，能夠提取出影像的一種特徵，例如某個方向的邊緣。那麼我們需要提取不同的特徵，就需要多使用幾種濾波器。所以假設使用100中濾波器，每種濾波器的引數不一樣，表示它提出輸入影像的不同特徵，例如不同的邊緣。這樣每種濾波器去卷積影像就得到對影像的不同特徵的對映，我們稱之為Feature Map。所以100種卷積核就有100個Feature Map。這100個Feature Map就組成了一層神經元。100種卷積核乘以卷積核共享100個引數=100*100=10K，也就是1萬個引數。見下圖右，不同顏色表達不同的濾波器：

剛才說隱層的引數個數和隱層的神經元個數無關，只和濾波器的大小和濾波器種類的多少有關。那麼隱層的神經元個數怎麼確定呢？它和原影像，也就是輸入的大小（神經元個數）、濾波器的大小和濾波器在影像中的滑動步長都有關。例如，我的影像是1000*1000畫素，而濾波器大小為10*10，假設濾波器沒有重疊，也就是步長為10，這樣隱層的神經元個數就是(1000*1000)/(10*10)=100*100個神經元了，假設步長是8，也就是卷積核會重疊兩個畫素，那麼我就不算了，思想懂了就好了。注意了，這只是一種濾波器，也就是一個Feature Map的神經元個數哦，如果100個Feature Map就是100倍了。由此可見，影像越大，神經元個數和需要訓練的權值引數個數的貧富差距就越大。

需要注意的一點是，上面的討論都沒有考慮每個神經元的偏置部分。所以權值個數需要加1。這個也是同一種濾波器共享的。

總之，卷積網路的核心思想是將：區域性感受野、權值共享（或者權值賦值）以及時間或空間亞取樣這三種結構思想結合起來獲得了某種程度的位移、尺度、形變不變性。

2.3The Full Model

卷積神經網路是一個多層的神經網路，每層由多個二維平面組成，而每個平面由多個獨立神經元組成。網路中包含一些簡單元和複雜元，分別記為S-元和C-元。S-元聚合在一起組成S-面，S-面聚合在一起組成S-層，用Us表示。C-元、C-面和C-層(Uc)之間存在類似的關係。網路中任意中間級由S-層與C-層串接而成，而輸入級只含一層，它直接接受二維視覺模式，樣本特徵提取步驟已嵌入到卷積神經網路模型的互聯結構中。

一般地，Us為特徵提取層（子取樣層）每個神經元的輸入與前一層的區域性感受野相連，並提取該區域性的特徵，一旦該區域性特徵被提取後，它與其他特徵之間的位置關係也隨之確定下來；Uc是特徵對映層（卷積層），網路的每個計算層由多個特徵對映組成，每個特徵對映為一個平面，平面上所有神經元的權值相等。特徵對映結構採用影響函式核小的sigmoid函式作為卷積函式的啟用函式，使得特徵對映具有位移不變性。此外，由於一個對映面上的神經元共享權值，因而減少了網路自由引數的個數，降低了網路引數選擇的複雜度。卷積神經網路中的每一個特徵提取層（S-層）都緊跟著一個用來求區域性平均與二次提取的計算層（C-層），這種特有的兩次特徵提取結構使網路在識別時對輸入樣本有較高的畸變容忍能力。

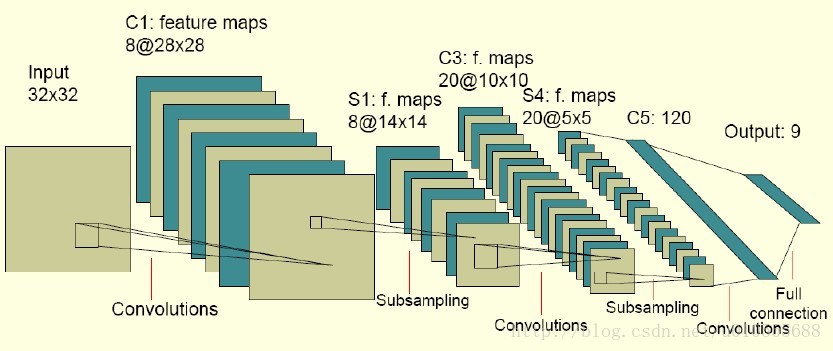
下面是一個卷積網路的例項：

圖中的卷積網路工作流程如下，輸入層由32×32個感知節點組成，接收原始影像。然後，計算流程在卷積和子抽樣之間交替進行，如下所述：

第一隱藏層進行卷積，它由8個特徵對映組成，每個特徵對映由28×28個神經元組成，每個神經元指定一個 5×5 的接受域，這28×28個神經元共享5×5個權值引數，即卷積核；

第二隱藏層實現子 抽樣和區域性平均，它同樣由 8 個特徵對映組成，但其每個特徵對映由14×14 個神經元組成。每個神經元具有一個 2×2 的接受域，一個可訓練係數，一個可訓練偏置和一個 sigmoid 啟用函式。可訓練係數和偏置控制神經元的操作點；

第三隱藏層進行第二次卷積，它由 20 個特徵對映組成，每個特徵對映由 10×10 個神經元組成。該隱藏層中的每個神經元可能具有和下一個隱藏層幾個特徵對映相連的突觸連線，它以與第一個卷積 層相似的方式操作。

第四個隱藏層進行第二次子抽樣和區域性平均汁算。它由 20 個特徵對映組成，但每個特徵對映由 5×5 個神經元組成，它以 與第一次抽樣相似的方式操作。

第五個隱藏層實現卷積的最後階段，它由 120 個神經元組成，每個神經元指定一個 5×5 的接受域。

最後是個全連線層，得到輸出向量。

相繼的計算層在卷積和抽樣之間的連續交替，我們得到一個“雙尖塔”的效果，也就是在每個卷積或抽樣層，隨著空 間解析度下降，與相應的前一層相位元徵對映的數量增加。卷積之後進行子抽樣的思想是受到動物視覺系統中的“簡單的”細胞後面跟著“複雜的”細胞的想法的啟發而產生的。

圖中所示的多層感知器包含近似 100000 個突觸連線，但只有大約2600 個自由引數(每個特徵對映為一個平面，平面上所有神經元的權值相等)。自由引數在數量上顯著地減少是通過權值共享獲得 的，學習機器的能力（以 VC 維的形式度量）因而下降，這又提高它的泛化能力。而且它對自由引數的調整通過反向傳播學習的隨機形式來實 現。另一個顯著的特點是使用權值共享使得以並行形式實現卷積網路變得可能。這是卷積網路對全連線的多層感知器而言的另一個優點。

3、CNN的訓練

神經網路用於模式識別的主流是有指導學習網路，無指導學習網路更多的是用於聚類分析。對於有指導的模式識別，由於任一樣本的類別是已知的，樣本在空間的分佈不再是依據其自然分佈傾向來劃分，而是要根據同類樣本在空間的分佈及不同類樣本之間的分離程度找一種適當的空間劃分方法，或者找到一個分類邊界，使得不同類樣本分別位於不同的區域內。這就需要一個長時間且複雜的學習過程，不斷地呼叫以劃分樣本空間的分類邊界的位置，使盡可能少的樣本被劃分到非同類區域中。

卷積網路在本質上是一種輸入到輸出的對映，它能夠學習大量的輸入與輸出之間的對映關係，而不需要任何輸入和輸出之間的精確的數學表示式，只要用已知的模式對卷積網路加以訓練，網路就具有輸入輸出對之間的對映能力。卷積網路執行的是有導師訓練，所以其樣本集是由形如：(輸入向量，理想輸出向量)的向量對構成的。所有這些向量對，都應該是來源於網路即將模擬的系統的實際“執行”結果。它們可以是從實際執行系統中採集來的。在開始訓練前，所有的權都應該使用一些不同的小隨機數進行初始化。“小隨機數”用來保證網路不會因為權值過大而進入飽和狀態，從而導致訓練失敗；“不同”用來保證網路可以正常地學習。實際上，如果用相同的數去初始化權矩陣，則網路無能力學習。

訓練演算法與傳統的BP演算法差不多。主要包括4步，這4步被分為兩個階段：

第一階段，向前傳播階段：

a）從樣本集中取一個樣本(X,Yp)，將X輸入網路；

b）計算相應的實際輸出Op。

在此階段，資訊從輸入層經過逐級的變換，傳送到輸出層。這個過程也是網路在完成訓練後正常執行時執行的過程。在此過程中，網路執行的是計算（實際上就是輸入與每層的權值矩陣相點乘，得到最後的輸出結果）：

O_p=F_n（…（F₂（F₁（X_pW^（1））W^（2））…）W^（n））

第二階段，向後傳播階段：

a）計算實際輸出Op與相應的理想輸出Yp的差；

b）按極小化誤差的方法反向傳播調整權矩陣。

4、CNN的學習

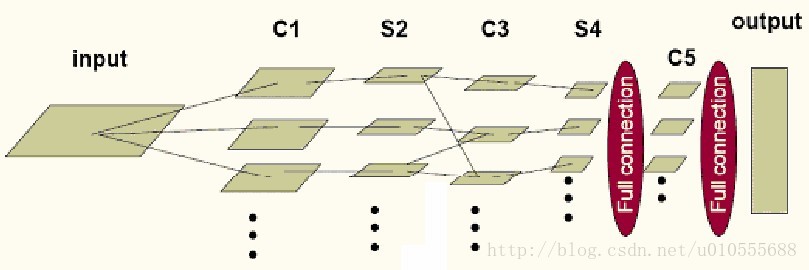
總體而言，卷積網路可以簡化為下圖所示模型：

其中，input到C1、S4到C5、C5到output是全連線，C1到S2、C3到S4是一一對應的連線，S2到C3為了消除網路對稱性，去掉了一部分連線，可以讓特徵對映更具多樣性。需要注意的是C5卷積核的尺寸要和S4的輸出相同，只有這樣才能保證輸出是一維向量。

4.1卷積層的學習

卷積層的典型結構如下圖所示：

卷積層的前饋運算是通過如下演算法實現的：

卷積層的輸出=sigmoid(sum(卷積)+偏移量)

其中卷積核和偏移量都是可訓練的。下面是其核心程式碼：

    ConvolutionLayer::fprop(input,output) {  
      //取得卷積核的個數  
      int n=kernel.GetDim(0);  
      for (int i=0;i<n;i++) {  
          //第i個卷積核對應輸入層第a個特徵對映，輸出層的第b個特徵對映  
          //這個卷積核可以形象的看作是從輸入層第a個特徵對映到輸出層的第b個特徵對映的一個連結  
          int a=table[i][0], b=table[i][1];  
          //用第i個卷積核和輸入層第a個特徵對映做卷積  
          convolution = Conv(input[a],kernel[i]);  
          //把卷積結果求和  
          sum[b] +=convolution;  
      }  
      for (i=0;i<(int)bias.size();i++) {  
          //加上偏移量  
          sum[i] += bias[i];  
      }  
      //呼叫Sigmoid函式  
      output = Sigmoid(sum);  
    }  

其中，input是n1*n2*n3的矩陣，n1是輸入層特徵對映的個數，n2是輸入層特徵對映的寬度，n3是輸入層特徵對映的高度。output、sum、convolution、bias是n1*(n2-kw+1)*(n3-kh+1)的矩陣，kw、kh是卷積核的寬度和高度（圖中是5*5）。kernel是卷積核矩陣。table是連線表。即如果第a輸入和第b輸出之間有連線，table裡就會有[a, b]這一項，而且每個連線都對應一個卷積核。

卷積層的反饋運算的核心程式碼如下：

    ConvolutionLayer::bprop(input,output,in_dx,out_dx) {  
      //梯度通過DSigmoid反傳  
      sum_dx = DSigmoid(out_dx);  
      //計算bias的梯度  
      for (i=0;i<bias.size();i++)  {  
          bias_dx[i] = sum_dx[i];  
      }  
      //取得卷積核的個數  
      int n=kernel.GetDim(0);  
      for (int i=0;i<n;i++)  
      {  
          int a=table[i][0],b=table[i][1];  
          //用第i個卷積核和第b個輸出層反向卷積（即輸出層的一點乘卷積模板返回給輸入層），並把結果累加到第a個輸入層  
          input_dx[a] += DConv(sum_dx[b],kernel[i]);  
          //用同樣的方法計算卷積模板的梯度  
          kernel_dx[i] += DConv(sum_dx[b],input[a]);  
      }  
    }  

其中in_dx、out_dx的結構和input、output相同，代表的是相應點的梯度。

4.2子取樣層的學習

子取樣層的典型結構如下圖所示：

類似的子取樣層的輸出的計算式為：

輸出=Sigmoid(取樣*權重+偏移量)

其核心程式碼如下：

    SubSamplingLayer::fprop(input,output) {  
      int n1= input.GetDim(0);  
      int n2= input.GetDim(1);  
      int n3= input.GetDim(2);  
      for (int i=0;i<n1;i++) {  
          for (int j=0;j<n2;j++) {  
              for (int k=0;k<n3;k++) {  
                  //coeff 是可訓練的權重，sw 、sh 是取樣視窗的尺寸。  
                  sub[i][j/sw][k/sh] += input[i][j][k]*coeff[i];  
              }  
          }  
      }  
      for (i=0;i<n1;i++) {  
          //加上偏移量  
          sum[i] = sub[i] + bias[i];  
      }  
      output = Sigmoid(sum);  
    }  

子取樣層的反饋運算的核心程式碼如下：

    SubSamplingLayer::bprop(input,output,in_dx,out_dx) {  
      //梯度通過DSigmoid反傳  
      sum_dx = DSigmoid(out_dx);  
      //計算bias和coeff的梯度  
      for (i=0;i<n1;i++) {  
          coeff_dx[i] = 0;  
          bias_dx[i] = 0;  
          for (j=0;j<n2/sw;j++)  
              for (k=0;k<n3/sh;k++) {  
                  coeff_dx[i] += sub[j][k]*sum_dx[i][j][k];  
                  bias_dx[i] += sum_dx[i][j][k]);  
              }  
      }  
      for (i=0;i<n1;i++) {  
          for (j=0;j<n2;j++)  
              for (k=0;k<n3;k++) {  
                  in_dx[i][j][k] = coeff[i]*sum_dx[i][j/sw][k/sh];  
              }  
      }  
    }  

5、CNN的優點

卷積神經網路CNN主要用來識別位移、縮放及其他形式扭曲不變性的二維圖形。由於CNN的特徵檢測層通過訓練資料進行學習，所以在使用CNN時，避免了顯式的特徵抽取，而隱式地從訓練資料中進行學習；再者由於同一特徵對映面上的神經元權值相同，所以網路可以並行學習，這也是卷積網路相對於神經元彼此相連網路的一大優勢。卷積神經網路以其區域性權值共享的特殊結構在語音識別和影像處理方面有著獨特的優越性，其佈局更接近於實際的生物神經網路，權值共享降低了網路的複雜性，特別是多維輸入向量的影像可以直接輸入網路這一特點避免了特徵提取和分類過程中資料重建的複雜度。

流的分類方式幾乎都是基於統計特徵的，這就意味著在進行分辨前必須提取某些特徵。然而，顯式的特徵提取並不容易，在一些應用問題中也並非總是可靠的。卷積神經網路，它避免了顯式的特徵取樣，隱式地從訓練資料中進行學習。這使得卷積神經網路明顯有別於其他基於神經網路的分類器，通過結構重組和減少權值將特徵提取功能融合進多層感知器。它可以直接處理灰度圖片，能夠直接用於處理基於影像的分類。

卷積網路較一般神經網路在影像處理方面有如下優點： a）輸入影像和網路的拓撲結構能很好的吻合；b）特徵提取和模式分類同時進行，並同時在訓練中產生；c）權重共享可以減少網路的訓練引數，使神經網路結構變得更簡單，適應性更強。

6、CNN的實現問題

CNNs中這種層間聯絡和空域資訊的緊密關係，使其適於影像處理和理解。而且，其在自動提取影像的顯著特徵方面還表現出了比較優的效能。在一些例子當中，Gabor濾波器已經被使用在一個初始化預處理的步驟中，以達到模擬人類視覺系統對視覺刺激的響應。在目前大部分的工作中，研究者將CNNs應用到了多種機器學習問題中，包括人臉識別，文件分析和語言檢測等。為了達到尋找視訊中幀與幀之間的相干性的目的，目前CNNs通過一個時間相干性去訓練，但這個不是CNNs特有的。 

由於卷積神經網路採用BP網路相同的演算法。所以，採用現有BP網路就可以實現。開源的神經網路程式碼FAAN可以利用。這個開源的實現採用了一些程式碼優化技術，有雙精度，單精度，定點運算三個不同的版本。

由於經典的BP網路是一個一維節點分佈排列，而卷積神經網路是二維網路結構。所以，要把卷積神經網路的每一層，按照一定的順序和規則對映為一維節點分佈，然後，按照這個分佈建立一個多層反向傳播演算法的網路結構，就可以按照一般的BP訓練演算法去學習網路引數。對於實際環境中新樣本的預測，也採用BP演算法中相同訊號前向傳遞演算法進行。具體細節也可以參考網上的一個開原始碼，連結如下：

http://www.codeproject.com/Articles/16650/Neural-Network-for-Recognition-of-Handwritten-Digi

注：這個程式碼在建立CNN的時候有個明顯的BUG，如果你看明白了我上面對簡化的LeNet-5的結構描述，一眼就會找出問題所在。