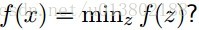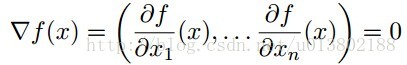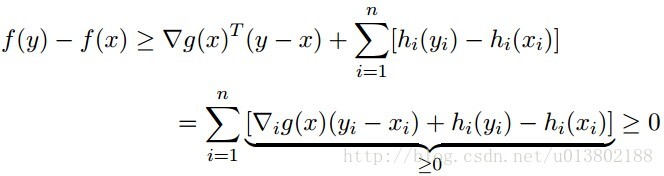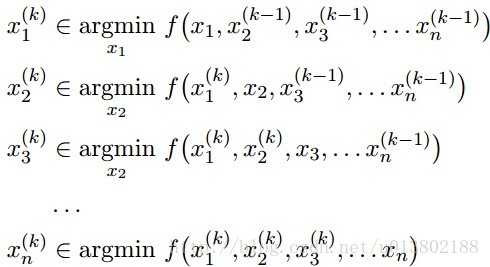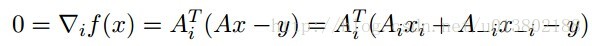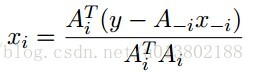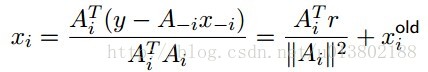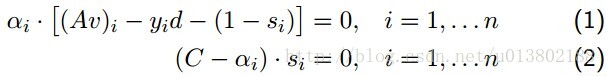(轉載)機器學習知識點(十二)座標下降法(Coordinate descent)

首先介紹一個演算法：coordinate-wise minimization

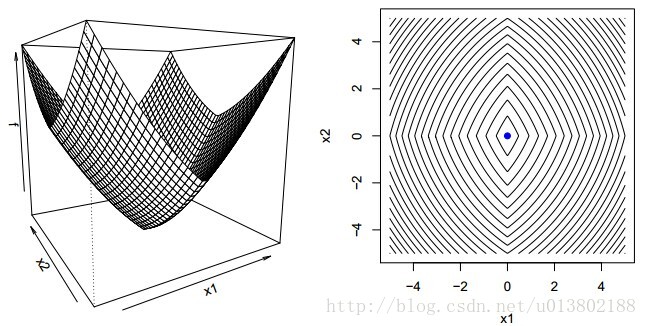
問題的描述：給定一個可微的凸函式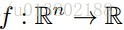，如果在某一點x，使得f(x)在每一個座標軸上都是最小值，那麼f(x)是不是一個全域性的最小值。

形式化的描述為：是不是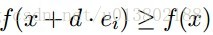對於所有的d，i都有

這裡的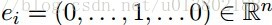代表第i個標準基向量。

答案為成立。

這是因為：

但是問題來了，如果對於凸函式f，若不可微該會怎樣呢？

答案為不成立，上面的圖片就給出了一個反例。

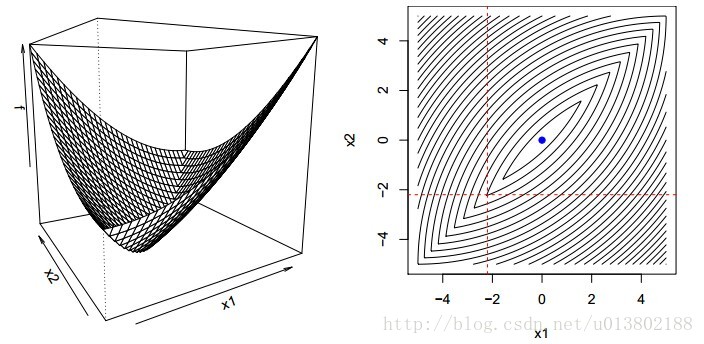
那麼同樣的問題，現在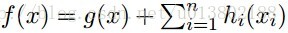，其中g是可微的凸函式，每一個hi都是凸的？

答案為成立。

證明如下，對每一個y

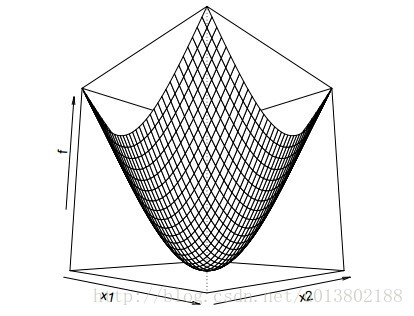
座標下降(Coordinate descent)：

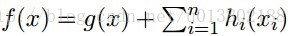
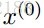
這就意味著，對所有的，其中g是可微的凸函式，每一個hi都是凸的，我們可以使用座標下降尋求一個最小值，我們從一個最初的猜想開始，對k進行迴圈：

每一次我們解決了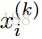，我們都會使用新的值。

Tseng (2001)的開創性工作證明：對這種f（f在緊集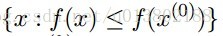上連續，且f到達了其最小值），的極限值，k=1,2,3….是f的一個最小元(minimizer)。

在實分析領域：

隨後收斂與x*( Bolzano-Weierstrass)

收斂於f*( monotoneconvergence)

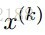
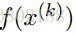
其中：

座標下降的順序是任意的，可以是從1到n的任意排列。

可以在任何地方將單個的座標替代成座標塊

關鍵在於一次一個地更新，所有的一起更新有可能會導致不收斂

我們現在討論一下座標下降的應用：

線性迴歸：

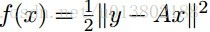
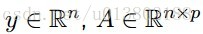
令，其中，A有p列：

最小化xi，對所有的xj，j不等於i：

解得：

座標下降重複這個更新對所有的

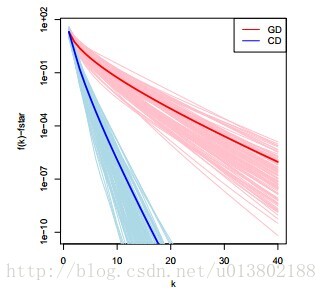
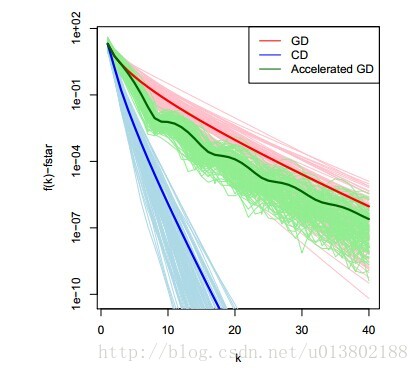
對比座標下降與梯度下降線上性迴歸中的表現（100個例項，n=100，p=20）

將座標下降的一圈與梯度下降的一次迭代對比是不是公平呢？是的。

其中r=y-Ax。每一次的座標更新需要O(n)個操作，其中O(n)去更新r，O(n)去計算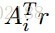，所以一圈就需要O(np)，跟梯度下降是一樣的。

我們用相同的例子，用梯度下降進行比較，似乎是與計算梯度下降的最優性相違背。

那麼座標下降是一個一階的方法嗎？事實上不是，它使用了比一階更多的資訊。

現在我們再關注一下支援向量機：

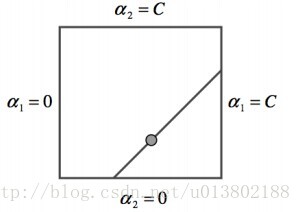
SVM對偶中的座標下降策略：

SMO(Sequentialminimal optimization)演算法是兩塊的座標下降，使用貪心法選擇下一塊，而不是用迴圈。

回撥互補鬆弛條件(complementaryslackness conditions)：

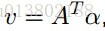
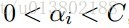
v，d，s是原始的係數，截距和鬆弛，其中，使用任何的（1）中i使得來計算d，利用（1）（2）來計算2.

SMO重複下面兩步：

選出不滿足互補鬆弛的αi，αj

最小化αi，αj使所有的變數滿足條件

第一步使用啟發式的方法貪心得尋找αi，αj，第二步使用等式約束。

——————維基百科的解釋——————

座標下降優化方法是一種非梯度優化演算法。為了找到一個函式的區域性極小值，在每次迭代中可以在當前點處沿一個座標方向進行一維搜尋。在整個過程中迴圈使用不同的座標方向。一個週期的一維搜尋迭代過程相當於一個梯度迭代。

座標下降法基於最小化多變數目標函式可以通過每次沿一個方向最小化目標函式來求解。與梯度方法的變化的梯度方向不同，座標下降方法固定其他的梯度方向。例如，座標方向為e₁,e₂,…,e_n。每次沿一個座標方向最小化目標函式，迴圈地沿每個座標方向進行計算。如果給定X^k，X^k+1的第i個座標由如下給定：

從初始值X₀求取F的區域性值，然後迭代的求取一個序列X₀，X₁，X₂，…

通過在每次迭代中進行一維搜尋，可以有如下結論：

It can be shown that this sequence has similar convergence properties as steepest descent. No improvement after one cycle of line search along coordinate directions implies a stationary point is reached.

This process is illustrated below.

    其實，gradient descent 方法是利用目標函式的導數（梯度）來確定搜尋方向的，而該梯度方向可能不與任何座標軸平行。而coordinate descent方法是利用當前座標系統進行搜尋，不需要求目標函式的導數，只按照某一座標方向進行搜尋最小值。