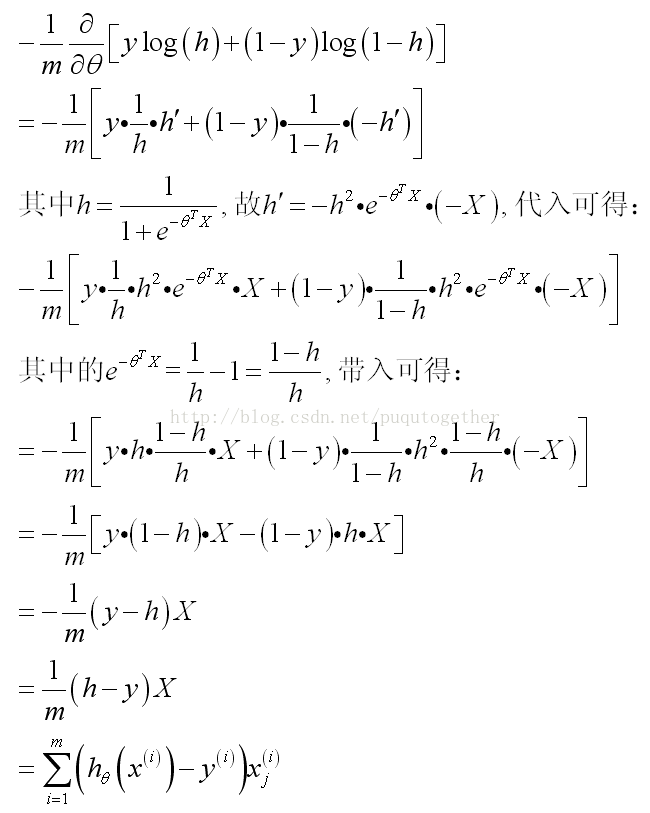Stanford機器學習課程筆記——LR的公式推導和過擬合問題解決方案

    

1. Logistic Regression

    前面說的單變數線性迴歸模型和多變數線性迴歸模型，它們都是線性的迴歸模型。實際上，很多應用情況下，資料的模型不是一個簡單的線性表示就可以搞定的（後面的稀疏表示和字典學習又再次回到的線性表示，當然這個是後話）。更多的時候，我們需要建立一個非線性的模型。此時，Logistic Regression就誕生了。

    LR的假設模型：

    前面的線性模型都是線性方程作為假設模型，這裡的LR使用的邏輯函式，又稱為S型函式。

為什麼使用這個邏輯函式呢？其實後面有著既內涵有巧妙地原因：

• 這個函式對於給定的輸入變數，會根據選擇的引數計算輸出變數=1的可能性，，也就是說它的輸出表示概率，都是0到1之間；
• 該S型假設模型函式融入到後面的代價函式中之後，在梯度下降法中求導之後的模型，巧妙地和前面線性模型的求導形式一致。

    LR的代價函式：

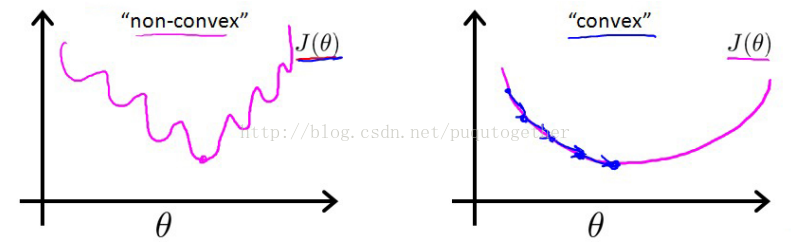
    有了前面的假設，我們當然可以使用之前熟悉的誤差平方和來作為代價函式。但是，我們會發現這時候的代價函式是非凸的，也就是函式影像中會出現許多的區域性最小值，導致梯度下降法極其容易得到區域性最小值。如下：

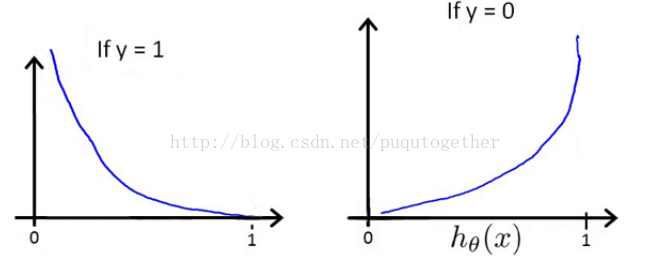
所以，我們需要重新設定代價函式形式。LR中的代價函式如下：

選擇這樣子的代價函式的原因如下：

• 當實際的y=1和預測的h_theta也為1的時候，誤差=0，誤差會隨著h_theta的變小而增大；當y=0和h_theta=0的時候，誤差=0,誤差會隨著h_theta的增大而增大；
• 代價函式的求導形式和線性模型的求導形式巧妙的相似。（這部分有兩個原因，前面已經提到一個了）

2. LR的梯度下降法公式推導

    給定上面定義的假設和代價函式，而且此時的代價函式也是非凸的，我們便可以使用梯度下降法求出令代價函式最小時的theta向量。梯度下降法的基本演算法如下：

此時關鍵的時候要把J_theta對theta的導數求出來。具體的公式推導比較複雜，如下：

（其中的假設我直接用h簡單表示）

然後，LR的梯度下降演算法就成為了：

發現這個形式和前面線性迴歸模型的梯度下降法巧妙的一致了。

當然，後面我們就可以使用這個演算法來求解LR模型了。

3. 解決過擬合問題

    什麼是過擬合問題？就是我們訓練出來的模型可以很好的適應所有的訓練樣本，但是不能對測試樣本很好地預測，這就是過擬合問題。如下圖所示：

解決過擬合的方法有兩個：

（1） 降維，可以使用PCA演算法把樣本的維數降低，使得模型的theta的個數減少，次數也會降低，避免了過擬合；

（2） 正則化，設計正則項regularization term, 也可以避免過擬合。這種方法下面詳細說一下。

正則化的方式有幾種：

1. 可以給一些引數項加懲罰；

     比如下面的模型：

由於高次項的theta_3和theta_4比較大，所以我們需要對這兩項乘以懲罰，也就是在代價函式的後面對這兩個theta_3和theta_4加一個很大的權重。

    那麼當我們不知道哪幾項需要懲罰的時候，我們就會在代價函式中給每一項的theta都加一個懲罰，稱為給代價函式加一個正則項。如下：

同樣地，對於LR迴歸，我們也可以在它的代價函式後面新增一個正則項，這樣子我們也可以避免過擬合。

    其實，每次更新theta的時候，都會額外減去一個(lambda/m)*theta_j。這樣會使得求解出來的theta普遍小一下。但是，我們要注意正則項前面的因子lambda的設定，如果lambda設定過大，會導致求解出來的所有theta都很小，甚至等於0 。