轉載請註明出處:http://www.cnblogs.com/Joanna-Yan/p/5094764.html
總結下常用的排序演算法,方便以後查閱。
常見排序演算法:氣泡排序、選擇排序、插入排序、殼(shell)排序、合併排序、快速排序、堆排序。
要選擇合適的演算法,需考慮的因素:執行時間、儲存空間和程式設計工作。
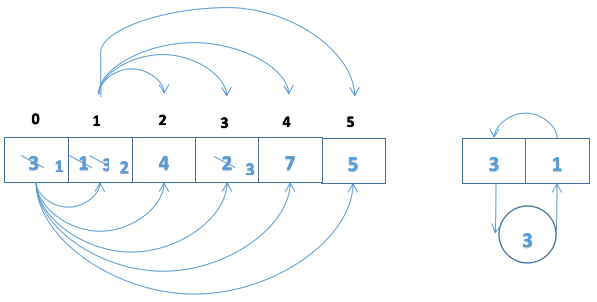
1、選擇排序
具有二次方程增長階,近適用於小列表排序。
通過列表反覆掃描,每次掃描選擇一項,然後將這一項移動到列表中正確的位置。
選擇排序總比較次數=(n-1)+(n-2)+(n-3)+...+3+2+1
=n(n-1)/2
n(n-1)/2是O(n^2)階的級,所以選擇排序是階O(n^2)的演算法。
//外迴圈控制行(迴圈比較次數) for (int i = 0; i < arr.length-1; i++) { //內迴圈控制列,前後兩個比較 for (int j = i+1; j < arr.length; j++) { if(arr[i]>arr[j]){ int temp=arr[i]; arr[i]=arr[j]; arr[j]=temp; } } }
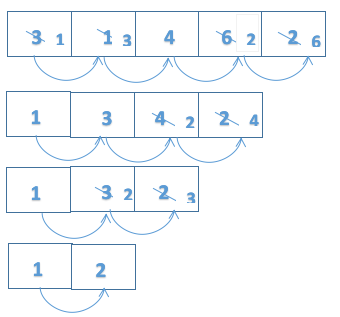
2、冒泡演算法
相鄰兩個元素進行比較,如果符合條件就換位。
氣泡排序總比較次數=(n-1)+(n-2)+(n-3)+...+3+2+1
=n(n-1)/2
n(n-1)/2是O(n^2)階的級,所以氣泡排序是階O(n^2)的演算法。
//最後一個元素不需要比較 for (int i = 0; i < arr.length-1; i++) { //-i:讓每次比較的元素減少;-1避免下標越界,即當j=4時,j+1就越界了 for (int j = 0; j < arr.length-i-1; j++) { if(arr[j]>arr[j+1]){ int temp=arr[j]; arr[j]=arr[j+1]; arr[j+1]=temp; } }
}
3、快速排序
基本思想:
(1)先從數列中取出一個數作為基準數(一般取區間第一個數)
(2)區分過程,將比這個數大的數全放在它的右邊,小於或等於它的數放到它的左邊。
(3)再對各區間重複第二步,直到各區間只有一個數。
這裡的例子我們用挖坑填數發來說明:
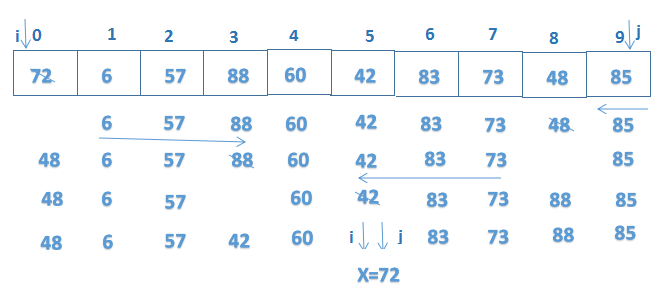
再對a[0-4]和a[6-9]這兩個子區間重複上述步驟就可以了,先從後向前找,再從前向後找。
對挖坑填數進行總結:
1. i=l,j=r,將基準數挖出形成第一個坑a[i];
2. j--由後向前找比它小的數,找到後挖出此數,填前一個坑a[i]中;
3. i++由前向後找比它大的數,找到後也挖出次數填到前一個坑a[j]中。
4. 在重複執行2,3兩步,直到i==j,將基準數填入a[i]中。
void quick_sort(int s[],int l,int r){ if(l<r){ int i=l,j=r,x=s[l]; while(i<j){ while(i<j&&s[j]>=x){j--;}//從右向左找第一個小於x的數 if(i<j){s[i++]=s[j];} while(i<j&&s[i]<x){i++;}//從左到右找第一個大於等於x的數 if(i<j){s[j--]=s[j];} } s[i]=x; quick_sort(s,l,i-1);//遞迴 quick_sort(s,i-1,r); } }
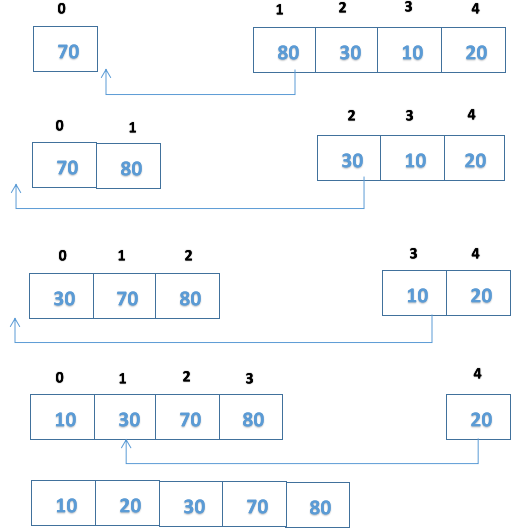
4、插入排序
具有二次方程增長階,僅用於小列表排序。
如果需要排序的列表幾乎已經排序,則插入排序比氣泡排序和選擇排序更有效率。
插入排序執行不同次數的比較,這取決於最初的元素分階,當元素已經處於排序階,則插入排序需要進行極少比較。

需將列表分為兩個子列表,即排序和未排序。
排序列表 未排序列表
for (int i = 0; i < arr.length; i++) {//假設第一個元素放到了正確的位置上,這樣僅需遍歷1~n-1 int j=i; int target=arr[i]; while(j>0&&target<arr[j-1]){ arr[j]=arr[j-1]; j--; } arr[j]=target; }
最佳用例效率:O(n),當列表已經被排序時,產生最佳用例。
最差用例效率:O(n^2),當列表反向順序排列時,產生最差用例。
5.殼(Shell)排序
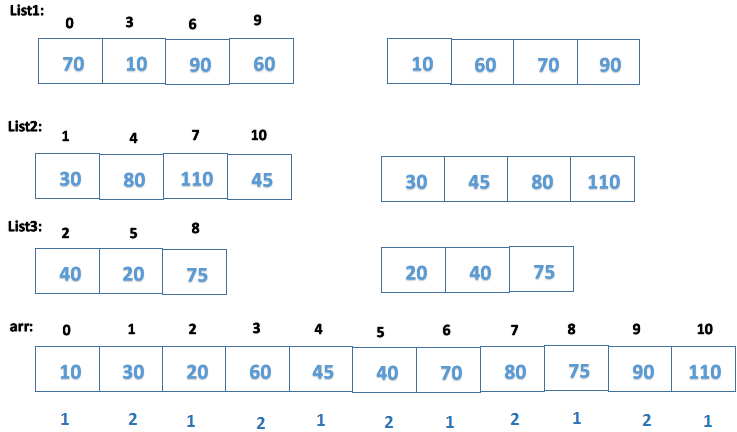
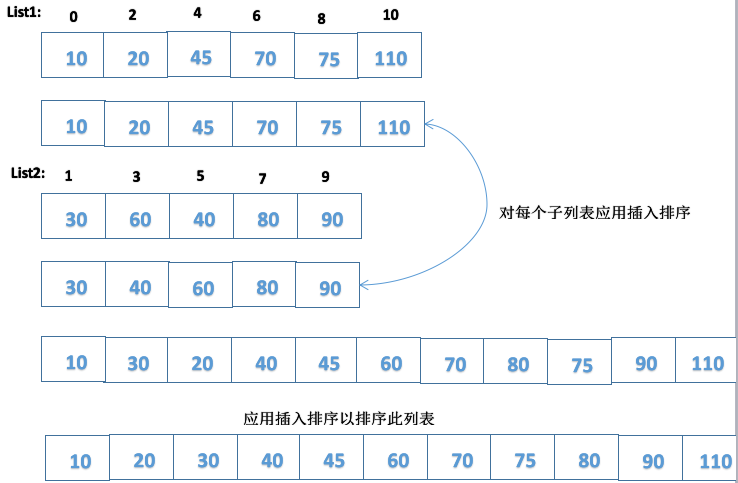
通過若干位置的距離形成多個子列表分隔元素並進行比較來改進插入排序演算法。對每個子列表應用插入排序時元素朝著其正確的位置移動,減少了比較次數。

-------選擇分隔組中元素的距離以形成多個子列表。(這裡為3)
-------對每個子列表應用插入排序使元素朝著其正確的位置移動。
6.堆排序
堆排序與快速排序、歸併排序一樣都是時間複雜度為O(nlogn)的幾種常見排序。
若將堆視為一個完全二叉樹,則堆的含義為:完全二叉樹中有非葉結點(ri)均不大於(後不小於)其左孩子的值(r(2)i),右孩子的值(r(2i+1))。
堆定義是:n個關鍵字序列k1,k2,k3,...kn稱為堆,當且僅當該序列滿足如下性質:
(1)ki<=k(2i)且ki<=k(2i+1)或
(2)ki>=k(2i)且ki>=k(2i+1) (1<=i<=[n/2])
即孩子結點>=雙親結點 或 孩子結點<=雙親結點
eg:{6,8,7,9,01,3,2,4,5}說明採用堆排序方法進行排序的過程。

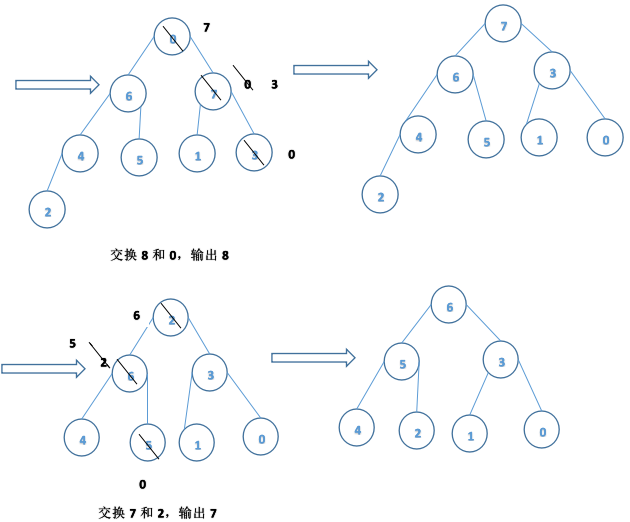
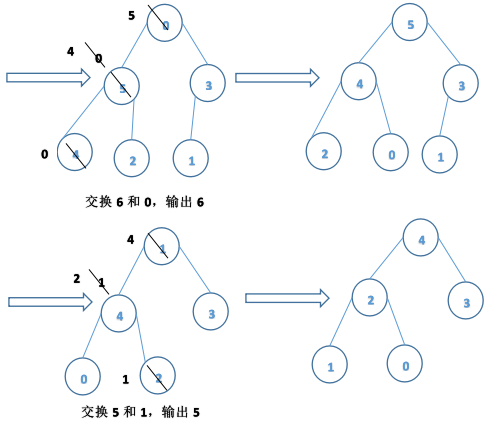

輸出:9,8,7,6,5,4,3,2,1,0
7.歸併排序
多次將若干個已經排序好的有序表合併成一個有序表。直接將兩個表合併的歸併成為二路歸併。
eg:{18,2,20,34,12,32,6,16}說明歸併排序方法進行排序的過程。
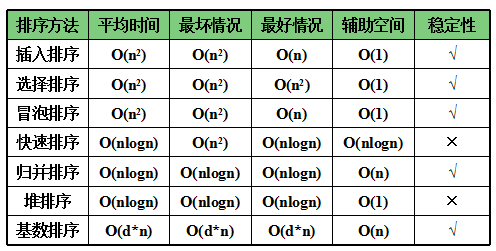
時間特性說明:
時間複雜度O(nlogn):快速、堆、歸併排序。快速最快,在n較大時,歸併較堆更快。
時間複雜度為O(n^2):插入、冒泡、選擇排序。插入最常用,尤其基本有序時,選擇記錄移動次數最少。
當待排序記錄有序時:插入和冒泡可達到O(n),快速蛻化到O(n^2).
選擇、堆、歸併排序的時間特性不隨關鍵字分佈而改變。
如果此文對您有幫助,微信打賞我一下吧~
