使用鄰接矩陣的時間複雜度為O(n^2),用優先佇列的複雜度為O((m+n)logn)近似為O(mlogn)

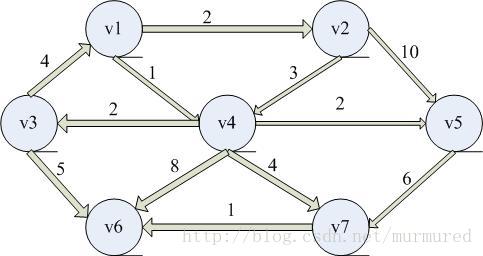
(一)  過程

每次選擇一個未訪問過的到已經訪問過（標記為Known）的所有點的集合的最短邊，並用這個點進行更新，過程如下：

Dv為最短路，而Pv為前面的頂點。

1.     初始

2.     在v1被標記為已知後的表

3.     下一步選取v4並且標記為known，頂點v3,v5,v6,v7是鄰接的頂點，而他們實際上都需要調整。如表所示:

4.     接下來選取v2,v4是鄰接點，但已經是known的，不需要調整，v5是鄰接的點但不做調整，因為經過v2的值為2+10=12而長為3的路徑已經是已知的。

5.     接下來選取v5，值為3，v7 3+6>5不需調整，然後選取v3，對v6的距離下調到3+5=8

6.     再選下一個頂點是v7，v6變為5+1=6

7.     最後選取v6

(二)  侷限性

Dijkstra沒辦法解決負邊權的最短路徑，如圖

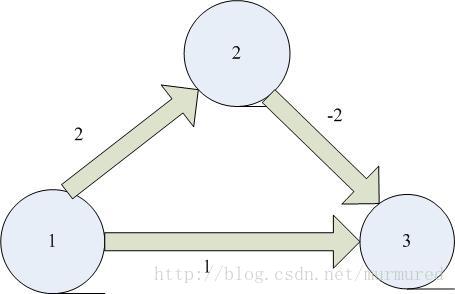
執行完該演算法後，從頂點1到頂點3的最短路徑為1,3，其長度為1，而實際上最短路徑為1,2,3，其長度為0.（因為過程中先選擇v3，v3被標記為已知，今後不再更新）

(三) 演算法實現。

1．普通的鄰接表 以（HDU 1874 暢通工程續 SPFA || dijkstra）為例

用vis作為上面標記的known，dis記錄最短距離（記得初始化為一個很大的數）。

void dijkstra(int s)
{
	memset(vis,0,sizeof(vis));       
	int cur=s;                   
	dis[cur]=0;
	vis[cur]=1;
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)                     
			if(!vis[j] && dis[cur] + map[cur][j] < dis[j])   //未被標記且比已知的短，可更新
				dis[j]=dis[cur] + map[cur][j] ;

		int mini=INF;
		for(int j=0;j<n;j++)                  
			if(!vis[j] && dis[j] < mini)    //選擇下一次到已知頂點最短的點。
				mini=dis[cur=j];
		vis[cur]=true;
	}	
}

要過載個比較函式.

struct point
{
	int val,id;
	point(int id,int val):id(id),val(val){}
	bool operator <(const point &x)const{
		return val>x.val;
	}
};
void dijkstra(int s)
{
	memset(vis,0,sizeof(vis));
	for(int i=0;i<n;i++)
		dis[i]=INF;	

	priority_queue<point> q;
	q.push(point(s,0));
	dis[s]=0;
	while(!q.empty())
	{
		int cur=q.top().id;
		q.pop();
		if(vis[cur]) continue;
		vis[cur]=true;
		for(int i=head[cur];i!=-1;i=e[i].next)
		{
			int id=e[i].to;
			if(!vis[id] && dis[cur]+e[i].val < dis[id])
			{
				dis[id]=dis[cur]+e[i].val;
				q.push(point(id,dis[id]));
			}
		}		
	}
}

void SPFA(int s)  
{  
    for(int i=0;i<n;i++)  
        dis[i]=INF;  
  
    bool vis[MAXN]={0};  
      
    vis[s]=true;  
    dis[s]=0;  
      
    queue<int> q;  
    q.push(s);  
    while(!q.empty())  
    {  
        int cur=q.front();  
        q.pop();  
        vis[cur]=false;  
        for(int i=0;i<n;i++)  
        {  
            if(dis[cur] + map[cur][i] < dis[i])  
            {  
                dis[i]=dis[cur] + map[cur][i];  
                if(!vis[i])  
                {  
                    q.push(i);  
                    vis[i]=true;  
                }  
            }             
        }  
    }  
}  

void spfa(int s)
{
	memset(vis,0,sizeof(vis));
	for(int i=0;i<n;i++)
		dis[i]=INF;	

	queue<int> q;
	q.push(s);
	vis[s]=true;
	dis[s]=0;
	while(!q.empty())
	{
		int cur=q.front();
		q.pop();
		vis[cur]=false;
		for(int i=head[cur];i!=-1;i=e[i].next)
		{
			int id=e[i].to;
			if(dis[id] > dis[cur]+e[i].val)
			{
				dis[id] = dis[cur] + e[i].val;
				if(!vis[id])
				{
					vis[id]=true;
					q.push(id);
				}
			}
		}
	}
}

bool spfa()  
{  
    for(int i=0;i<=n;i++)  
        dis[i]=INF;  
  
    bool vis[MAXN]={0};  
    int cnt[MAXN]={0};  
    queue<int> q;  
    dis[0]=0;  
    vis[0]=true;  
    cnt[0]=1;  
    q.push(0);  
  
    while(!q.empty())  
    {  
        int cur=q.front();  
        q.pop();  
        vis[cur]=false;  
  
        for(int i=head[cur];i!=-1;i=e[i].next)  
        {  
            int id=e[i].to;  
            if(dis[cur] + e[i].val > dis[id])  
            {  
                dis[id]=dis[cur]+e[i].val;  
                if(!vis[id])  
                {  
                    cnt[id]++;  
                    if(cnt[cur] > n)  
                        return false;  
                    vis[id]=true;  
                    q.push(id);  
                }  
            }  
        }  
    }  
    return true;  
} 

（三）：優化

void floyd()
{
    for(int k=0;k<n;k++)
		for(int i=0;i<n;i++)
			for(int j=0;j<n;j++)
				dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}