[Offer收割]程式設計練習賽1 hihocoder 1268 九宮 (DFS)

_TCgogogo_發表於2016-03-07
程式設計
時間限制:10000ms
單點時限:1000ms
記憶體限制:256MB

描述

小Hi最近在教鄰居家的小朋友小學奧數，而最近正好講述到了三階幻方這個部分，三階幻方指的是將1~9不重複的填入一個3*3的矩陣當中，使得每一行、每一列和每一條對角線的和都是相同的。

三階幻方又被稱作九宮格，在小學奧數裡有一句非常有名的口訣：“二四為肩，六八為足，左三右七，戴九履一，五居其中”，通過這樣的一句口訣就能夠非常完美的構造出一個九宮格來。

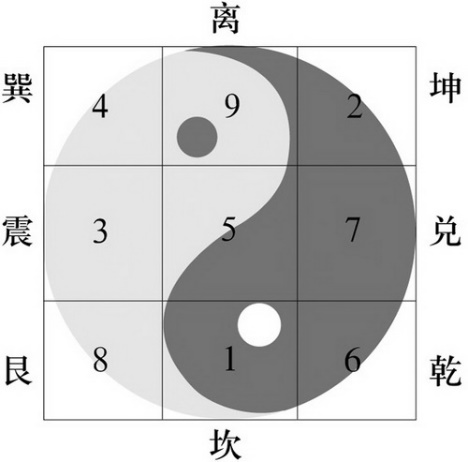
有意思的是，所有的三階幻方，都可以通過這樣一個九宮格進行若干映象和旋轉操作之後得到。現在小Hi準備將一個三階幻方（不一定是上圖中的那個）中的一些陣列抹掉，交給鄰居家的小朋友來進行還原，並且希望她能夠判斷出究竟是不是隻有一組解。

而你呢，也被小Hi交付了同樣的任務，但是不同的是，你需要寫一個程式~

輸入

輸入僅包含單組測試資料。

每組測試資料為一個3*3的矩陣，其中為0的部分表示被小Hi抹去的部分。

對於100%的資料，滿足給出的矩陣至少能還原出一組可行的三階幻方。

輸出

如果僅能還原出一組可行的三階幻方，則將其輸出，否則輸出“Too Many”（不包含引號）。

樣例輸入 
0 7 2
0 5 0
0 3 0
樣例輸出 
6 7 2
1 5 9
8 3 4

題目連結：http://hihocoder.com/problemset/problem/1268


題目分析：裸DFS

#include <cstdio>
#include <cstring>
int x[5][5], ans[5][5];
bool has[10];
int cnt, tmp;
bool flag;

bool ok()
{
    int sum = x[1][1] + x[1][2] + x[1][3];
    if(x[2][1] + x[2][2] + x[2][3] != sum)
        return false;
    if(x[3][1] + x[3][2] + x[3][3] != sum)
        return false;
    if(x[1][1] + x[2][1] + x[3][1] != sum)
        return false;
    if(x[1][2] + x[2][2] + x[3][2] != sum)
        return false;
    if(x[1][3] + x[2][3] + x[3][3] != sum)
        return false;
    if(x[1][1] + x[2][2] + x[3][3] != sum)
        return false;
    if(x[1][3] + x[2][2] + x[3][1] != sum)
        return false;
    return true;
}

void DFS(int i, int j)
{
    if(i == 4 && ok())
    {
        cnt ++;
        if(cnt == 1)
            memcpy(ans, x, sizeof(x));
        return;
    }
    if(x[i][j])
    {
        if(j == 3)
            DFS(i + 1, 1);
        else
            DFS(i, j + 1);
    }
    else
    {
        for(int num = 1; num <= 9; num++)
        {
            if(!has[num])
            {
                has[num] = true;
                x[i][j] = num;
                if(j == 3)
                    DFS(i + 1, 1);
                else
                    DFS(i, j + 1);
                has[num] = false;
                x[i][j] = 0;
            }
        }
    }
}

int main()
{
    cnt = 0;
    flag = false;
    for(int i = 1; i <= 3; i++)
    {
        for(int j = 1; j <= 3; j++)
        {
            scanf("%d", &x[i][j]);
            has[x[i][j]] = true;
        }
    }
    DFS(1, 1);
    if(cnt == 1)
        for(int i = 1; i <= 3; i++)
            for(int j = 1; j <= 3; j++)
                printf("%d%c", ans[i][j], j == 3 ? '\n' : ' ');
    else
        printf("Too Many\n");
}


相關文章