POJ 2528 Mayor's posters (線段樹區間更新 + 離散化)
Mayor's posters
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 52874 | Accepted: 15402 |
Description
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters
and introduce the following rules:
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.
- Every candidate can place exactly one poster on the wall.
- All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
- The wall is divided into segments and the width of each segment is one byte.
- Each poster must completely cover a contiguous number of wall segments.
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.
Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among
the n lines contains two integer numbers li and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= li <= ri <= 10000000. After
the i-th poster is placed, it entirely covers all wall segments numbered li, li+1 ,... , ri.
Output
For each input data set print the number of visible posters after all the posters are placed.
The picture below illustrates the case of the sample input.
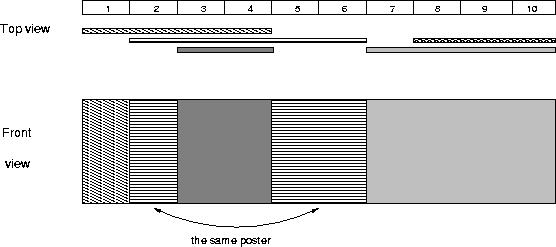
The picture below illustrates the case of the sample input.

Sample Input
1 5 1 4 2 6 8 10 3 4 7 10
Sample Output
4
Source
Alberta Collegiate Programming Contest 2003.10.18
題目大意:後貼的海報覆蓋先貼的,問最後區間能看到幾張海報(不一定要看到整張)
題目分析:開始剛好理解錯,當成後貼的放在先貼的下面了,wa成狗,不過不要緊,直接把for迴圈順序變一下就行了,由於區間範圍太大,直接建樹肯定gg,所以採用離散化,sort+unique不要太方便,這題資料很神奇,用map的時間是用陣列的10倍,用陣列的記憶體是用map的10倍,不過都可過~
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <map>
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
using namespace std;
int const MAX = 1e4 + 5;
int const MAXM = 1e7 + 5;
//map <int, int> chg;
int chg[MAXM];
int x[MAX * 2];
bool col[MAX << 2];
struct DATA
{
int l, r;
}d[MAX];
void PushUp(int rt)
{
col[rt] = (col[rt << 1] & col[rt << 1 | 1]);
}
void PushDown(int rt)
{
if(col[rt])
{
col[rt << 1] = col[rt];
col[rt << 1 | 1] = col[rt];
col[rt] = false;
}
}
bool Update(int L, int R, int l, int r, int rt)
{
if(L <= l && r <= R)
{
if(!col[rt])
{
col[rt] = true;
return true;
}
return false;
}
bool f = false;
PushDown(rt);
int mid = (l + r) >> 1;
if(L <= mid)
f |= Update(L, R, lson);
if(mid < R)
f |= Update(L, R, rson);
PushUp(rt);
return f;
}
int main()
{
int T;
scanf("%d", &T);
while(T --)
{
memset(col, false, sizeof(col));
int n, ans = 0, cnt = 0;
scanf("%d", &n);
for(int i = 0; i < n; i++)
{
scanf("%d %d", &d[i].l, &d[i].r);
x[cnt ++] = d[i].l;
x[cnt ++] = d[i].r;
}
sort(x, x + cnt);
cnt = unique(x, x + cnt) - x;
for(int i = 0; i < cnt; i++)
chg[x[i]] = i + 1;
for(int i = n - 1; i >= 0; i--)
if(Update(chg[d[i].l], chg[d[i].r], 1, cnt, 1))
ans ++;
printf("%d\n", ans);
}
}相關文章
- POJ 2528 Mayor's posters (線段樹 區間更新+離散化)
- POJ 2582 Mayor's posters 線段樹入門題+離散化
- POJ 3468 A Simple Problem with Integers (線段樹 區間更新)
- POJ 3468-A Simple Problem with Integers(區間更新線段樹)
- 【dp+離散化+線段樹優化】Paint優化AI
- POJ 3468 A Simple Problem with Integers(線段樹區間操作)
- hihocoder 1078 線段樹的區間修改 (線段樹 區間更新 模板)
- POJ 3468 A Simple Problem with Integers (線段樹 區間共加)
- POJ 3468 【區間修改+區間查詢 樹狀陣列 | 線段樹 | 分塊】陣列
- HDU 1698 Just a Hook (線段樹區間更新)Hook
- Codeforces 52C (線段樹區間更新)
- POJ 2777-Count Color(線段樹-區間染色查詢)
- 區間k小值(可持久化線段樹)持久化
- POJ 3264-Balanced Lineup詳解(線段樹區間求值)
- poj 3237 樹鏈剖分(區間更新,區間查詢)
- Codeforces 272C Dima and Staircase (線段樹區間更新 或 線性掃)AI
- 線段樹(3)——區間操作疊加
- hdu 2665 可持久化線段樹求區間第K大值(函式式線段樹||主席樹)持久化函式
- 芻議線段樹 2 (區間修改,區間查詢)
- 線段樹維護區間等差數列
- HDU 1754 I Hate It (線段樹 區間最值)
- Java 演算法-區間求和I(線段樹)Java演算法
- Leetcode 327. 區間和的個數 (字首和 + 離散化 + 樹狀陣列)LeetCode陣列
- POJ 1195-Mobile phones(二維樹狀陣列-區間更新區間查詢)陣列
- hdu4288 離線處理線段樹
- POJ 2991 Crane(線段樹+計算幾何)
- HDU 5862 Counting Intersections(樹狀陣列+掃描線+離散化)陣列
- hdu4325 樹狀陣列+離散化陣列
- 1082 線段樹練習 3 區間查詢與區間修改
- 離散化
- 可持久化線段樹持久化
- (poj3468)A Simple Problem with Integers(區間更新)
- POJ 2777 Count Color 線段樹入門題
- 區間演算法題用線段樹可以秒解?演算法
- POJ 2828 Buy Tickets 線段樹入門(建樹稍微有點抽象)抽象
- HDU1698 Just a Hook【線段樹基礎:區間修改+區間查詢】Hook
- POJ 1418 圓的基本操作以及 圓弧離散化
- 線段樹學習筆記(更新中)筆記