POJ 3565 Ants (最小權完美匹配 KM演算法)

_TCgogogo_發表於2015-10-08
演算法
Ants
Time Limit: 5000MS   Memory Limit: 65536K
Total Submissions: 5583   Accepted: 1730   Special Judge

Description

Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself.

Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies.

Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection.

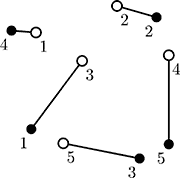
On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines.

Input

The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (−10 000 ≤ x, y ≤ 10 000) on a Cartesian plane. All ant colonies and apple trees occupy distinct points on a plane. No three points are on the same line.

Output

Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony.

Sample Input

5
-42 58
44 86
7 28
99 34
-13 -59
-47 -44
86 74
68 -75
-68 60
99 -60

Sample Output

4
2
1
5
3

Source

Northeastern Europe 2007

題目連結：http://poj.org/problem?id=3565

題目大意：n個白點和n個黑點，用n條不相交的線段把它們連線起來，求一個不相交的完美匹配的方案

題目分析：根據三角形兩邊之和大於第三邊可以證明最小權匹配是不相交的，然後就是模板了

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int const MAX = 105;
int const INF = 0x3fffffff;
double const EPS = 1e-6;
int n;
int visx[MAX], visy[MAX], lk[MAX], ans[MAX];
double lx[MAX], ly[MAX], w[MAX][MAX], slack[MAX];

struct POINT
{
    double x, y;
}p[MAX * 2];

double dis(POINT a, POINT b)
{
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
} 

int DFS(int x)
{
    visx[x] = 1;
    for(int y = 1; y <= n; y++)
    {
        if(visy[y])
            continue;
        double t = lx[x] + ly[y] - w[x][y];
        if(t < EPS)      
        {
            visy[y] = 1;
            if(lk[y] == -1 || DFS(lk[y]))
            {
                lk[y] = x;
                return 1;
            }
        }
        else if(slack[y] - t > EPS) 
            slack[y] = t;
    }
    return 0;
}

void KM()
{
    memset(lk, -1, sizeof(lk));
    memset(ly, 0, sizeof(ly));
    memset(lx, 0, sizeof(lx));
    for(int i = 1; i <= n; i++)          
        for(int j = 1; j <= n; j++)
            if(w[i][j] > lx[i])
                lx[i] = w[i][j];
    for(int x = 1; x <= n; x ++)
    {
        for(int i = 1; i <= n; i ++)
            slack[i] = INF;
        while(true)
        {
            memset(visx, 0, sizeof(visx));
            memset(visy, 0, sizeof(visy));
            if(DFS(x))    
                break;  
            double d = INF;
            for(int i = 1; i <= n; i++)
                if(!visy[i] && d > slack[i])
                    d = slack[i];
            for(int i = 1; i <= n; i++)
                if(visx[i])
                    lx[i] -= d;
            for(int i = 1; i <= n; i++) 
            {
                if(visy[i])
                    ly[i] += d;
                else
                    slack[i] -= d;
            }
        }
    }
}

int main ()
{
    while(scanf("%d", &n) != EOF)
    {
        memset(w, 0, sizeof(w));
        for(int i = 1; i <= 2 * n; i++)
            scanf("%lf %lf", &p[i].x, &p[i].y);
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                w[i][j] -= dis(p[i], p[j + n]);
        KM();
        for(int i = 1; i <= n; i++)
            ans[lk[i]] = i;
        for(int i = 1; i <= n; i++)
            printf("%d\n", ans[i]);
    }
}

相關文章