Codeforces Round #323 (Div. 2) (ABCD題解)

_TCgogogo_發表於2015-10-08

比賽連結：http://codeforces.com/contest/583


A. Asphalting Roads
time limit per test
1 second
memory limit per test
256 megabytes

City X consists of n vertical and n horizontal infinite roads, forming n × n intersections. Roads (both vertical and horizontal) are numbered from 1 to n, and the intersections are indicated by the numbers of the roads that form them.

Sand roads have long been recognized out of date, so the decision was made to asphalt them. To do this, a team of workers was hired and a schedule of work was made, according to which the intersections should be asphalted.

Road repairs are planned for n2 days. On the i-th day of the team arrives at the i-th intersection in the list and if none of the two roads that form the intersection were already asphalted they asphalt both roads. Otherwise, the team leaves the intersection, without doing anything with the roads.

According to the schedule of road works tell in which days at least one road will be asphalted.

Input

The first line contains integer n (1 ≤ n ≤ 50) — the number of vertical and horizontal roads in the city.

Next n2 lines contain the order of intersections in the schedule. The i-th of them contains two numbers hi, vi (1 ≤ hi, vi ≤ n), separated by a space, and meaning that the intersection that goes i-th in the timetable is at the intersection of the hi-th horizontal and vi-th vertical roads. It is guaranteed that all the intersections in the timetable are distinct.

Output

In the single line print the numbers of the days when road works will be in progress in ascending order. The days are numbered starting from 1.

Sample test(s)
input
2
1 1
1 2
2 1
2 2
output
1 4
input
1
1 1
output
1
Note

In the sample the brigade acts like that:

  1. On the first day the brigade comes to the intersection of the 1-st horizontal and the 1-st vertical road. As none of them has been asphalted, the workers asphalt the 1-st vertical and the 1-st horizontal road;
  2. On the second day the brigade of the workers comes to the intersection of the 1-st horizontal and the 2-nd vertical road. The 2-nd vertical road hasn't been asphalted, but as the 1-st horizontal road has been asphalted on the first day, the workers leave and do not asphalt anything;
  3. On the third day the brigade of the workers come to the intersection of the 2-nd horizontal and the 1-st vertical road. The 2-nd horizontal road hasn't been asphalted but as the 1-st vertical road has been asphalted on the first day, the workers leave and do not asphalt anything;
  4. On the fourth day the brigade come to the intersection formed by the intersection of the 2-nd horizontal and 2-nd vertical road. As none of them has been asphalted, the workers asphalt the 2-nd vertical and the 2-nd horizontal road.


題目大意：如果一個點的水平和豎直方向的直線都沒被訪問，則輸出點的ID

題目分析：模擬

#include <cstdio>
int const MAX = 1e4 + 5;
bool vis1[MAX], vis2[MAX];
int ans[MAX];

int main()
{
    int n, cnt = 0;
    scanf("%d", &n);
    for(int i = 0; i < n * n; i++)
    {
        int u, v;
        scanf("%d %d", &u, &v);
        if(!vis1[u] && !vis2[v])
        {
            vis1[u] = true;
            vis2[v] = true;
            ans[cnt ++] = i + 1;
        } 
    }
    for(int i = 0; i < cnt; i++)
        printf("%d ", ans[i]);
}


B. Robot's Task
time limit per test
1 second
memory limit per test
256 megabytes

Robot Doc is located in the hall, with n computers stand in a line, numbered from left to right from 1 to n. Each computer containsexactly one piece of information, each of which Doc wants to get eventually. The computers are equipped with a security system, so to crack the i-th of them, the robot needs to collect at least ai any pieces of information from the other computers. Doc can hack the computer only if he is right next to it.

The robot is assembled using modern technologies and can move along the line of computers in either of the two possible directions, but the change of direction requires a large amount of resources from Doc. Tell the minimum number of changes of direction, which the robot will have to make to collect all n parts of information if initially it is next to computer with number 1.

It is guaranteed that there exists at least one sequence of the robot's actions, which leads to the collection of all information. Initially Doc doesn't have any pieces of information.

Input

The first line contains number n (1 ≤ n ≤ 1000). The second line contains n non-negative integers a1, a2, ..., an (0 ≤ ai < n), separated by a space. It is guaranteed that there exists a way for robot to collect all pieces of the information.

Output

Print a single number — the minimum number of changes in direction that the robot will have to make in order to collect all n parts of information.

Sample test(s)
input
3
0 2 0
output
1
input
5
4 2 3 0 1
output
3
input
7
0 3 1 0 5 2 6
output
2
Note

In the first sample you can assemble all the pieces of information in the optimal manner by assembling first the piece of information in the first computer, then in the third one, then change direction and move to the second one, and then, having 2 pieces of information, collect the last piece.

In the second sample to collect all the pieces of information in the optimal manner, Doc can go to the fourth computer and get the piece of information, then go to the fifth computer with one piece and get another one, then go to the second computer in the same manner, then to the third one and finally, to the first one. Changes of direction will take place before moving from the fifth to the second computer, then from the second to the third computer, then from the third to the first computer.

In the third sample the optimal order of collecting parts from computers can look like that: 1->3->4->6->2->5->7.

題目大意：一個機器人在一條線段上收集物品，每個點有個值，只有機器人拿到的物品數大於等於點值才能拿當前點的物品，機器人從點1開始，問收集完所有的物品最少需要掉頭幾次。保證有解

題目分析：還是模擬，既然只問掉頭次數，顯然每次都走整個線段的長度是最優的，保證有解，根據題意模擬即可

#include <cstdio>
bool vis[1005];
int  a[1005];

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    int turn = 0;
    a[n + 1] = a[0] = 1005;
    for(int num = 0, dir = 1, i = 1; num < n; i += dir)
    {
        if(dir == 1 && i == n + 1)
        {
            turn ++;
            dir *= -1;
        }
        else if(dir == -1 && i == 0)
        {
            turn ++;
            dir *= -1;
        }
        if(!vis[i] && num >= a[i])
        {
            num ++;
            vis[i] = true;
        }
    }
    printf("%d\n", turn);
}

C. GCD Table
time limit per test
2 seconds
memory limit per test
256 megabytes

The GCD table G of size n × n for an array of positive integers a of length n is defined by formula

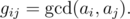
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both xand y, it is denoted as 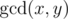. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:

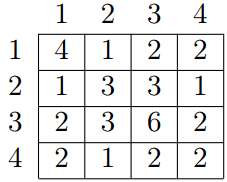
Given all the numbers of the GCD table G, restore array a.

Input

The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n2 space-separated numbers — the elements of the GCD table of G for array a.

All the numbers in the table are positive integers, not exceeding 109. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.

Output

In the single line print n positive integers — the elements of array a. If there are multiple possible solutions, you are allowed to print any of them.

Sample test(s)
input
4
2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2
output
4 3 6 2
input
1
42
output
42
input
2
1 1 1 1
output
1 1

題目大意：給n*n個GCD表裡的數字，要求按規則恢復原陣列

題目分析：顯然數字大的gcd要優先算且最大的肯定是原陣列的元素，先記錄所有數字的頻數mp[a]表示a出現了mp[a]次，也可以理解為a與別的數(包括自己)的最大公約數為a的對數有mp[a]個，然後對原陣列排序，從大數字開始記錄答案，注意記錄完要更新mp的值，比如gcd(6,2) == 2，最大公約數為2的對數要減2，因為GCD表是對稱的

#include <cstdio>
#include <algorithm>
#include <map>
int const MAX = 500 * 500 + 5;
using namespace std;
int a[MAX], ans[MAX];
map <int, int> mp;

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;  
}

int main()
{
    int n, cnt = 0;
    scanf("%d", &n);
    for(int i = 0; i < n * n; i++)
    {
        scanf("%d", &a[i]);
        mp[a[i]] ++;
    }
    sort(a, a + n * n);
    for(int i = n * n - 1; i >= 0; i--)
    {
        if(mp[a[i]] > 0)
        {
            ans[cnt ++] = a[i];
            for(int j = 0; j < cnt; j++)
                mp[gcd(a[i], ans[j])] -= 2;
        }
    }
    for(int i = 0; i < cnt - 1; i++)
        printf("%d ", ans[i]);
    printf("%d\n", ans[cnt - 1]);
}

D. Once Again...
time limit per test
1 second
memory limit per test
256 megabytes

You are given an array of positive integers a1, a2, ..., an × T of length n × T. We know that for any i > n it is true that ai = ai - n. Find the length of the longest non-decreasing sequence of the given array.

Input

The first line contains two space-separated integers: n, T (1 ≤ n ≤ 100, 1 ≤ T ≤ 107). The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 300).

Output

Print a single number — the length of a sought sequence.

Sample test(s)
input
4 3
3 1 4 2
output
5
Note

The array given in the sample looks like that: 3, 1, 4, 2, 3, 1, 4, 2, 3, 1, 4, 2. The elements in bold form the largest non-decreasing subsequence.


題目大意：把一個陣列迴圈T次，求LIS的長度

題目分析：n為100，其實對於LIS，我們只需要求n*n的即可，這裡求的是理論上長度最大的最小範圍，很好理解，一個陣列n個元素，假設我每次都只選一個來保證得到最長不減序列，那麼最多隻需要選擇n*n次，最多其實就是倒序的情況，比如 5 4 3 2 1，迴圈5次的話，第一次選1，第二次選2，以此類推。求完以後剩餘的其實只用算原陣列中頻數最大的那個即可，因為求的是最長不減序列，重複的數字可以直接插進去

#include <cstdio>
#include <algorithm>
using namespace std;
int n, T;
int a[30005], num[305];
int stk[30005];

int main() 
{
    scanf("%d %d", &n, &T);
    int ma = 0;
    for(int i = 0; i < n; i++) 
    {
        scanf("%d", &a[i]);
        num[a[i]] ++;
        ma = max(ma, num[a[i]]);
    }
    int ans = 0, len = min(100, n), top = 0;
    for(int i = n; i < n * len; i++)
        a[i] = a[i - n];
    for(int i = 0; i < n * len; i++) 
    {
        if(a[i] >= stk[top])
            stk[++ top] = a[i];
        else
        {
            int pos = upper_bound(stk, stk + top + 1, a[i]) - stk;
            stk[pos] = a[i];
        }
        ans = max(ans, top);
    }
    printf("%d\n", ans + (T - len) * ma);
}

相關文章