Codeforces Round #315 (Div. 2) (ABCD題解)

_TCgogogo_發表於2015-08-11

比賽連結：http://codeforces.com/contest/569


A. Music
time limit per test：2 seconds
memory limit per test：256 megabytes

Little Lesha loves listening to music via his smartphone. But the smartphone doesn't have much memory, so Lesha listens to his favorite songs in a well-known social network InTalk.

Unfortunately, internet is not that fast in the city of Ekaterinozavodsk and the song takes a lot of time to download. But Lesha is quite impatient. The song's duration isT seconds. Lesha downloads the first S seconds of the song and plays it. When the playback reaches the point that has not yet been downloaded, Lesha immediately plays the song from the start (the loaded part of the song stays in his phone, and the download is continued from the same place), and it happens until the song is downloaded completely and Lesha listens to it to the end. Forq seconds of real time the Internet allows you to downloadq - 1 seconds of the track.

Tell Lesha, for how many times he will start the song, including the very first start.

Input

The single line contains three integers T, S, q (2 ≤ q ≤ 104,1 ≤ S < T ≤ 105).

Output

Print a single integer — the number of times the song will be restarted.

Sample test(s)
Input
5 2 2
Output
2
Input
5 4 7
Output
1
Input
6 2 3
Output
1
Note

In the first test, the song is played twice faster than it is downloaded, which means that during four first seconds Lesha reaches the moment that has not been downloaded, and starts the song again. After another two seconds, the song is downloaded completely, and thus, Lesha starts the song twice.

In the second test, the song is almost downloaded, and Lesha will start it only once.

In the third sample test the download finishes and Lesha finishes listening at the same moment. Note that song isn't restarted in this case.


題目大意：一個人下載歌，每q個時間單位能下載q－1個時間單位的歌，歌的長度為T，下到S的時候開始播放，如果歌還沒下完且放到了還未下載的地方，則重頭開始放，問一共要放多少次


題目分析：一開始從s開始，設下了cur秒後聽和下的進度相同，則 s + (q - 1) / q * cur = cur，解得cur = q * s，然後從頭開始，設t'秒後進度相同，則(q - 1) / q * t' + cur = t'，解得t' = cur * q，可見直接拿第一次進度相同的時間乘q就是接下來每次進度相同的時間


#include <cstdio>

int main()
{
    int T, S, q, ans = 1, cur;
    scanf("%d %d %d", &T, &S, &q);
    cur = q * S;
    while(cur < T)
    {
        cur = q * cur;
        ans ++;
    }
    printf("%d\n", ans);
}


B. Inventory
time limit per test：1 second
memory limit per test：256 megabytes

Companies always have a lot of equipment, furniture and other things. All of them should be tracked. To do this, there is an inventory number assigned with each item. It is much easier to create a database by using those numbers and keep the track of everything.

During an audit, you were surprised to find out that the items are not numbered sequentially, and some items even share the same inventory number! There is an urgent need to fix it. You have chosen to make the numbers of the items sequential, starting with 1. Changing a number is quite a time-consuming process, and you would like to make maximum use of the current numbering.

You have been given information on current inventory numbers forn items in the company. Renumber items so that their inventory numbers form apermutation of numbers from 1 to n by changing the number of as few items as possible. Let us remind you that a set ofn numbers forms a permutation if all the numbers are in the range from 1 to n, and no two numbers are equal.

Input

The first line contains a single integer n — the number of items (1 ≤ n ≤ 105).

The second line contains n numbersa1, a2, ..., an (1 ≤ ai ≤ 105) — the initial inventory numbers of the items.

Output

Print n numbers — the final inventory numbers of the items in the order they occur in the input. If there are multiple possible answers, you may print any of them.

Sample test(s)
Input
3
1 3 2
Output
1 3 2
Input
4
2 2 3 3
Output
2 1 3 4
Input
1
2
Output
1
Note

In the first test the numeration is already a permutation, so there is no need to change anything.

In the second test there are two pairs of equal numbers, in each pair you need to replace one number.

In the third test you need to replace 2 by 1, as the numbering should start from one.


題目大意：給n個數，可以改變任意個數字的大小目標是將其改成1-n的一個排列，要求改變次數最小，輸出排列


題目分析：記錄原始序列已經在1-n位置的數，凡是大於n的或者重複出現的數字下標 標記一下，列舉一下1-n中還有哪些數字沒出現，然後按順序修改

#include <cstdio>
#include <cstring>
int const MAX = 1e5 + 5;
int a[MAX], need[MAX];
bool has[MAX], pos[MAX];

int main()
{
    int n, num = 0;
    scanf("%d", &n);
    memset(has, false, sizeof(has));
    memset(pos, false, sizeof(pos));
    for(int i = 0; i < n; i++)
    {
        scanf("%d", &a[i]);
        if(!has[a[i]] && a[i] <= n)
            has[a[i]] = true;
        else
            pos[i] = true;
    }
    int cnt = 0;
    for(int i = 1; i <= n; i++)
        if(!has[i])
            need[cnt ++] = i;
    int idx = 0;
    for(int i = 0; i < n; i++)
        if(pos[i])
            a[i] = need[idx ++];
    for(int i = 0; i < n - 1; i++)
        printf("%d ", a[i]);
    printf("%d\n", a[n - 1]);
}



C. Primes or Palindromes?
time limit per test：3 seconds
memory limit per test：256 megabytes

Rikhail Mubinchik believes that the current definition of prime numbers is obsolete as they are too complex and unpredictable. A palindromic number is another matter. It is aesthetically pleasing, and it has a number of remarkable properties. Help Rikhail to convince the scientific community in this!

Let us remind you that a number is called prime if it is integer larger than one, and is not divisible by any positive integer other than itself and one.

Rikhail calls a number a palindromic if it is integer, positive, and its decimal representation without leading zeros is a palindrome, i.e. reads the same from left to right and right to left.

One problem with prime numbers is that there are too many of them. Let's introduce the following notation:π(n) — the number of primes no larger thann, rub(n) — the number of palindromic numbers no larger thann. Rikhail wants to prove that there are a lot more primes than palindromic ones.

He asked you to solve the following problem: for a given value of the coefficientA find the maximum n, such that π(n) ≤ A·rub(n).

Input

The input consists of two positive integers p, q, the numerator and denominator of the fraction that is the value ofA (, ).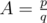

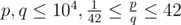Output

If such maximum number exists, then print it. Otherwise, print"Palindromic tree is better than splay tree" (without the quotes).

Sample test(s)
Input
1 1
Output
40
Input
1 42
Output
1
Input
6 4
Output
172


題目大意：π(n) 為不大於n的素數個數，rub(n)為不大於n的迴文數個數，A=p/q，現在要求最大的n，使得π(n) ≤ A·rub(n)

題目分析：預處理這兩類數的個數，陣列儘量往大了開吧，1e7過了

#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long  
using namespace std;
int const MAX = 1e7 + 5;
int cntpr[MAX], cntpa[MAX], p[MAX];
bool prime[MAX];

void get_prime()
{
    int pnum = 1;
    memset(cntpr, 0, sizeof(cntpr));
    memset(prime, true, sizeof(prime));
    for(int i = 2; i <= MAX; i++)
    {
        cntpr[i] = cntpr[i - 1];
        if(prime[i])
        {
            cntpr[i] ++;
            p[pnum ++] = i;
        }
        for(int j = 1; j <= pnum && i * p[j] < MAX; j++)
        {
            prime[i * p[j]] = false;
            if(i % p[j] == 0)
                break;
        }
    }
}

bool judge(int x)
{
    char s[10];
    sprintf(s, "%d", x);
    int len = strlen(s);
    for(int i = 0; i < len / 2; i++)
        if(s[i] != s[len - i - 1])
            return false;
    return true;
}

void get_palindromes()
{
    memset(cntpa, 0, sizeof(cntpa));
    for(int i = 1; i <= MAX; i++)
    {
        cntpa[i] = cntpa[i - 1];
        if(judge(i))
            cntpa[i] ++;
    }
}

int main()
{
    bool flag = false;
    int p, q;
    int ans = 0;
    get_prime();
    get_palindromes();
    scanf("%d %d", &p, &q);
    for(int i = 1; i <= MAX; i++)
    {
        if((ll) q * cntpr[i] <= (ll) p * cntpa[i])
        {
            ans = max(ans, i);
            flag = true;
        }
    }
    if(flag)
        printf("%d\n", ans);
    else
        printf("Palindromic tree is better than splay tree\n");
}



D. Symmetric and Transitive
time limit per test：1.5 seconds
memory limit per test：256 megabytes

Little Johnny has recently learned about set theory. Now he is studying binary relations. You've probably heard the term "equivalence relation". These relations are very important in many areas of mathematics. For example, the equality of the two numbers is an equivalence relation.

A set ρ of pairs (a, b) of elements of some setA is called a binary relation on set A. For two elements a and b of the set A we say that they are in relationρ, if pair 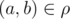, in this case we use a notation.

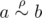Binary relation is equivalence relation, if:

  1. It is reflexive (for any a it is true that);
  2. It is symmetric (for any a, b it is true that if 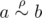, then);
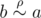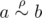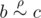  3. It is transitive (if and, than).

Little Johnny is not completely a fool and he noticed that the first condition is not necessary! Here is his "proof":

Take any two elements, a and b. If 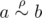, then 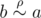(according to property (2)), which means (according to property (3)).

It's very simple, isn't it? However, you noticed that Johnny's "proof" is wrong, and decided to show him a lot of examples that prove him wrong.

Here's your task: count the number of binary relations over a set of size n such that they are symmetric, transitive, but not an equivalence relations (i.e. they are not reflexive).

Since their number may be very large (not 0, according to Little Johnny), print the remainder of integer division of this number by109 + 7.

Input

A single line contains a single integer n(1 ≤ n ≤ 4000).

Output

In a single line print the answer to the problem modulo 109 + 7.

Sample test(s)
Input
1
Output
1
Input
2
Output
3
Input
3
Output
10
Note

If n = 1 there is only one such relation — an empty one, i.e.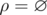. In other words, for a single elementx of set A the following is hold:.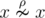

If n = 2 there are three such relations. Let's assume that setA consists of two elements, x and y. Then the valid relations are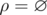,ρ = {(x, x)}, ρ = {(y, y)}. It is easy to see that the three listed binary relations are symmetric and transitive relations, but they are not equivalence relations.


題目大意：學過離散數學的同學理解起題意更快，求1到n，n個元素組成的集合中，滿足對稱性和傳遞性但不滿足自反性的二元組關係集合的個數

題目分析：先結束下樣例3，可以是
空集
{<a, a>}， {<b, b>}，{<c, c>}
{<a, a>, <b, b>}，{<a, a>, <c, c>}，{<b, b>, <c, c>}
{<a, a>, <b, b>, <a, b>, <b, a>}，{<b, b>, <c, c>, <b, c>, <c, b>}，{<a, a>, <c, c>, <a, c>, <c, a>} 一共10個
因為每組等價關係的個數正好等於Bell數，所以不難推出ans[i] = Bell[i + 1] - Bell[i]，從下一個等價關係個數中減去從當前等價關係推出的個數即為當前不滿足自反的二元組關係個數，直接推Bell三角形即可

#include <cstdio>
#define ll long long
int const MAX = 4005;
int const MOD = 1e9 + 7;
ll dp[MAX][MAX];

int main()
{
    int n;
    scanf("%d", &n);
    dp[0][0] = 1;
    for(int i = 1; i <= n; i++)
    {
        dp[i][0] = dp[i - 1][i - 1];
        for(int j = 1; j <= i; j++)
            dp[i][j] = (dp[i][j - 1] + dp[i - 1][j - 1]) % MOD;
    }
    printf("%I64d\n", dp[n][n - 1]);
}





相關文章