Codeforces Round #313 (Div. 2) (ABCDE題解)
比賽連結:http://codeforces.com/contest/560
A magic island Geraldion, where Gerald lives, has its own currency system. It uses banknotes of several values. But the problem is, the system is not perfect and sometimes it happens that Geraldionians cannot express a certain sum of money with any set of banknotes. Of course, they can use any number of banknotes of each value. Such sum is calledunfortunate. Gerald wondered: what is the minimumunfortunate sum?
The first line contains number n (1 ≤ n ≤ 1000) — the number of values of the banknotes that used in Geraldion.
The second line contains n distinct space-separated numbersa1, a2, ..., an (1 ≤ ai ≤ 106) — the values of the banknotes.
Print a single line — the minimum unfortunate sum. If there are no unfortunate sums, print - 1.
5
1 2 3 4 5
-1
題目大意:n種紙幣每個面值為ai,問最小的不能組成的面值大小
題目分析:有1輸-1,沒1輸1
#include <cstdio>
int main()
{
int ans = 1, n;
scanf("%d", &n);
for(int i = 0; i < n; i++)
{
int get;
scanf("%d", &get);
if(get == 1)
ans = -1;
}
printf("%d\n", ans);
}Gerald bought two very rare paintings at the Sotheby's auction and he now wants to hang them on the wall. For that he bought a special board to attach it to the wall and place the paintings on the board. The board has shape of an a1 × b1 rectangle, the paintings have shape of aa2 × b2 anda3 × b3 rectangles.
Since the paintings are painted in the style of abstract art, it does not matter exactly how they will be rotated, but still, one side of both the board, and each of the paintings must be parallel to the floor. The paintings can touch each other and the edges of the board, but can not overlap or go beyond the edge of the board. Gerald asks whether it is possible to place the paintings on the board, or is the board he bought not large enough?
The first line contains two space-separated numbersa1 andb1 — the sides of the board. Next two lines contain numbersa2, b2, a3 andb3 — the sides of the paintings. All numbersai, bi in the input are integers and fit into the range from1 to1000.
If the paintings can be placed on the wall, print "YES" (without the quotes), and if they cannot, print "NO" (without the quotes).
3 2
1 3
2 1
YES
5 5
3 3
3 3
NO
4 2
2 3
1 2
YES
That's how we can place the pictures in the first test:

And that's how we can do it in the third one.
題目大意:三個矩形,給出邊長,問後兩個能不能放到第一個裡
題目分析:懶得說,就那麼點情況而已
#include <cstdio>
#include <algorithm>
using namespace std;
int a1, a2, a3, b1, b2, b3;
bool J(int x, int y)
{
return (x <= a1 && y <= b1 || x <= b1 && y <= a1);
}
int main()
{
scanf("%d %d %d %d %d %d", &a1, &b1, &a2, &b2, &a3, &b3);
if(J(a2 + a3, max(b2, b3))
|| J(b2 + b3, max(a2, a3))
|| J(a2 + b3, max(b2, a3))
|| J(a3 + b2, max(b3, a2)))
printf("YES\n");
else
printf("NO\n");
}Gerald got a very curious hexagon for his birthday. The boy found out that all the angles of the hexagon are equal to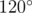 .
Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.
.
Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters. There the properties of the hexagon ended and Gerald decided to draw on it.
He painted a few lines, parallel to the sides of the hexagon. The lines split the hexagon into regular triangles with sides of 1 centimeter. Now Gerald wonders how many triangles he has got. But there were so many of them that Gerald lost the track of his counting. Help the boy count the triangles.
The first and the single line of the input contains 6 space-separated integersa1, a2, a3, a4, a5 anda6 (1 ≤ ai ≤ 1000) — the lengths of the sides of the hexagons in centimeters in the clockwise order. It is guaranteed that the hexagon with the indicated properties and the exactly such sides exists.
Print a single integer — the number of triangles with the sides of one 1 centimeter, into which the hexagon is split.
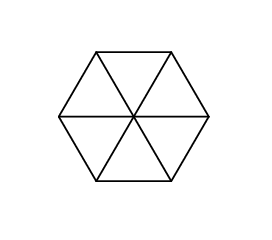
1 1 1 1 1 1
6
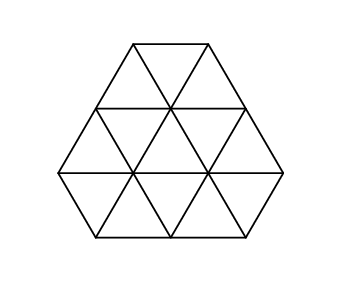
1 2 1 2 1 2
13
This is what Gerald's hexagon looks like in the first sample:
And that's what it looks like in the second sample:
題目大意:給出六邊形6個邊長,求裡面有多少個邊長為1的正三角形
題目分析:這題還有點意思,把它補成大正三角形,大正三角形包含的小三角個數為邊長^2,等差數列求和,因為邊按順序給的,通過旋轉我們可以發現大邊長等於a1+a2+a3,多出來的另外三個正三角形的邊長為a1,a3,a5,所以最後答案就是(a1+a2+a3)^2-a1^2-a3^2-a5^2
#include <cstdio>
#include <cstring>
int const MAX = 3005;
int fac[MAX];
int main()
{
for(int i = 1; i <= MAX; i++)
fac[i] = i * i;
int a[7];
for(int i = 1; i <= 6; i++)
scanf("%d", &a[i]);
printf("%d\n", fac[a[1] + a[2] + a[3]] - fac[a[1]] - fac[a[3]] - fac[a[5]]);
}
Today on a lecture about strings Gerald learned a new definition of string equivalency. Two stringsa andb of equal length are calledequivalent in one of the two cases:
- They are equal.
- If we split string a into two halves of the same sizea1 anda2,
and stringb into two halves of the same sizeb1 andb2, then one of the following
is correct:
- a1 is equivalent tob1, anda2 is equivalent tob2
- a1 is equivalent tob2, anda2 is equivalent tob1
As a home task, the teacher gave two strings to his students and asked to determine if they are equivalent.
Gerald has already completed this home task. Now it's your turn!
The first two lines of the input contain two strings given by the teacher. Each of them has the length from1 to200 000 and consists of lowercase English letters. The strings have the same length.
Print "YES" (without the quotes), if these two strings are equivalent, and "NO" (without the quotes) otherwise.
aaba
abaa
YES
aabb
abab
NO
In the first sample you should split the first string into strings "aa" and "ba", the second one — into strings "ab" and "aa". "aa" is equivalent to "aa"; "ab" is equivalent to "ba" as "ab" = "a" + "b", "ba" = "b" + "a".
In the second sample the first string can be splitted into strings "aa" and "bb", that are equivalent only to themselves. That's why string "aabb" is equivalent only to itself and to string "bbaa".
題目大意:給兩個字串,判斷它們是否相等,相等有兩種情況,一個是直接相等,一個是切成長度相同的兩份以後兩子串交叉相等
題目分析:裸的DFS,按照題意搜就行了,如果當前長度為奇數,直接返回false,否則分兩種情況搜
這題是水過的,兩種情況位置調換T91。。。orz,神人品,不過把string改成char*,怎麼都可以過
#include <cstdio>
#include <cstring>
int const MAX = 250000;
char a[MAX], b[MAX];
bool DFS(char *p1, char *p2, int len)
{
if(!strncmp(p1, p2, len))
return true;
if(len % 2)
return false;
int n = len / 2;
if(DFS(p1 ,p2 + n, n) && DFS(p1 + n, p2, n))
return true;
if(DFS(p1, p2, n) && DFS(p1 + n, p2 + n, n))
return true;
return false;
}
int main()
{
scanf("%s %s", a, b);
printf("%s\n", DFS(a, b, strlen(a)) ? "YES" : "NO");
}
Giant chess is quite common in Geraldion. We will not delve into the rules of the game, we'll just say that the game takes place on anh × w field, and it is painted in two colors, but not like in chess. Almost all cells of the field are white and only some of them are black. Currently Gerald is finishing a game of giant chess against his friend Pollard. Gerald has almost won, and the only thing he needs to win is to bring the pawn from the upper left corner of the board, where it is now standing, to the lower right corner. Gerald is so confident of victory that he became interested, in how many ways can he win?
The pawn, which Gerald has got left can go in two ways: one cell down or one cell to the right. In addition, it can not go to the black cells, otherwise the Gerald still loses. There are no other pawns or pieces left on the field, so that, according to the rules of giant chess Gerald moves his pawn until the game is over, and Pollard is just watching this process.
The first line of the input contains three integers:h, w, n — the sides of the board and the number of black cells (1 ≤ h, w ≤ 105, 1 ≤ n ≤ 2000).
Next n lines contain the description of black cells. Thei-th of these lines contains numbersri, ci (1 ≤ ri ≤ h, 1 ≤ ci ≤ w) — the number of the row and column of the i-th cell.
It is guaranteed that the upper left and lower right cell are white and all cells in the description are distinct.
Print a single line — the remainder of the number of ways to move Gerald's pawn from the upper left to the lower right corner modulo109 + 7.
3 4 2
2 2
2 3
2
100 100 3
15 16
16 15
99 88
545732279
題目大意:一個矩形,從右上到左下在有n個點不能路過的情況下有幾種走法
題目分析:因為h,w比較大,不能開二維,可是n很小,我們從n入手,考慮到每個點不經過壞點有多少種走法,先對點按x優先的從小到大排序
dp[i] = C(xi - 1 + yi - 1, xi - 1)這是從原點到點xi,yi的方案數,因為往右最多走xi-1步,往下最多走yi-1步,因此總共走了xi -1 + yi - 1步,所以走的可能情況直接算組合數,其實xi,yi處是壞點,先假定能在壞點上,然後我們要減去之前遇到的壞點,直接列舉在xi,yi之前的點,那麼兩個壞點間的走法是C(xi - xj + yi - yj,xi - xj)種,拿dp[i] - Σdp[j],即把到xi,yi經過之前壞點的情況去掉了,注意我們要把終點加到座標集合中,這樣最後到終點時就把所有經過壞點的可能情況都減去了,不妨畫個圖理解理解,另外這題的要用到組合數取模,要求逆元,板子不好直接導致T20,換了2份板子才過。。。
#include <cstdio>
#include <algorithm>
using namespace std;
#define ll long long
int const MOD = 1e9 + 7;
ll fac[200005], dp[2005], inv[200005];
int h, w, n;
struct Point
{
int x, y;
}p[2005];
bool cmp(Point a, Point b)
{
if(a.x == b.x)
return a.y < b.y;
return a.x < b.x;
}
ll get_inv(ll x)
{
ll res = 1, y = MOD - 2;
while(y)
{
if(y & 1)
res = (res * x) % MOD;
x = (x * x) % MOD;
y >>= 1;
}
return res;
}
void pre()
{
fac[0] = 1;
inv[0] = 1;
for(int i = 1; i <= 200005; i++)
{
fac[i] = (fac[i - 1] * i) % MOD;
inv[i] = get_inv(fac[i]);
}
}
ll C(int n, int m)
{
return fac[n] * inv[m] % MOD * inv[n - m]% MOD;
}
int main()
{
pre();
scanf("%d %d %d", &h, &w, &n);
for(int i = 1; i <= n; i++)
scanf("%d %d", &p[i].x, &p[i].y);
p[++ n].x = h;
p[n].y = w;
sort(p + 1, p + n + 1, cmp);
for(int i = 1; i <= n; i++)
{
dp[i] = C(p[i].x + p[i].y - 2, p[i].x - 1);
for(int j = 1; j < i; j++)
if(p[j].x <= p[i].x && p[j].y <= p[i].y)
dp[i] = (dp[i] % MOD + MOD - dp[j] * C(p[i].x - p[j].x + p[i].y - p[j].y, p[i].x - p[j].x) % MOD) % MOD;
}
printf("%lld\n", dp[n]);
}相關文章
- Codeforces Round #186 (Div. 2) (ABCDE題解)
- Codeforces Round #105 (Div. 2) (ABCDE題解)
- Codeforces Round #200 (Div. 2) (ABCDE題解)
- Codeforces Round #320 (Div. 2) [Bayan Thanks-Round] (ABCDE題解)
- Codeforces Round 976 (Div. 2) 題解
- Codeforces Round 983 (Div. 2) 題解
- Codeforces Round #956 (Div. 2)題解
- Codeforces Round 951 (Div. 2) 題解
- Codeforces Round 965 (Div. 2) 題解
- Codeforces Round #681 (Div. 2)E題解
- Codeforces Round 932 (Div. 2) DE 題解
- Educational Codeforces Round 93 (Rated for Div. 2)題解
- Codeforces Round #665 (Div. 2)A-C題解
- Codeforces Round #673 (Div. 2)(A-D)題解
- Codeforces Round #439 (Div. 2) A-C題解
- Codeforces Round #Pi (Div. 2) (ABCD題解)
- Codeforces Round 976 (Div. 2) 題解(A-E)
- Codeforces Round 893 (Div. 2)題解記錄
- Codeforces Round 892 (Div. 2)題解記錄
- Educational Codeforces Round 171 (Rated for Div. 2) 題解
- Codeforces Round #313 (Div. 2) 560C Gerald's Hexagon(腦洞)Go
- Codeforces Round #537 (Div. 2)解題報告
- Codeforces Round #266 (Div. 2)解題報告
- Codeforces Round #323 (Div. 2) (ABCD題解)
- Codeforces Round #331 (Div. 2) (ABC題解)
- Codeforces Round 899 (Div. 2)題解記錄
- Codeforces Round 979 (Div. 2) (ABCD個人題解)
- Educational Codeforces Round 168 (Rated for Div. 2) 題解
- Codeforces Round 986 (Div. 2)題解記錄(A~D)
- Codeforces Round 987 (Div. 2)題解記錄(A~D)
- Codeforces Round 984 (Div. 3) 題解
- Codeforces Round 962 (Div. 3) 題解
- Codeforces Round 946 (Div. 3) 題解
- Codeforces Round #646 (Div. 2)【C. Game On Leaves 題解】GAM
- Codeforces Round #319 (Div. 2) (ABCE題解)
- Codeforces Round #315 (Div. 2) (ABCD題解)
- Codeforces Round 975 (Div. 2)題解記錄(A,B,E)
- Codeforces Round #639 (Div. 2)