Generalizing RDP Codes Using the Combinatorial Method

#摘要
本文提出了PDHLatin，它是一種基於列漢密爾頓拉丁方(CHIS-column hamiltonian Latin squares)構造的校驗塊獨立的2容錯水平碼。通過證明它是MDS碼。 本文也提出了一種新的基於CHIS的校驗塊獨立的2容錯混合編碼-PIMLatin。 這兩種編碼具有良好的擴充套件性以及結構多樣性。 同時本文也討論編碼縮減技術，以及它所帶來的引數擴充套件性，結構可變性和可靠性的提升。 基於垂直縮減的思想，本文利用非漢密爾頓拉丁方的方式提出了一種2容錯陣列碼的構建方式。

#簡介
磁碟容量的增大，以及儲存系統規模的增大導致多故障頻發。 因此，多容錯糾刪碼變得流行起來，但是當前的多容錯糾刪碼具有一些內在的侷限性。Plank在Fast05上tutorial對儲存系統的糾刪碼給出了一個詳細的介紹。糾刪碼是一種編碼容錯機制。 它將$n$個資料磁碟編碼成$m$個校驗磁碟，並且可以容錯任意的$t$個磁碟的故障，但是並沒有一種針對$n$, $m$,$t$>$1$情況下的一致公認的最優編碼技術。

廣為人知的多容錯編碼技術主要分為三種類別： Reed-Solomon碼， 二進位制線性碼和陣列碼。

1. RS碼是僅有的一種適用於任意$n$, $m$(=$t$)MDS碼。 這意味著最優的儲存效率以及更新效率。 但是由於它使用Galois Field進行編解碼運算(雖然一些優化的方法提出來)，計算複雜性是一個很嚴重的問題。
2. 二進位制線性碼是基於XOR的編碼，具有較優的計算複雜性，但是儲存效率比較低。 圖1展示了一種2維線性碼，其中資料單元$D_{ij}$同時參與了兩個校驗塊$P_i$和$Q_i$的計算。 這個例子說明了線性碼的核心觀點： 將資料單元分配到多個校驗組中，也就是說一個資料單元參與到多個組，保證了多容錯特性。
3. 陣列碼將資料或者校驗單元組織到一個array中。 EVENODD是第一種MDS陣列碼，其他隨後的一些陣列碼像X-COde, RDP, STAR-code等都與它有思想上相似的地方。

#圖論知識
又找了一篇相關的論文：Combinatorial Constructions of Multi-Erasure-Correcting Codes with
Independent Parity Symbols for Storage Systems 依然卡在了P1F以及拉丁方上，因此著眼於這些知識的理論搭建。

##P1F相關
所謂一個圖G的因子Gi，是指至少包含G的一條邊的生成子圖。
所謂一個圖G的因子分解，是指把圖G分解為若干個邊不重的因子之並。
所謂一個圖G的n因子，是指圖G的n度正則因子。
生成子圖： 與圖G的頂點相同，邊是子集。
正則圖： 圖的所有頂點的度都相同，例如孤立的一群點是0-度正則圖
n度正則因子： 首先得滿足因子$G_i$，然後滿足正則的概念。

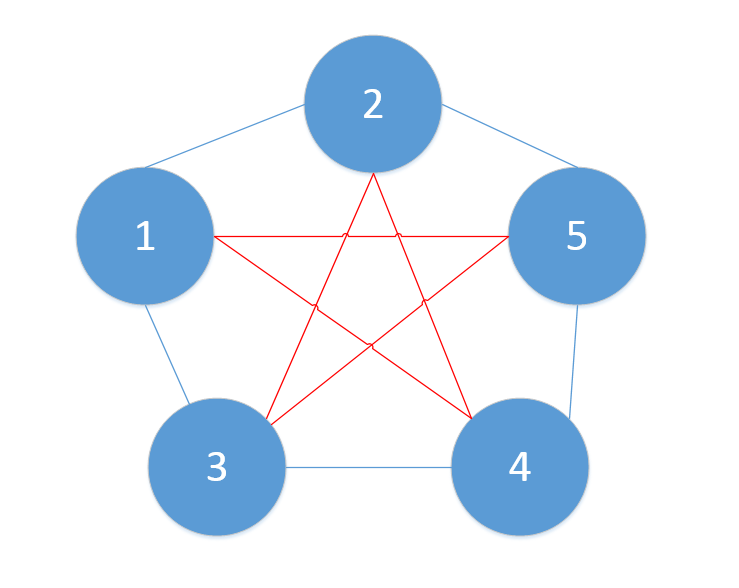
例如這個五邊形內部的紅色五角形就是圖的一個2因子。

匹配： 圖的一個匹配是圖的一些邊的集合，這些邊沒有公共的頂點。
最大匹配： 首先是圖的一個匹配，然後邊的數目最多
完美匹配： 是圖的一個匹配，且能囊括所有的頂點。
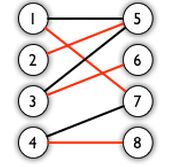
例如，下圖就是一個完美匹配

圖的一因子分解：圖可以分解為若干個邊不重複的完美匹配的匯出子圖。
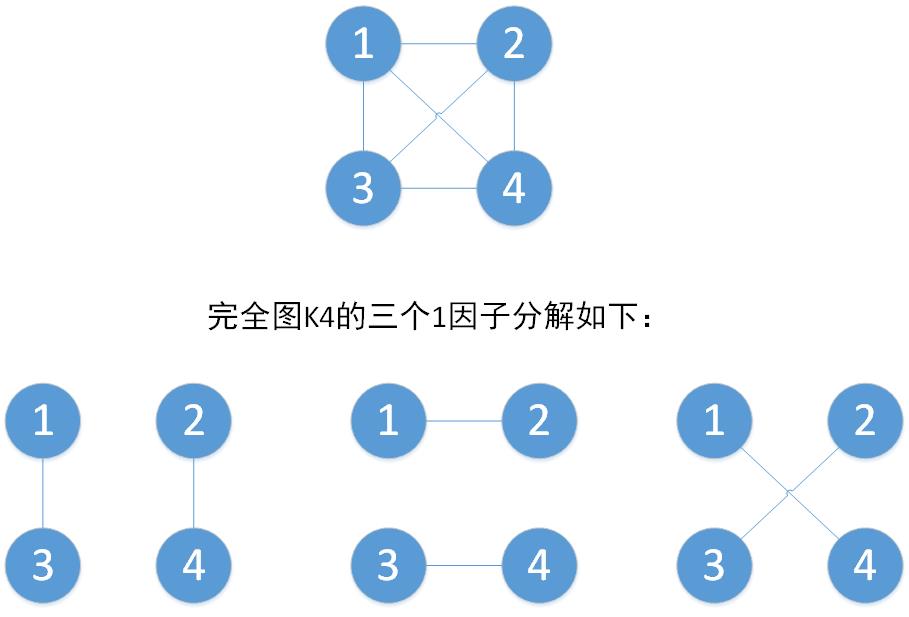
例如具有$2n$個頂點的完全圖$K_{2n}$可進行一因子分解，$K_4$可分解為3個1因子。

完美1因子分解： 如果一個圖可以進行一因子分解，且對於任意的兩個因子$F_i$和$F_j$，有$F_i U F_j$產生了漢密爾頓迴路，那麼這種1因子分解就是完美1因子分解，簡寫為P1F。
漢密爾頓迴路： $n$個頂點，$n$條邊組成了一個環路，這樣的環路只要刪除其中任意一條邊就不會再有迴路，這種環路叫做漢密爾頓迴路。 通過圖G的每個結點一次，且僅一次的通路（迴路）。
具有偶數個節點的完全圖都有P1F。

##拉丁方相關
對於$k \leq n$，一個$k*n$的拉丁矩陣是1個$k*n$的矩陣，而且矩陣的每一行和每一列都沒有重複的元素。 通常我們使用$Z_n = {0, 1, \cdots, n-1}$作為元素集合，用$L(k,n)$叫做$k*n$的拉丁矩陣，$L(k,n)$中的第$r$行，第$c$列的元素是$R_{rc}$。 我們稱$L(n,n)$叫做拉丁方陣，且可以使用具有$n^2$個條目的$3$元組$(row, column, symbol)$來表示它。

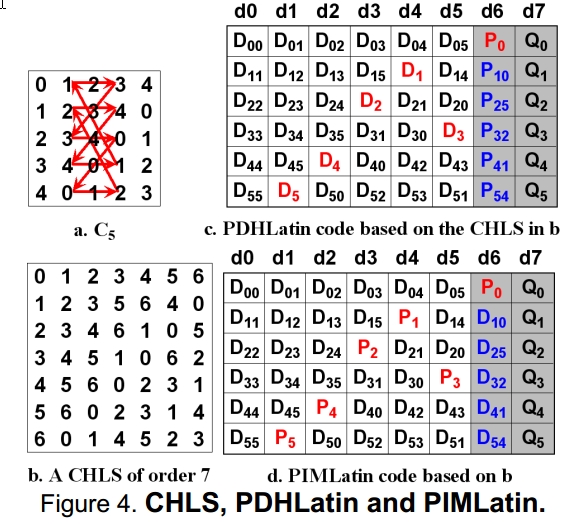
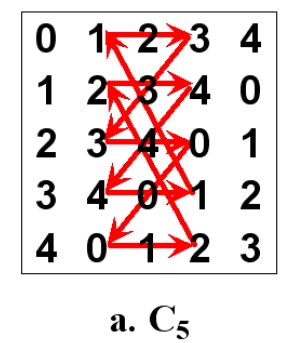
拉丁矩陣$R$的每一行都是上述$Z_n$的一個排列。如果拉丁方$L$的兩行組成一個單一的環，那麼$L$叫做行漢密爾頓拉丁方，本文關注列漢密爾頓拉丁方(CHIS)，也就是兩列組成一個環，如下圖的$C_5$。

###CHIS和P1F的相互轉換
CHIS和P1F具有緊密的聯絡。n階CHIS可以轉換為一個P1F(V, W, E)，過程如下：使頂點$V =\{ v_i | 0\leq i \leq n-1\}$，使頂點$W =\{ w_i | 0\leq i \leq n-1\}$，對於所有的$(i,j,k) \in L$， 使邊$(v_i, w_k) \in F_j $， 同樣這個過程也可以反向進行。

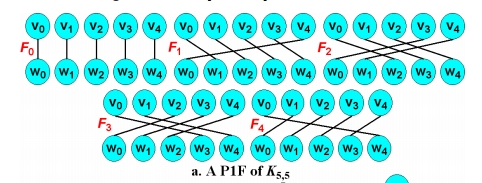
如下圖的例子，P1F和CHIS一一對應：


轉換過程
首先由$K_{5,5}$生成一個完美1因子匹配(即每一個子圖的頂點的度都是1)，每一對因子$F_i$, $F_j$都可以形成漢密爾頓環路。 下面的是一個5階列漢密爾頓拉丁方。 這兩個圖可以相互轉換($C_5 和 K_{5,5}$)。
將P1F中的$F_j$對應於$C_5$的第j列；將$C_5$第$j$列的元素的行號$i$作為$F_j$中V頂點的下標， 即$v_i$； 將$C_5$第$j$列的元素的值$k$作為$F_j$中W頂點的下標， 即$w_k$。 舉例說明： j=1，對應於$K_{5,5}$的$F_1$和$C_5$的第1列，即$1,2,3,4,0$； 在$C_5$中，當$i=0$時，$k=1$(第$0$行，第$1$列的元素值為$1$)，因此在$F_1$中$v_0$與$w_1$相連， 同樣當$i=1$時，$k=2$(第$1$行，第$1$列的元素值為$2$)，因此$F_1$中$v_1$與$w_2$相連。

對於$C_5$中的第1,3列形成環路，其實就是說對於$K_{5,5}$中的P1F， $F_1$和$F_3$形成了環路，這兩個是等價的。

如果$K_{n+1}$具有P1F，$K_{n,n}$也具有，由於已知偶數節點的完全圖具有完美1因子，因此當n為奇數(n=2也可以)時，$K_{n,n}$ 具有P1F。

#新的編碼
#PDHLatin codes

#未完待續