機器學習-決策樹

jiangjiane發表於2017-08-21
機器學習

決策樹（decision tree）

轉載自：點選開啟連結

說明：這篇部落格是看周志華老師的《機器學習》（西瓜書）的筆記總結，雖然自己寫了很多總結性文字包括一些演算法細節，但部落格中仍有部分文字摘自周老師的《機器學習》書，僅供學習交流使用。轉載部落格務必註明出處和作者，謝謝。

        決策樹演算法起源於E.B.Hunt等人於1966年發表的論文“experiments in Induction”，但真正讓決策樹成為機器學習主流演算法的還是Quinlan（羅斯.昆蘭）大神（2011年獲得了資料探勘領域最高獎KDD創新獎），昆蘭在1979年提出了ID3演算法，掀起了決策樹研究的高潮。現在最常用的決策樹演算法是C4.5是昆蘭在1993年提出的。（關於為什麼叫C4.5，還有個軼事：因為昆蘭提出ID3後，掀起了決策樹研究的高潮，然後ID4，ID5等名字就被佔用了，因此昆蘭只好讓講自己對ID3的改進叫做C4.0，C4.5是C4.0的改進）。現在有了商業應用新版本是C5.0link。
一、決策樹的基本概念
        顧名思義，決策樹就是一棵樹，一顆決策樹包含一個根節點、若干個內部結點和若干個葉結點；葉結點對應於決策結果，其他每個結點則對應於一個屬性測試；每個結點包含的樣本集合根據屬性測試的結果被劃分到子結點中；根結點包含樣本全集，從根結點到每個葉子結點的路徑對應了一個判定測試序列。下面直接上個圖，讓大家看下決策樹是怎樣決策的（以二元分類為例），圖中紅線表示給定一個樣例（表中資料）決策樹的決策過程：


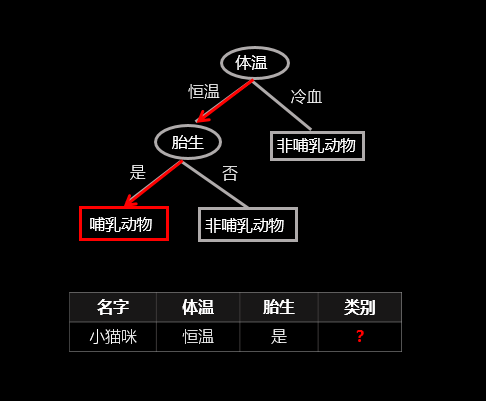
（該圖為原創）

二、如何生成決策樹
  • 資訊增益
        決策樹學習的關鍵在於如何選擇最優的劃分屬性，所謂的最優劃分屬性，對於二元分類而言，就是儘量使劃分的樣本屬於同一類別，即“純度”最高的屬性。那麼如何來度量特徵（features）的純度，這時候就要用到“資訊熵（information entropy）”。先來看看資訊熵的定義：假如當前樣本集D中第k類樣本所佔的比例為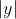，為類別的總數（對於二元分類來說，）。則樣本集的資訊熵為：

的值越小，則D的純度越高。再來看一個概念資訊增益（information gain），假定離散屬性有V個可能的取值，如果使用特徵來對資料集D進行劃分，則會產生V個分支結點， 其中第v（小v）個結點包含了資料集D中所有在特徵上取值為的樣本總數，記為。因此可以根據上面資訊熵的公式計算出資訊熵，再考慮到不同的分支結點所包含的樣本數量不同，給分支節點賦予權重，從這個公式能夠發現包含的樣本數越多的分支結點的影響越大（這樣是資訊增益的一個缺點，即資訊增益對可取值數目多的特徵有偏好（即該屬效能取得值越多，資訊增益，越偏向這個），待會後面會舉例子說明，這個缺點可以用資訊增益率來解決）。因此，能夠計算出特徵對樣本集D進行劃分所獲得的“資訊增益”:

       一般而言，資訊增益越大，則表示使用特徵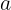對資料集劃分所獲得的“純度提升”越大。所以資訊增益可以用於決策樹劃分屬性的選擇，其實就是選擇資訊增益最大的屬性，ID3演算法就是採用的資訊增益來劃分屬性。
下面來舉個例子說明具體是怎樣操作的，只貼公式沒多大意義，還是有不利於大家理解。舉例子用的資料集為：

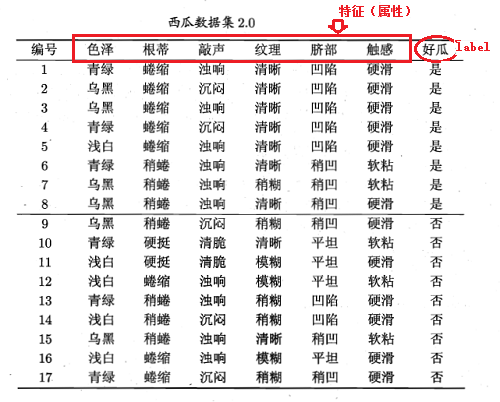
    顯然該資料集包含17個樣本，類別為二元的，即。則，正例（類別為1的樣本）佔的比例為：，反例（類別為0的樣本）佔的比例為：。根據資訊熵的公式能夠計算出資料集D的資訊熵為：
從資料集中能夠看出特徵集為：{色澤、根蒂、敲聲、紋理、臍部、觸感}。下面我們來計算每個特徵的資訊增益。先看“色澤”，它有三個可能的離散取值：{青綠、烏黑、淺白}，若使用“色澤”對資料集D進行劃分，則可得到3個子集，分別為：（色澤=青綠）、（色澤=烏黑）、（色澤=淺白）。共包含6個樣本，其中正例佔，反例佔。包含6個樣本，其中正例佔，反例佔。包含了5個樣本，其中正例佔
，反例佔。因此，可以計算出用“色澤”劃分之後所獲得的3個分支結點的資訊熵為：


因此，特徵“色澤”的資訊增益為：


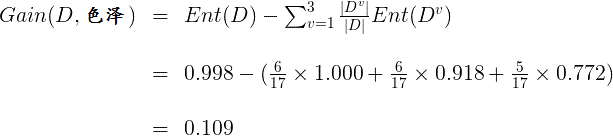
同理可以計算出其他特徵的資訊增益：

比較發現，特徵“紋理”的資訊增益最大，於是它被選為劃分屬性。因此可得：

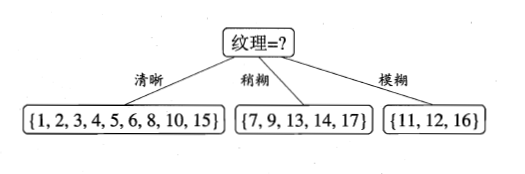
第二步、繼續對上圖中每個分支進行劃分，以上圖中第一個分支結點{“紋理=清晰”}為例，對這個結點進行劃分，設該結點的樣本集，共9個樣本，可用特徵集合為{色澤，根蒂，敲聲，臍部，觸感}，因此基於能夠計算出各個特徵的資訊增益：

比較發現，“根蒂”、“臍部”、“觸感”這3個屬性均取得了最大的資訊增益，可以隨機選擇其中之一作為劃分屬性（不防選擇“根蒂”）。因此可得：


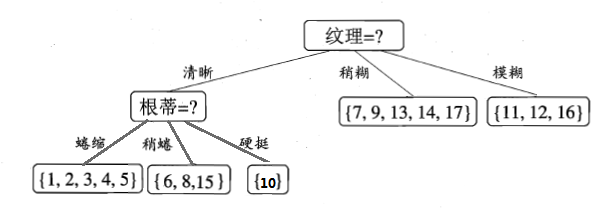
第三步,繼續對上圖中的每個分支結點遞迴的進行劃分，以上圖中的結點{“根蒂=蜷縮”}為例，設該結點的樣本集為，共5個樣本，但這5個樣本的class label均為“好瓜”，因此當前結點包含的樣本全部屬於同一類別無需劃分，將當前結點標記為C類（在這個例子中為“好瓜”）葉節點，遞迴返回。因此上圖變為：

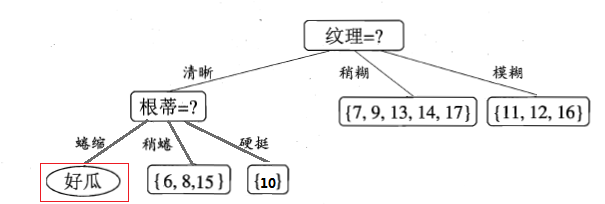
第四步，接下來對上圖中結點{“根蒂=稍蜷”}進行劃分，該點的樣本集為，共有三個樣本。可用特徵集為{色澤，敲聲，臍部，觸感}，同樣可以基於計算出各個特徵的資訊增益，計算過程如下（寫的比較詳細，方便大家弄懂）：

（注：該圖片版權所有，轉載或使用請註明作者（天澤28）和出處）
不妨選擇“色澤”屬性作為劃分屬性，則可得到：

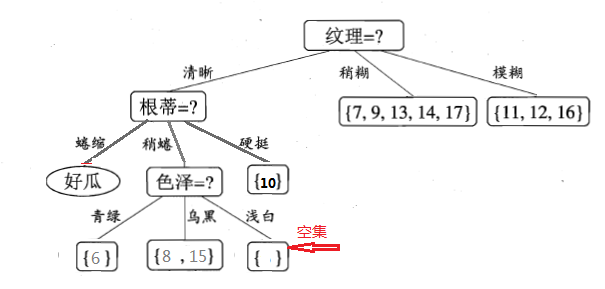
繼續遞迴的進行，看“色澤=青綠”這個節點，只包含一個樣本，無需再劃分了，直接把當前結點標記為葉節點，類別為當前樣本的類別，即好瓜。遞迴返回。然後對遞迴的對“色澤=烏黑”這個節點進行劃分，就不再累述了。說下“色澤=淺白”這個節點，等到遞迴的深度處理完“色澤=烏黑”分支後，返回來處理“色澤=淺白”這個節點，因為當前結點包含的樣本集為空集，不能劃分，對應的處理措施為：將其設定為葉節點，類別為設定為其父節點（根蒂=稍蜷）所含樣本最多的類別，“根蒂=稍蜷”包含{6,8,15}三個樣本，6,8為正樣本，15為負樣本，因此“色澤=淺白”結點的類別為正（好瓜）。最終，得到的決策樹如下圖所示：

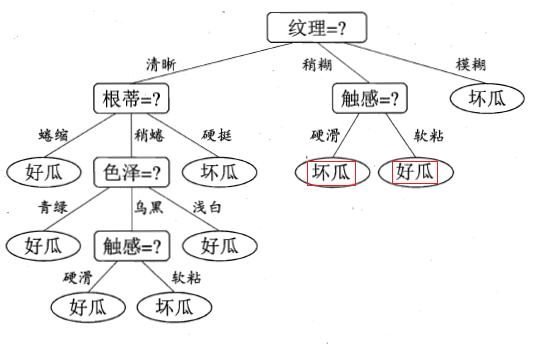
注：上圖紅色框起來的部分，是西瓜書印刷錯誤，上圖已改正。周老師在他的勘誤網站也有說明，詳見勘誤網站

說了這麼多，下面就來看看用決策樹演算法跑出來的效果，本人主要用weka的ID3演算法（使用的資訊增益），以供大家參看，後面還會放出自己實現的版本，後面再說。（之所以不要sklearn庫裡的決策樹，是因為sklearn庫裡的決策樹提供的是使用Gini指數優化後的CART，並不提供ID3和C4.5演算法）。
由於新版本weka裡已經不再提供ID3演算法了，只能下載另外的安裝包，把下載方法也貼出來吧，開啟weka的Tools->package manager在裡面找到包simpleEducationalLearningSchemes安裝即可。安裝好後就可以把西瓜資料集2.0來測試了，不過要想在weka中構建模型，還要先把.txt格式轉換為.arff格式，轉換的程式碼以及轉換好的資料集，詳見github。另外simpleEducationalLearningSchemes提供的ID3並不像J48那樣支援視覺化，因此參考連結基於以前weka老版本寫的視覺化，但該程式碼在新版本中無法使用，我修改了下整合到ID3上了，現在可以支援視覺化了，測試西瓜資料集，生成的視覺化樹如下，具體程式碼也放到了github上，有興趣的可以看看。




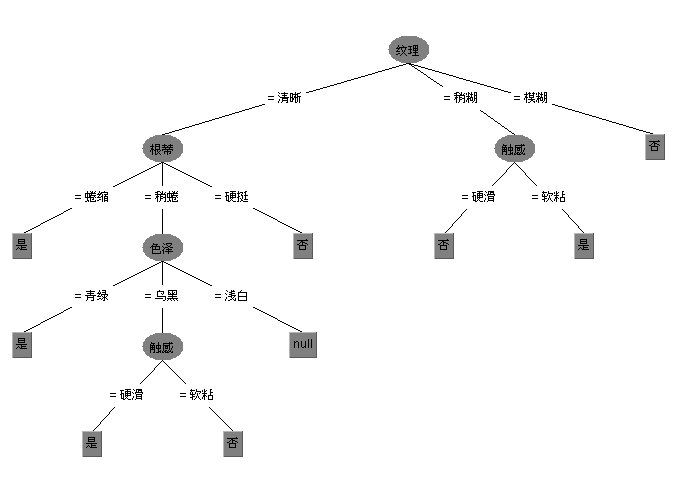
但資訊增益有個缺點（前面也說了）就是對可取數值多的屬性有偏好，舉個例子講，還是考慮西瓜資料集，如果我們把“編號”這一列當做屬性也考慮在內，那麼可以計算出它的資訊增益為0.998，遠遠大於其他的候選屬性，因為“編號”有17個可取的數值，產生17個分支，每個分支結點僅包含一個樣本，顯然這些分支結點的純度最大。但是，這樣的決策樹不具有任何泛化能力。還是拿西瓜資料集2.0來測試下，如果考慮編號這一屬性，看看ID3演算法會生成一顆什麼樣的決策樹：

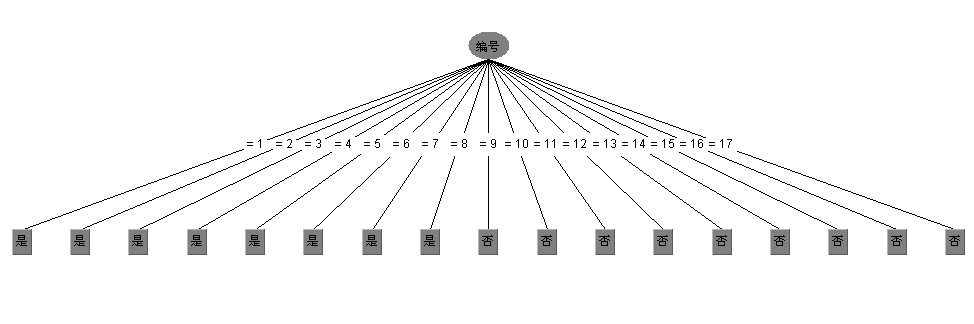
顯然是生成了一顆含有17個結點的樹，這棵樹沒有任何的泛化能力，這也是ID3演算法的一個缺點。另外補充一下ID3演算法的詳細情況：
  • Class for constructing anunpruned decision tree based on the ID3 algorithm. 
  • Can only deal with nominal attributes. No missing values allowed. 
  • Empty leaves may result in unclassified instances. For more information see: R. Quinlan (1986). Induction of decision trees. Machine Learning. 1(1):81-106.
由於ID3演算法的缺點，Quinlan後來又提出了對ID3演算法的改進C4.5演算法（在weka中為J48），C4.5使用了資訊增益率來構造決策樹，此外C4.5為了避免過擬合，還提供了剪枝的功能。C4.5還能夠處理連續值與缺失值。剪枝與連續值和缺失值的處理在下一篇部落格中再介紹。先來看看資訊增益率：
  • 資訊增益率
資訊增益比的定義為：

其中：

IV(a)成為屬性a的“固有值”，屬性a的可能取值數目越多（即V越大），則IV(a)的值通常會越大。例如還是對西瓜資料集，IV(觸感）=0.874(v=2)，IV(色澤)=1.580（V=3），IV（編號）=4.088（V=17）。但增益率也可能產生一個問題就是，對可取數值數目較少的屬性有所偏好。因此，C4.5演算法並不是直接選擇使用增益率最大的候選劃分屬性，而是使用了一個啟發式演算法：先從候選劃分屬性中找出資訊增益高於平均水平的屬性，再從中選擇資訊增益率最高的。來看看C4.5在西瓜資料集上構造的決策樹：

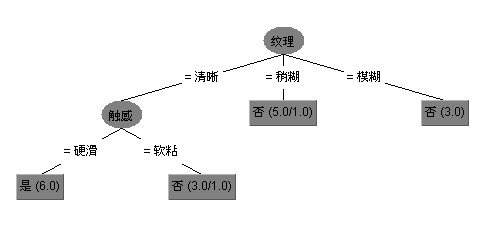
來看下混淆矩陣（Confusion Matrix）


有兩個樣本被誤分類了。
另外還可以用基尼指數來構造決策樹，像CART就是用基尼指數來劃分屬性的，來看下基尼指數：
  • 基尼指數
        基尼指數（Gini index）也可以用於選擇劃分特徵，像CART（classification and regression tree）決策樹（分類和迴歸都可以用）就是使用基尼指數來選擇劃分特徵。基尼值可表示為：

Gini(D)反應了從資料集D中隨機抽取兩個樣本，其類別標記不一致的概率，因此，Gini(D)越小，則資料集D的純度越高。則屬性a的基尼指數定義為：

所以在候選屬性集合中國，選擇那個使得劃分後基尼指數最小的屬性作為最優劃分屬性。
下面是用python的scikit-learn庫中提供的CART在西瓜資料集上的測試效果：
17個樣本全部拿來當做訓練集：


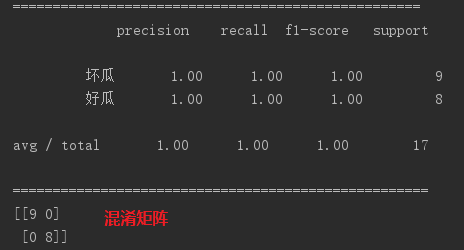
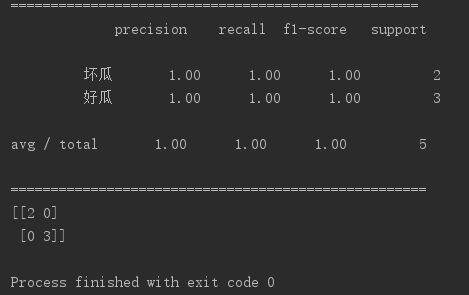
拿出25%的樣本當做測試集：

相關文章