微信小遊戲之跳一跳-電腦自動跳躍

應用環境

• android手機，需要啟用開發者模式。
• 電腦端的程式碼採用matlab編寫。
• 手機端和電腦端使用usb資料線連線。
• 電腦端通過adb命令向手機傳送相應的命令。
• 蘋果手機不支援（越獄的話也許可以，不過需要找到相應的adb
  adb
  命令）

本人手機為中興BA910，螢幕解析度1280∗720

，螢幕尺寸為5.1英寸，其他解析度以及尺寸的手機需要修改相應的程式碼引數以進行適配。

完整的程式碼我放在了github上了，github地址：
https://github.com/lpstudy/jump-wechat-game

請注意：
上述的程式碼是我一個下午加上晚上前2個小時所寫，包括想法，設計，程式碼除錯，以及遊戲測試，因此我基本上是以C

的語法在寫matlab，程式碼實在是醜陋不堪，自己由於科研方面的壓力也沒有精力去完善它，甚至於優化它。真的請見諒，我只想記錄一下自己當時的想法，也希望能夠給其他想做這個的一點哪怕小小的幫助，我就很滿足了。

遊戲的效果（跑了幾十分鐘，得了4096分，程式依然在執行，不得已手動掛掉它）：

背景介紹

大約幾天以前，聽說微信更新了版本，小程式中增加了一個小遊戲叫“跳一跳”，於是乎，我也更新了一個，開啟玩了玩，一直都是100

分左右，那叫個難受。

遊戲介面大概是這個樣子的：

遊戲規則

遊戲的過程就是通過按住螢幕，使得立著的那個小人距離向目標塊上跳躍，如果跳不到目標方塊上，那麼遊戲就失敗了，分數是根據小人跳躍的塊數逐步累加的。遊戲者按住螢幕的時間越長，小人跳躍的越遠，我們在遊戲中要根據小人距離目標塊的距離，來控制按住螢幕的時間，以儘可能的跳躍到目標塊的中心，這樣不僅有額外的加分，還因為有些目標塊很小，不在中心的話，很容易掉下來。
我當時想著操作那麼簡單，是不是可能能夠藉助電腦幫我弄呢？

我的一些思路

連線手機

adb命令

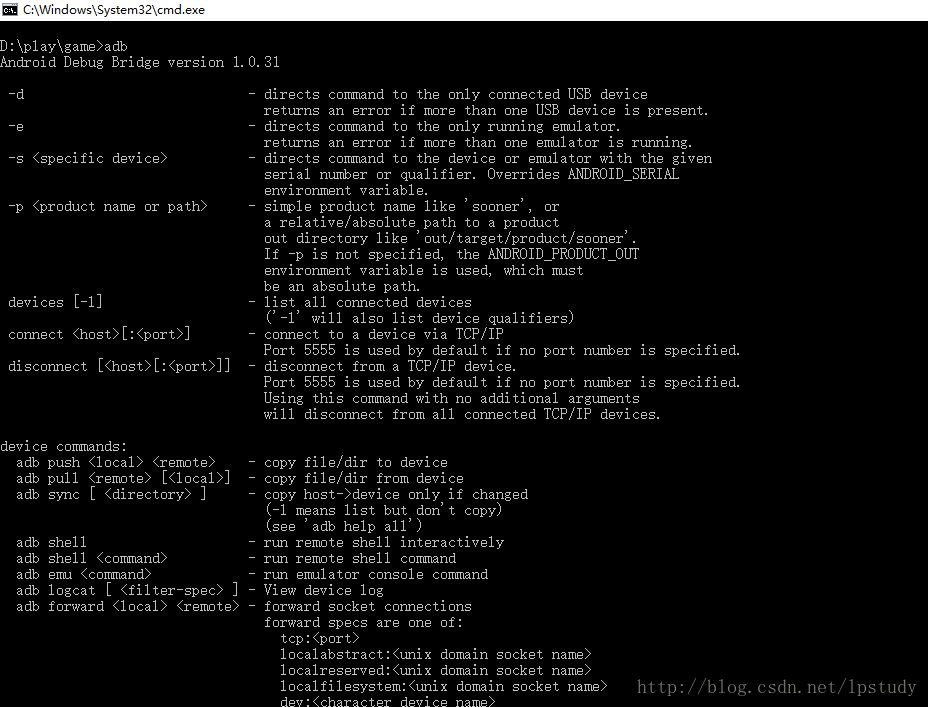
既然要用電腦去分析，那麼首先需要能夠通過電腦給手機傳送按壓螢幕的指令，我原來簡單玩過android，因此知道有個adb的東東，可以連線到手機端的shell，進行各種各樣的操作。我於是下載了adb，並把它加入到windows 系統的環境變數裡面，這樣就可以通過命令列使用adb命令了。

adb命令的一個幫助介面：

檢視手機裝置是否連線

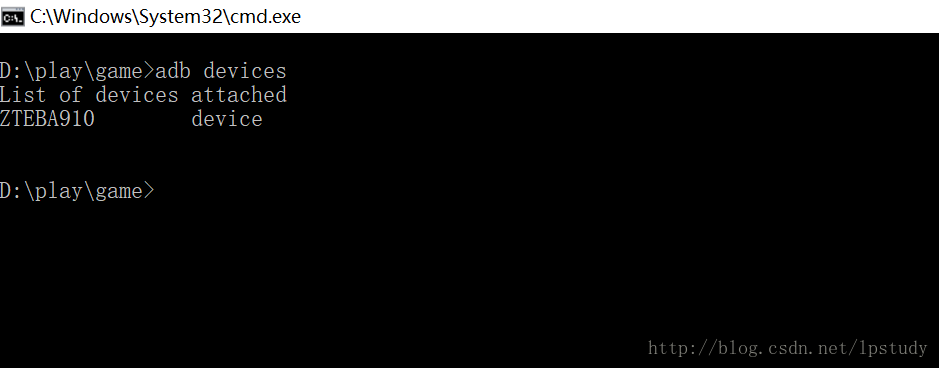
當adb命令可以正常使用後，還需要將手機通過usb資料線與電腦連線起來，手機端需要啟用開發者模式，開啟usb除錯選項，電腦端需要安裝手機的驅動程式（我一般都是直接安裝一個手機管家之類的電腦端軟體，只要它能夠識別手機，那麼驅動程式可認為已經安裝OK了），這個時候使用以下命令，檢視裝置：
adb devices
如果你的手機正常連線手機，那麼會看到有一行裝置，如圖

與遊戲相關的adb指令

經過搜尋之後，發現下面的兩個關鍵命令

• 擷取螢幕
  adb shell screencap -p /sdcard/screen.png
  上述命令擷取螢幕並儲存到sdcard中，可以使用
  adb pull /sdcard/screen.png來將圖片下載到電腦中

• 觸控螢幕命令
  adb shell input swipe 100 500 100 500 ms
  其中的ms表示觸控螢幕的毫秒數，這個在判斷好距離之後，得到相應的ms數，就可以向手機傳送觸控螢幕命令。

程式思路框架

擷取手機螢幕

利用上述的adb命令將手機螢幕的圖片擷取下來，這樣就可以放在電腦上分析一下當前圖片，為了方便，我寫了一個bat指令碼來對手機進行截圖，並將圖片下載到電腦端。

@echo off
:: capture screen
adb shell screencap -p /sdcard/%1
adb pull /sdcard/%1

將上述程式碼命名為capture.bat，然後就可以在cmd命令下執行它了，如下圖：

圖中的命令表示將手機端的螢幕圖片下載到電腦端，並儲存為1.png。

處理圖片

當拿到遊戲螢幕後，我的目標分為兩個步驟，（1）是計算出小人距離目標方塊的距離，即dis；（2）根據距離dis來計算出要觸控的毫秒數。

由於步驟1和2是整個工作的核心內容，因此單列2個大節分別講述。

執行觸控命令

根據前面步驟計算出的毫秒數，假定為666ms，然後執行觸屏命令：
adb shell input swipe 100 500 100 500 666
這樣手機端就像手按壓螢幕一樣，小人開始發起跳躍。

%向手機傳送觸控螢幕指定時間y的命令，並停頓1s
command = ['adb shell input swipe 100 500 100 500', ' ', num2str(round(y))];
fprintf('%s\n', command);
system(command);
pause(1)

圖片分析核心步驟

計算出小人距離目標方塊的距離

為了計算出小人距離目標方塊的距離，需要兩個要素，一個是小人的位置source，一個是目標方塊的位置target。在知道兩個要素的座標之後，可以直接使用兩個點的距離公式代入計算(target-source)^2。

圖片預處理之邊緣檢測-圖片二值化

螢幕擷取的圖片是RGB的，不僅計算量很大，還複雜，因此首先將其灰度化，然後尋找其邊緣，這樣不僅尋找目標簡單，而且整個圖片都可以轉換為一個二值圖片。

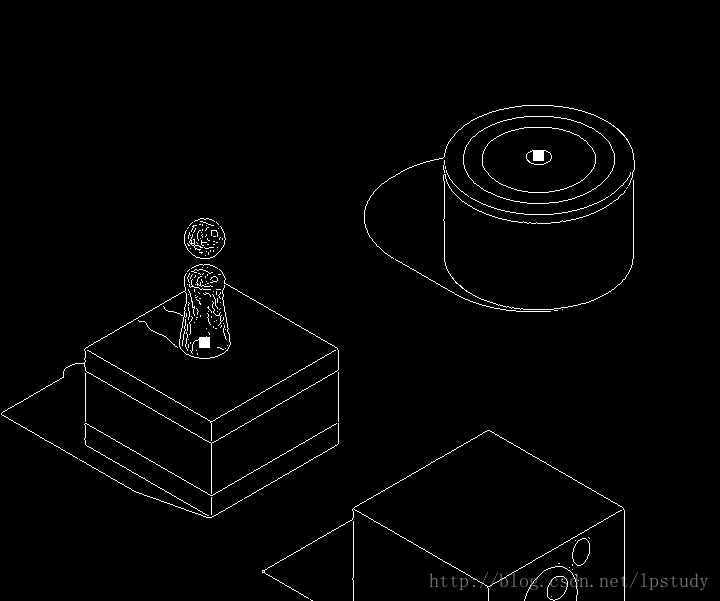
下圖是原始圖片和邊緣化之後的對比圖：

可以看出這個出來的邊緣還是非常清晰的，為了分析的方便，我將此圖的上面的分數部分和下面的一段切掉，如下圖所示：

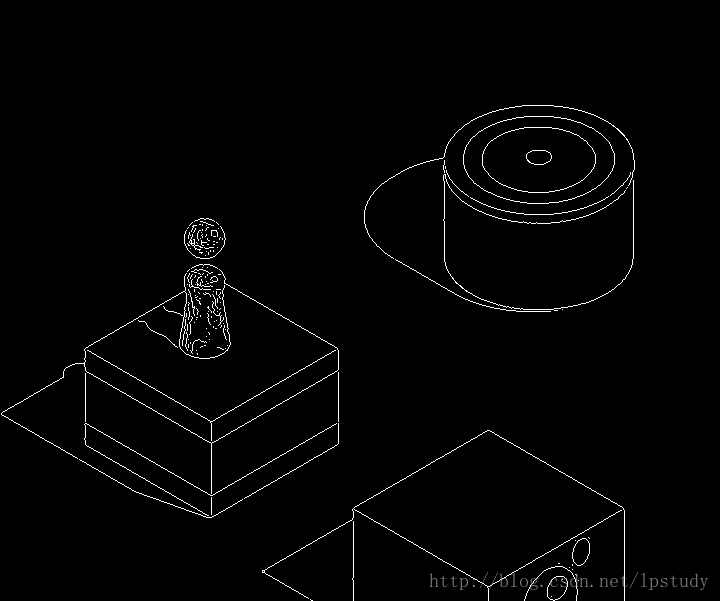
這樣看起來是不是很清楚了，有小人，有目標方塊，你肯定想問我，別說了，程式碼拿回來（其實我想說，程式碼我是從網上隨便找的一份，簡單修改了一下，已經不知道它的出處了）

filename = 'ori_2.png';
ori=imread(filename);
ori = specialcase(ori);
ori=rgb2gray(ori);
%轉化成灰度圖 
ori=im2double(ori);
%函式im2double 
%使用垂直Sobcl箅子．自動選擇閾值 
[VSFAT Threshold]=edge(ori, 'sobel','vertical');
%邊緣探測 
f=edge(ori,'sobel',Threshold/6);
f = f(400:1000, :);
imwrite(f, strcat('result\edge_cut', filename)) 

上述的程式碼自動選擇閾值Threshold，用來分辨邊緣，但是我實踐下來感覺解析度還不夠，因此我隨便寫了一個Threshold/6作為閾值，進行邊緣檢測，隨後使用400:1000進行切割圖片（這個值你可能需要改動，因為我的螢幕解析度是1280*720的，因此可以這樣寫死）。

上面的程式碼還呼叫了一個specialcase的函式，這主要是因為有兩種顏色的盒子與背景很相似，每次都不能正確找到邊緣。對於這兩個型別顏色的盒子，我直接暴力修改它的顏色，specialcase的程式碼如下：

function [f] = specialcase(f)
    [a,b,c] = size(f);
    for i = 1:a
        for j = 1:b
            if f(i,j, 1) == 255 && f(i,j,2) == 238 && f(i,j,3) == 97 || f(i,j, 1) == 186 && f(i,j,2) == 240 && f(i,j,3) == 68
                f(i,j,1) = 100;
                f(i,j,2) = 149;
                f(i,j,3) = 105;
            end
        end
    end
end

小人的位置

經過上述預處理之後的圖片，就是二值圖片了。小人就是一個輪廓而已。為了尋找它在圖片中的位置，我採用了模式匹配的思想，首先挖出幾個小人圖片作為模板，然後利用圖片滑動思想，將小人圖片在大圖片中滑動，逐個對比小人圖片與大圖片相應的方框，檢視其相似度，如果相似的話，那麼就找到了大圖片中的小人了。

小人模板圖片：

大圖的其中幾個框：

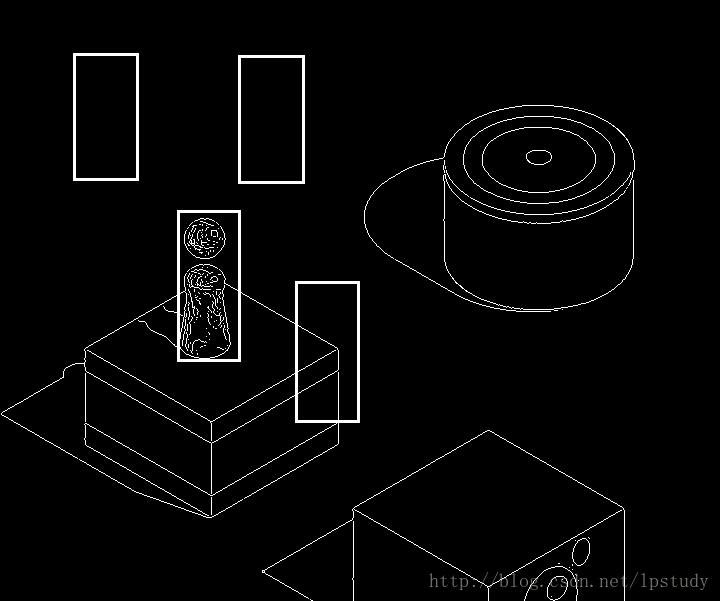
事實上每個框的size都和小人是完全相同的（我是手畫的，可能看起來不完全一樣），小人圖片如上圖所示，在上圖中逐個畫素滑動。滑動到一個方框後就比較小人和方框的相似度。

假定小人圖片為p

，大圖中的一個框為s，p中黑色點的個數為total，且黑色點對應的索引位置為index，s(index)為白色的點個數為cur，那麼相似度ratio記為cur/total，也就是說以匹配小人黑色點的比率作為度量。大圖中的某一個小框對應index位置的白色點與小人中黑色點匹配的越多，則越相似。我簡單實驗了一下，使用了0.5作為閾值，即ratio>0.5表明此小框就是小人。

有可能一個小人模板在整個圖片中都找不到ratio>0.5

的方框，因此我切割出了4的不同的小人作為模板。

 %使用多個模板進行匹配，直到有一個匹配成功
    res_i = 0;
    res_j = 0;
    finish = 0;
    for sample = 1:4
        if finish == 1
            break 
        end
        %template person
        t = imread(['samples\persons\', num2str(sample), '.bmp']);
        [a, b] = find( t == 0); %find the edge
        t = t(min(a):max(a), min(b):max(b));
        [m,n] = size(t);
        [row, col] = find(t==0);

        for i = 100:M-m
            if finish == 1
                break 
            end
            for j = 1:N-n
                if finish == 1
                    break 
                end
                total = length(row);
                cur = 0;
                for k = 1:total
                    if f(i+row(k), j+col(k)) == 1
                        cur = cur + 1;
                    end
                end
                ratio = cur * 1.0/total;
                if(ratio > 0.5)
                    fprintf('ratio=%.2f, i=%d, j=%d, filename=%s', cur * 1.0 / total, i, j, filename)
                    res_i = i;
                    res_j = j;
                    finish = 1;
                end
            end
        end
    end

    if finish == 0
    i = randi(3000000);
        fprintf('I can not find the little person, please refer the hardpics directory to check %d.png\n', i)
        figure(3), imshow(f), title('f.png')
        imwrite(f, strcat('hardpics\', filename));
        return
    end

程式碼中使用了多個模板，與大圖中逐個進行框，計算出cur

和total，如果ratio>0.5，程式就停下來，finish=1，這個時候我們得到小人的左上角的位置為res_i,res_j。如果找不到小人，程式會直接退出，並儲存圖片到指定位置，以便於二次檢查（跑了很多個小時，從沒有碰到過找不到小人的情況）。

計算目標方塊的位置

我們知道小人是向左上或者右上跳躍的，也就是說，肯定是向上跳躍的，因此，從上向下逐行掃描找到大圖中第一個白色的點，那就是目標方塊的上邊角，然後將其向下平移幾十個畫素，就基本到達它的中心位置了。

它的原始大圖如下圖所示：

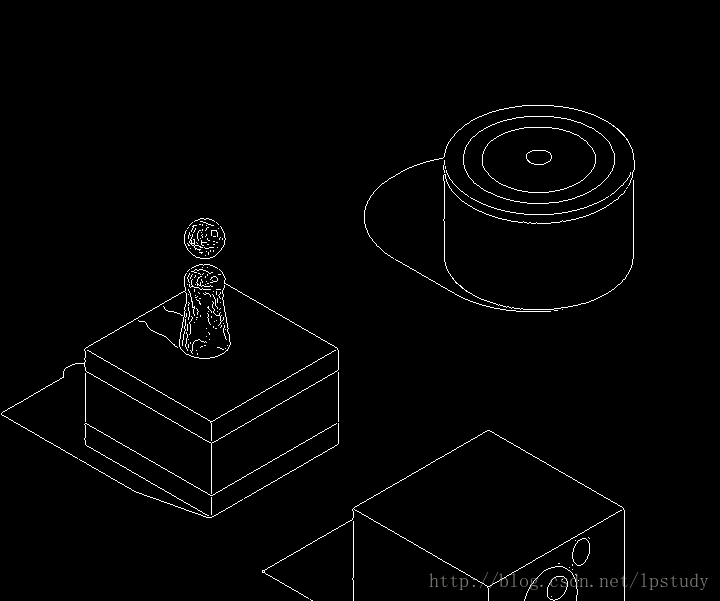
基於以上思路，先尋找它的上邊角。我們知道小人的頭有點高，有可能它的頭有可能超過目標方塊的上邊角，因此先把小人扣出去。

%remove the little person, in case it made some mistakes
remove_f = f;
remove_f(res_i:res_i+m, res_j:res_j+n) = 0;

在扣除小人後，我們得到remove_f如下圖所示：

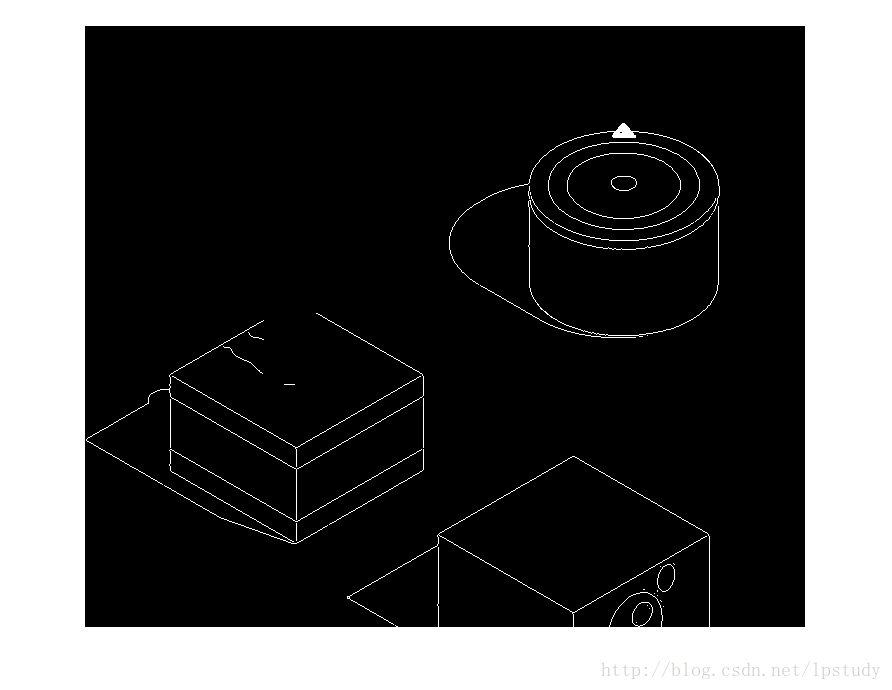
然後計算它的目標方塊的上邊角，就是上圖中圓柱體最上邊的那個點（我用白色的三角形進行了標記）。

% get top i and top j
[x, y] = find(remove_f == 1);
top_i = min(x); 
top_j = round(mean(find(remove_f(top_i, :) == 1)));

隨後，需要判定上圖中的白色三角形需要向下平移多少個畫素才到達目標方塊的中心點。我首先設定了兩個閾值18

和50，也就是說通過程式跑的計算出的平移量必須在18和50之間。程式從白色三角形，向下逐行掃描為白色（即1）的點的位置。對於每一行，用最右邊的白色點的位置減去最左邊白色點的位置，得到寬度width。從圖片可以看出，最上方的時候width很小，然後隨著向下掃描，width逐漸增加，隨後width穩定一個值不變，隨後又會變小。我們找到width穩定的那個中間點，作為它向下平移的距離，記作center。

舉例：假定我們找到的width

從上到下按照順序依次為1,3,6,10,13,14,15,22,25,25,25,25,25,22,18這樣的序列，那麼我們知道25就是它穩定的值。由於有5個25，我們選用中間的25所在的位置作為center值，這個數列中間的25是第11個數，因此center=11，也就是說上圖中的白色點需要向下平移11個畫素。

%from top_i to down, it is x axis. 
wids = zeros(1,top_i+200);
center = -1;
for i = top_i : top_i + 200
    index = find(remove_f(i,:) == 1);
    width = max(index)-min(index);
    if isempty(width)
        width = wids(i-1);
    end
    wids(i) = width;
    if i-top_i > 0 && width < wids(i-1)
        last = i-1;
        start = 0;
        for j = i-1:-1:top_i
            if not(wids(j) == wids(i-1))
                start = j+1;
                break
            end
        end
        if last-start>8
            last = start + 4;
        end
        center = round((start+last)/2)-top_i;
        break;
    end
end

if center < 18
    center = 18;
end
if center > 50
    center = 50;
end

計算小人的中心點：
小人的中心點可以根據小人左上角的位置res_i,res_j

進行平移，我們認為它的腳下正中間是小人的中心點，m為小人的高度，n為小人的寬度，減去15是向上平移15個畫素作為中心。

source_i = res_i + m - 15;
source_j = res_j+round(n/2); %腳跟距離腳的中心，需要向上提15個畫素

計算目標方塊的中心點：
目標方塊的中心點，列已經確定了，只需要行向下平移center

個畫素即可。

%calculate distance
target_i = top_i + center;
target_j = top_j; %最上方的那個點，向下平移50個畫素，認為是center。

如下圖所示：

然後根據source

和target計算小人和目標方塊的距離，即

%計算距離
dis = sqrt( (target_i-source_i)^2 + (target_j-source_j)^2 ) ;
fprintf(' dis = %.2f\n', dis)

根據距離dis來計算出要觸控的毫秒數

我們需要制定一個字典，來根據距離dis

得到相應的毫秒數ms。 我才用的是比較原始的方式，手機端啟動遊戲，然後電腦端執行上述的程式碼，得到dis，然後估計一個時間，例如500ms，通過adb給手機傳送觸控螢幕500ms的指令。 如果小人能夠正確落到標記的目標方塊點，就記錄這個(dis,ms)到字典dict中，慢慢的，我可以收集10幾個點。

有了這些點，我畫了一個點圖，感覺像是線性的，因此就簡單使用了matlab中自帶的一元線性擬合的程式碼，擬合的一條直線（猜測是最小二乘法）。這樣，隨後給出任意的dis

，都可以根據直線方程得到相應的ms。

線性擬合的程式碼如下：

%根據距離，以及擬合的直線，得到相應的毫秒數 y
dict = [
    [163,350], [197.04, 420], [207, 430], [270, 550], [287, 570], [310, 640], [321, 670], [348.63, 730], [367.27, 769],[374, 780],[393.61, 800], [409.93, 841] 
];

x = dict(1:2:end);
y = dict(2:2:end);

p = polyfit(x,y,1);
y1=polyval(p,x);  %計算出擬合的y值
%figure(3),plot(x,y,'k*',x,y1,'r-');  %畫出資料對比圖，黑點是原始資料，紅線是擬合曲線
y = polyval(p, dis);

本人lpstudy，轉載請註明出處，謝謝。