EM演算法學習筆記

garfielder007發表於2016-05-08

宣告：

1）該博文是多位博主以及書籍作者所無私奉獻的論文資料整理的。具體引用的資料請看參考文獻。具體的版本宣告也參考原文獻

2）本文僅供學術交流，非商用。所以每一部分具體的參考資料並沒有詳細對應，更有些部分本來就是直接從其他部落格複製過來的。如果某部分不小心侵犯了大家的利益，還望海涵，並聯系老衲刪除或修改，直到相關人士滿意為止。

3）本人才疏學淺，整理總結的時候難免出錯，還望各位前輩不吝指正，謝謝。

4）閱讀本文需要機器學習、概率統計演算法等等基礎。

5）本人手上有word版的和pdf版的，有必要的話可以上傳到csdn供各位下載

一．EM演算法解決的問題

要了解EM演算法，就先了解這個演算法是幹啥的，十大演算法之一頭銜怎麼來的。當然這個頭銜是專家們投票得來，只是這個投票跟現在的選秀節目投票不一樣，EM是憑藉硬實力勝出的，有鐵桿粉絲稱之為“神的演算法”。

EM演算法之前，先要了解極大似然估計方法，這個在轉發的博文《從最大似然到EM演算法淺解》裡面有講解了。

極大似然估計能解決很大一部分的引數估計問題了，類似邏輯迴歸，RBM等等，都看到了它的影子，確實及其常用。

然而極大似然估計也是有極限的，起碼基本的要求是：樣本都是來自同一個分佈的，然後就幫忙估計這個分佈的引數（如高斯分佈，就估計均值和方差，這兩個量都是引數）。

當遇到下面的情況：樣本來自多個分佈的。簡單地說就是樣本的一部分來自分佈A，又有一部分來自分佈B，……，這樣就有多個分佈了（當然，資深的數學愛好者還會認為這麼說不對，他們認為應該是樣本里面的每一個個體都是一部分屬於分佈A，一部分屬於分佈B，……，也就是說樣本的每個個體都是按概率屬於多個分佈的）。然後還有一個制約就是：每個樣本都不知道來自哪個分佈的。

要估計這麼多個分佈的引數，極大似然估計就不行了，這一團糟的場面它處理不了。

EM演算法就是專門解決這種疑難雜症的，方法也快刀斬亂麻：直接每個個體胡亂指一個分佈，然後就分別去估計每個分佈的引數；估好後再根據情況把每個個體調節一下，該屬哪個分佈就分配到哪個去，然後再估計每個分佈的引數（江湖上也是這麼來的，一開始小弟們都隨便認個老大，結成各個幫派，然後幫派之間又選取新老大，選完後不爽的小弟就跳槽到他爽的老大那去；跳完後各個幫派又開始選老大，小弟又洗牌，最後穩定下來的，就成了江湖）。

為了方便描述，舉個例子，暫且認為江湖上只有兩個門派，高富帥派和矮窮醜派。有一天武林要舉行炫富大賽，兩大門派都派了4名高手去參加比賽。比賽過程不多說了，倒是這次比賽亮出來的財富亮瞎了某武林高手的狗眼，他很生氣，就派人抓了這8個人，當然為了比賽，這8位高手都穿得西裝革履的，外表看不出來哪個幫派的。這位高手很想知道哪些人是高富帥派的，哪些是矮窮醜派的，而且還想知道這兩派的實力，所以要知道這兩派的財富的均值和方差，還要知道兩派分別來了多少人。

這個時候，這位高手就只能用EM演算法了。

二．EM演算法數學描述

EM演算法分兩步，E步和M步，總的流程如下：

E步：對於每一個樣本，計算這個樣本屬於各個分佈的概率（指派每個樣本個體的歸屬，也就是求出來每個樣本屬於各個分佈的概率，從而確定 ${{\rm{q}}_i}\left( z \right)$ 這個分佈的概率密度函式，離散型的就是求到了概率）
${{\rm{q}}_i}\left( z \right): = p({\rm{z}}|{{\rm{x}}_i};{\theta ^{old}})$
M步：最大化似然Q函式，求得引數θ（這個θ包括了樣本所屬的每個分佈的裡面的所有引數，如100個高斯分佈，就求出了100個均值和100個方差），Q函式定義如下
${\rm{Q}}\left( {\rm{\theta }} \right) = \sum \limits_i \sum \limits_z {q_i}\left( z \right)ln\frac{{p({x_i},z|\theta )}}{{{q_i}\left( z \right)}}$
其中的 ${{\rm{q}}_i}\left( z \right)$ 表示樣本xi屬於各個分佈的概率密度函式，注意z這個東西，它可能有多種取值，也可能是個向量，甚至是連續的。是離散的情況的時候，只需要求每一種情況的概率，如果z^((i) )是連續值的時候， ${{\rm{q}}_i}\left( z \right)$ 要用概率密度函式或者概率函式表示， ${\theta ^t}$ 表示引數θ的上一輪的迭代值或者初始值。
總之在E步就需要得到每個樣本所屬的類別，這個類別指定可能只需要用一些簡單的量，那就把這個量求出來就可以了。E步求這個“所屬類別”的目的是為了寫出Q函式的形式來，而且這個形式不帶著隱變數，也就是z這個東西。這樣是為了保證能在求解問題的過程中不需要考慮隱變數，從而能想求解極大似然那樣，得到一個閉式解或者迭代的解法。
M步中的那個Q函式（名字千百種，這裡就叫這種吧），是每個樣本個體的對數似然函式 ${\rm{logp}}\left( {{x_i},z;{\rm{\theta }}} \right)$ 在條件概率分佈 ${q_i}\left( z \right)$ 下的期望（注意求期望其實是求積分），然後再對每個樣本的值都累加起來，得到了總的最大化的目標。

三．EM演算法數學基礎

來些數學上的描述，把符號交代一下吧。
問題可以描述成：給定觀測到的樣本集合x1,x2,x3…,xn，目標是找到每一個樣本個體隱含的類別z（注意z可能是由一個向量表示的），使得p(x,z)最大。
解法還是極大似然那一套，目標函式定義為
${\rm{l}}\left( {\rm{\theta }} \right) = \sum \limits_{i = 1}^n lnp\left( {{x_i};\theta } \right) = \sum \limits_{i = 1}^n ln \sum \limits_z p\left( {x,z;\theta } \right)$
要求的引數原來是θ，但是無端端多了個z，就不好辦了，閉式的迭代式都搞不出來了。
搞不出來也得想辦法搞，觀察樣本個體xi的對數似然，再看聯合概率，先不管引數θ，用貝葉斯定理展開

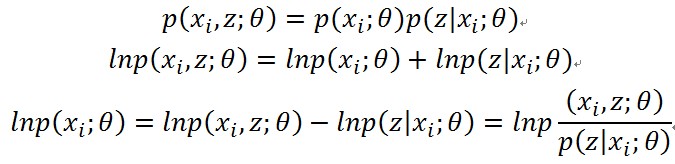
取樣本xi對隱變數z的分佈（也就是樣本xi屬於各個類別的概率）的總和，得到下面的全概率
$\sum \limits_z {q_i}\left( z \right) = 1$
把上面的東西加上來

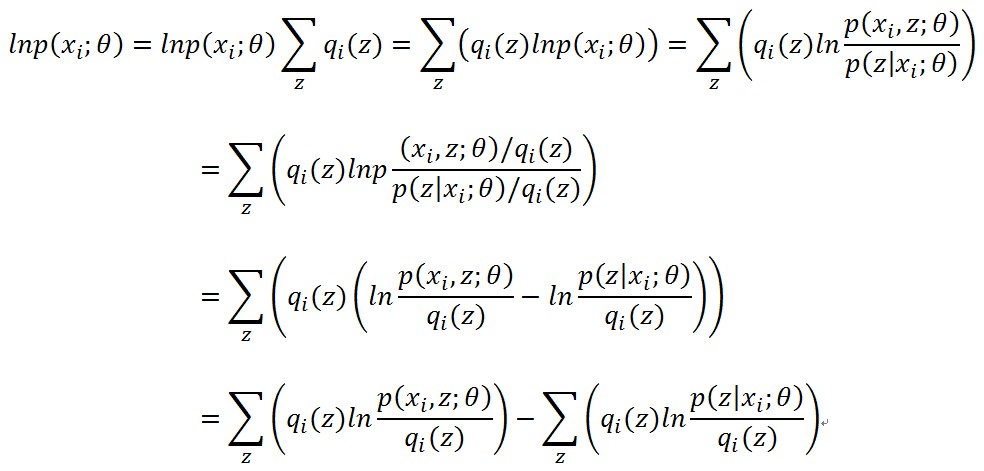
這裡可以看到，每個樣本的對數似然函式都分成了兩部分，分開討論吧，令

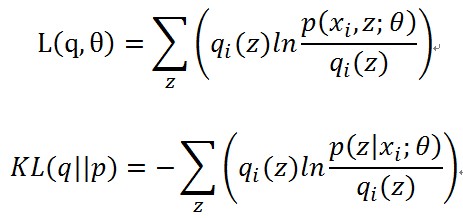
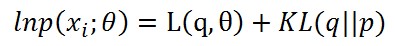（1）
那麼可以用下面的示意圖來表達對數似然函式值的分解

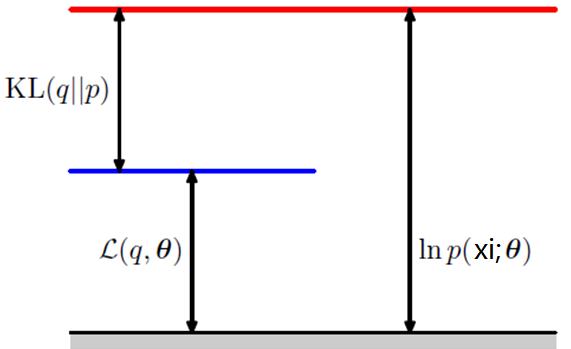
每個樣本個體都可以這樣劃分的，所以對數似然函式變成了下面的樣子

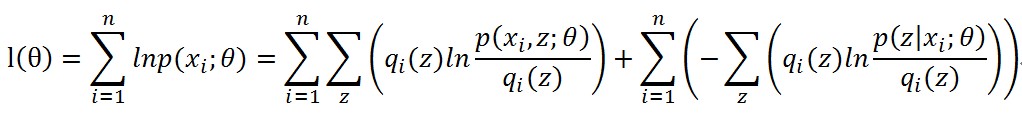
前半部分就是Q函式，後半部分就是每個樣本p分佈和q分佈的KL距離。
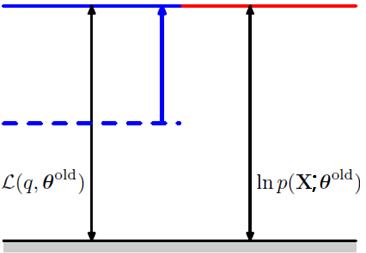
再看看E步做的事情， ${{\rm{q}}_i}\left( {\rm{z}} \right): = p(Z|{{\rm{x}}_i};{\theta ^{old}})$ ，這樣的結果令每個樣本的q和p分佈相同了，那麼就會出現KL(q||p)的值為0，這是KL距離的定義，但是由於等式（1）的存在，所以總的lnp(x_i;θ)值是不變的，那麼就是L(q,θ)的值提高了，這就保證了 $lnp\left( {{x_i};\theta } \right)$ 的累加和的下界被提高了，也就是對數似然函式的下界提高了。就像下面的圖表示的一樣。

再來看看M步做的事情，求Q函式的最大化，獲取了新的θ值θ^new。這樣導致的結果就是Q函式的值提升了，而且p和q分佈又不一致了，KL距離再度變大了，從而整體的對數似然函式的值也提升了。就像下面的圖表示的一樣。

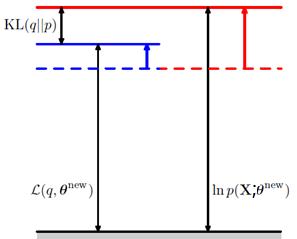
這樣兩步不斷地做，對數似然函式就不斷地被提升，直到逐漸收斂到一個對數似然函式序列的穩定點。如下面的示意圖。

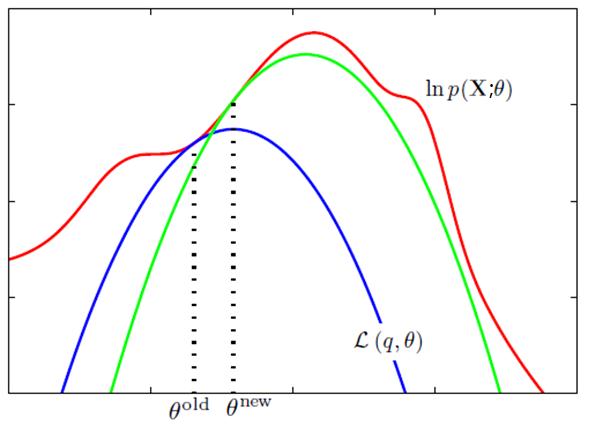
當然不能保證收斂到極大值點。初值選取對這個也有影響的，這個就不多討論了。

四．EM演算法實際例子

現在開始看（一）的那個例子，假設這八個人的財富值分別是0.8,0.9,1.0,1.3,9.8,9.9,10.0,10.3。
一開始不知道怎麼搞，當然在之前就認為他們各自的財富屬於一個正態分佈的，就亂假設：
假設矮窮醜派是1類，高富帥派是2類，用k指定，
再假設矮窮醜派財富均值 ${{\rm{\mu }}_1} = 2.0$ ，標準差 ${\delta _1} = 0.4$ ，也就是 ${\theta _1} = \left( {{{\rm{\mu }}_1},{\delta _1}} \right) = \left( {2.0,0.4} \right)$ ；
再假設高富帥派財富均值 ${{\rm{\mu }}_2} = 8.0$ ，標準差 ${\delta _2} = 0.6$ ，也就是 ${\theta _2} = \left( {{{\rm{\mu }}_2},{\delta _2}} \right) = \left( {8.0,0.6} \right)$ ；
當然 ${\rm{\theta }} = \left( {{\theta _1},{\theta _2}} \right)$ ，需要的話可以把這個寫成一個矩陣，這裡就不糾結符號的寫法了
再假設矮窮醜派的人數比例是 ${{\rm{\alpha }}_1} = 0.4$ ，高富帥派的人數比例是 ${{\rm{\alpha }}_2} = 0.6$ 。
一、開始E步，計算每個樣本歸屬，首先計算每個樣本屬於每個類別的概率值，根據
$\emptyset \left( {{\rm{y|}}{\theta _k}} \right) = \frac{1}{{\sqrt {2\pi } {\delta _k}}}{e^{ - \frac{{{{\left( {y - {\mu _k}} \right)}^2}}}{{2\delta _k^2}}}}$
來計算，得到一個樣本歸屬的矩陣A
0.0167 0.0001
0.0342 0.0001
0.0659 0.0001
0.3229 0.0001
0.0001 0.1111
0.0001 0.0067
0.0001 0.0038
0.0001 0.0007
又因為 $p\left( {{x_i},k{\rm{|}}{\theta _k}} \right) = {{\rm{\alpha }}_k}\emptyset \left( {{x_i}{\rm{|}}{\theta _k}} \right)$ ，這裡要注意，這個聯合概率還是得好好理解的，不然就混了。根據公式 $\frac{{{{\rm{\alpha }}_k}\emptyset \left( {{x_i}{\rm{|}}{\theta _k}} \right)}}{{ \sum \nolimits_k {{\rm{\alpha }}_k}\emptyset \left( {{x_i}{\rm{|}}{\theta _k}} \right)}}$ 計算每個樣本屬於每個類的概率，再歸一化後得到如下矩陣B，這個就是指派矩陣了。第一行說明第一個樣本個體有0.9999的概率屬於矮窮醜派，只有0.0001的概率屬於高富帥派。
0.9999 0.0001
0.9999 0.0001
0.9999 0.0001
0.9999 0.0001
0.0009 0.9991
0.0147 0.9852
0.0256 0.9743
0.1250 0.8750

二、開始M步
最大化Q函式
${\rm{Q}}\left( {\rm{\theta }} \right) = \sum \limits_i \sum \limits_k {q_i}\left( k \right)ln\frac{{p({x_i},k|{\theta _k})}}{{{q_i}\left( k \right)}}$
其中i=1,2……8，k=1,2。
且 $\frac{{p({x_i},k|{\theta _k})}}{{{q_i}\left( k \right)}} = \frac{{\emptyset \left( {{x_i}{\rm{|}}{\theta _k}} \right){{\rm{\alpha }}_k}}}{{{q_i}\left( k \right)}}$
把上面的值代進去，然後解這個優化問題，得到引數。