LDA入門級學習筆記

宣告：

1）該博文是多位博主以及科學家所無私奉獻的論文資料整理的。具體引用的資料請看參考文獻。具體的版本宣告也參考原文獻

2）本文僅供學術交流，非商用。所以每一部分具體的參考資料並沒有詳細對應，更有些部分本來就是直接從其他部落格複製過來的。如果某部分不小心侵犯了大家的利益，還望海涵，並聯系老衲刪除或修改，直到相關人士滿意為止。

3）本人才疏學淺，整理總結的時候難免出錯，還望各位前輩不吝指正，謝謝。

4）閱讀本文需要機器學習、概率統計演算法等等基礎（如果沒有也沒關係了，沒有就看看） 。

5）此屬於第一版本，若有錯誤，還需繼續修正與增刪。還望大家多多指點。請直接回帖，本人來想辦法處理。

6）本人手上有word版的和pdf版的，有需要的話可以上傳到csdn供各位下載，也可以到深度學習群裡去下載，或者發郵件到老衲郵箱：beiliude@163.com。

一．問題描述

傳說搜狗公司請了個大牛，把這方面搞得風生水起。最近組內的LDA用得風風火火的，組內同事也是言必稱LDA。
不花點時間看看，都快跟人說不上話了。
當然，學習東西慢就只好從簡單的開始了，所以把簡單的基礎的東西在這裡講講，希望能把基本問題講清楚，高深的推導就跳過了。

1.1文字建模相關

統計文字建模的目的其實很簡單：就是估算一組引數，這組引數使得整個語料庫出現的概率最大。這是很簡單的極大似然的思想了，就是認為觀測到的樣本的概率是最大的。
建模的目標也是這樣，下面就用數學來表示吧。
一開始來說，先要注意假設了一些隱變數z，也就是topic。每個文件都符合一個topic的分佈，另外是每個topic裡面的詞也是符合一個分佈的，這個似然是以文件為單位的。極大似然式子全部寫出來是下面的樣子的

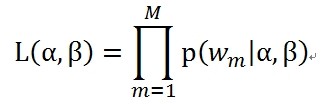
其中的M表示文件個數。其中的α，就是每個文件符合的那個topic分佈的引數，注意這個傢伙是一個向量，後面會再描述；其中的β，就是每個topic裡面的詞符合的那個分佈的引數，注意這個也是一個向量。
本來到這裡看起來挺簡單的，就是一個普通的極大似然估計，估計好引數α和β，就大功告成了。
如果是傳統的極大似然估計，好辦了，求個梯度，梯度為0的地方就是解了，這裡這個東西偏偏多了個隱變數，就是每個詞屬於哪個topic的？還有每個文件屬於哪個topic的？比如，每個文件的topic是怎麼分佈的（意思就是，每個文件是按概率屬於各個topic的，當然，各個topic的詞的分佈情況是不一樣的，比如有金融，電商兩種topic，文件有可能是0.3的概率屬於金融，0.7的概率屬於電商），還有文件裡面每個詞有來自哪種型別的詞的分佈的（意思就是，每個詞來自哪個topic的，每個topic裡面的詞分佈不一致的，如金融topic裡面“人民幣”這個詞的概率是0.7，“商品”這個詞的概率是0.3；電商topic裡面“人民幣”這個詞的概率是0.4，“商品”這個詞的概率是0.6）。
這個玩笑就開大了，直接求解就玩不動了，只好用其他演算法了。
候選的比較大眾的求解有隱變數的演算法有EM。
下面先把似然函式用全概率表示出來再做討論吧。
假設一個文件w_m的topic分佈（doc-topic分佈）已知，用向量θ_m表示（這個向量的每一項的和為1，總體可以表示一個概率分佈），每個詞來自哪個topic已知，用z_(m,n)表示，每個topic的詞分佈用矩陣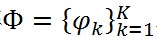中的一行（topic-word分佈）表示（這是一個K*V的矩陣，其中V表示語料庫中的詞的數量，第一行表示第一個topic裡面的詞分佈）。
在已知上面的這些條件的情況下，計算一個文件的整個聯合complete-data的聯合分佈（意思就是所以變數都已知的情況下）的式子如下
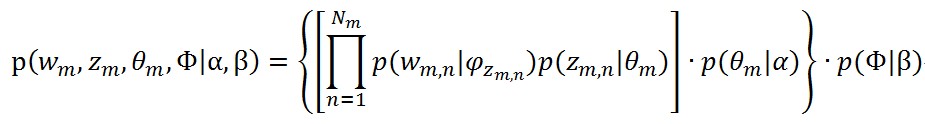    （3）
中括號裡面的是生成詞的過程，大括號裡面是生成文件的過程，最右邊的那個概率就是∅的後驗概率。注意z_m是一個向量，維度為Nm。
這麼一堆東西，還是很複雜的，中間有這麼多的奇怪的變數，計算起來的複雜讀可想而知了，為了跟似然函式聯絡起來，通過對θ_m（doc-topic分佈）和Φ（topic-word分佈）積分，以及對z_(m,n)求和，得到只有w_m的邊緣分佈

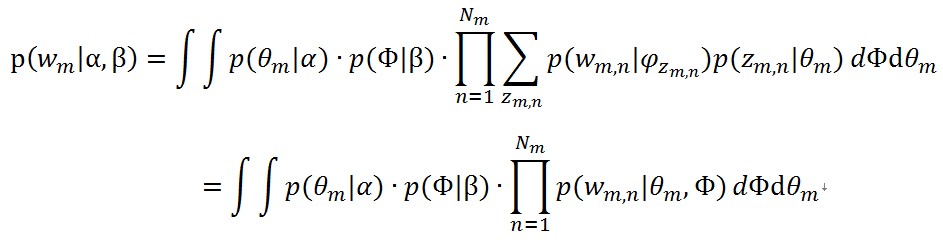
（4）
那個累加號被去掉的原因是：在引數θ_m和φ_(z_(m,n) )都已知的情況下，一個詞t被產生的概率是

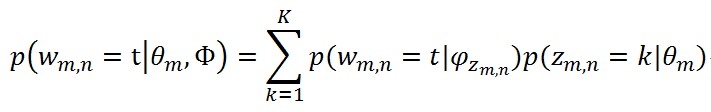
（5）
這下好了，每個文件的似然概率有了，可惜沒啥用，實際上這個邊緣分佈是求不出來的，因為z_(m,n)是隱藏變數，每個詞都跟θ_m和Φ都跟z_(m,n)有關，那個連乘又是非常難用積分得到的，這個就是耦合現象。要注意聯合分佈和邊緣分佈對z乘積與加和的區別。另外，有些文獻上是沒有Φ相關的項的，這個看起來各種費勁，以後想清楚後回來解釋。

1.1.1 概率公式相關討論

對於公式（3），要多討論點，這個是LDA模型的重要的東西，這裡說為啥公式是長這個樣子的。
先直接抄《LDA數學八卦》的例子，就是文件怎麼生成的，直接截圖如下

再不懂裝懂，搞個概率圖模型來看看。

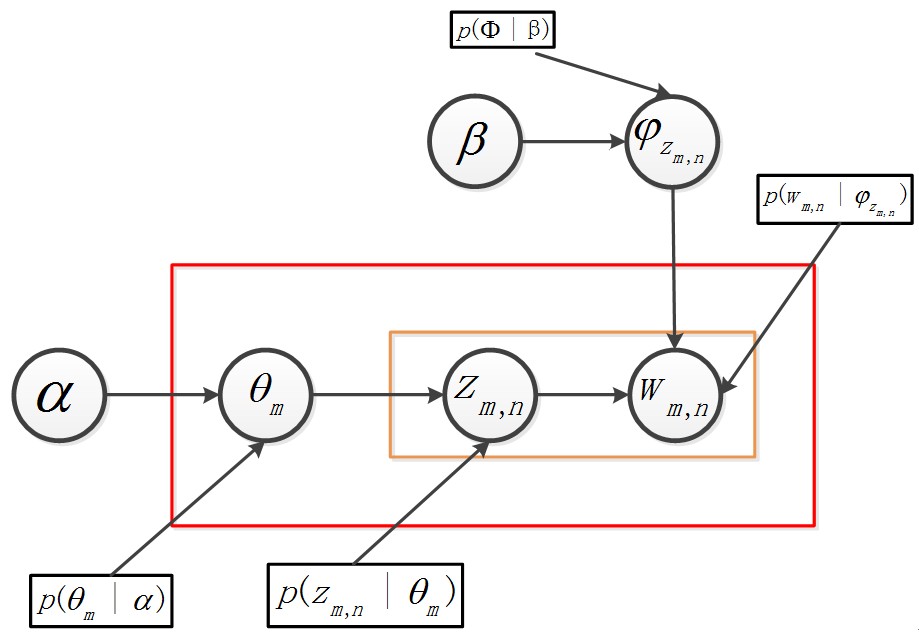
最上面的那個公式代表的就是步驟2——先弄K個topic-word骰子，為了符合貝葉斯學派的口味，這個K個骰子是有先驗分佈的，先驗分佈就是一個Dirichlet分佈，引數是β，具體在公式（3）中的表現為p(Φ|β)。
步驟3中，“抽取一個doc-topic骰子”，就是圖下面的那個第一個水平的箭頭，具體在公式（3）中表現為p(θ_m |α)。“投擲這個doc-topic骰子，得到一個topic編號z”這句話說的就是圖下方第二個水平的箭頭，具體在公式（3）中表現為p(z_(m,n) |θ_m)。步驟3中的第二步“選擇K個topic-word骰子中編號為z的那個，投擲這個骰子，得到一個詞”這句話說的是圖右上角那個垂直的箭頭，在公式（3）中具體表現為p(w_(m,n) |φ_(z_(m,n) ))。
就是這個過程，導致了公式（3）長成了現在這個樣子，夠複雜，而且夠棘手，直接去搞公式（4）來計算似然基本沒戲的。

1.1.2 似然函式求解

上面小節說過了，計算似然函式是沒戲的。
大眾候選演算法還有EM，其實也不能解這樣的問題，因為EM演算法依賴條件概率

其中的矩陣Θ，就是doc-topic分佈矩陣，是一個M*K的矩陣，只是這也是一個隱變數對應的引數，就是文件的topic的先驗分佈。
如果非要用EM演算法，這裡就需要利用另一個分佈去擬合這個條件概率，這個就是變分法。變分法的基本思想就是：因為條件概率不好求，但是聯合概率是已知的，就可以使用一種類似EM的方法，使用另外的一個概率函式去擬合要求的這個條件概率。具體資料以後再整理。
還好的是LDA沒有把引數α和β作為求解的最終目標，目標另有其人。
這個什麼極大似然，什麼語言模型是個幌子。就像word2vec裡面，其實目標是那些詞向量，也就是那些引數值。用LDA來解，就更離譜了，連引數α和β這兩個引數值都不是目標，而是那些隱變數對應的引數比較重要。
不管用什麼方法求解，這個LDA的目的是要做推理。
其實需要求的東西其實是下面的式子
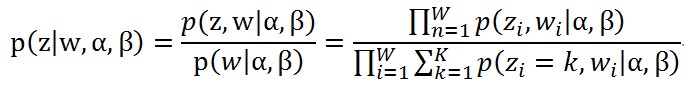       (6)
第一個等號後面的分母p(w_m│α,β)就是上面公式（4）的那個值，引數θ_m（doc-topic分佈）和Φ（topic-word分佈）不見了是因為這兩個量已經用觀察到的w_(m,n)和對應的z_(m,n)求積分得到了跟這兩個量無關的值，(論文上這個方法叫collapsed Gibbs Sampling，即通過求積分去掉一些未知變數，使Gibbs Sampling的式子更加簡單)，其實意思就是，引數θ_m和Φ已經使用MCMC的方法估算到了相應的值，估算的時候使用的樣本就是訓練樣本，這裡是一個奇怪的地方，有精力回來解釋得容易理解點。
就算是這樣，哪怕都搞走了這麼多引數，分母也不見得好求，一篇文章光求和的項就有K^(N_m )個。
到了這一步，其實大家應該明白了，為啥（6）要表示成那樣給大家看看，因為真的只是看看而已，還可以寫成其他表現形式，但都不重要了，最後都會給出一個結論的，這個分母沒法求，只好用其他辦法了。
公式（6）這個條件概率就是要擬合出來的分佈。當然，在擬合這個分佈過程中，產生了副產品——所有文件的在各個topic上的分佈。一旦α和β確定了，每個文件在各個topic上的分佈可以直接得到，這個副產品才是求解的目的。
現在問題明確了，貝葉斯推理需要公式（6）的分佈，擬合這個分佈中產生的副產品是LDA產出的結果，有這結果就能用來做推理。

二．問題求解

2.1 LDA模型求解目標

上面說清楚了，求解LDA就是擬合公式（6）的那個分佈，中間要把doc-topic分佈矩陣和topic-word分佈矩陣求出來。
論文總提到的方法是Gibbs Sample方法，下面就開始介紹。

2.1.1 LDA Gibbs Sample方法簡介

這裡介紹論文中的Gibbs Sample方法怎麼擬合的。
這個Gibbs Sample方法也不多介紹，因為具體沒弄得特別理解。只知道這個方法的具體步驟：假設觀測到的變數是x，隱變數是z（這兩個都是向量），通常需要整出來的都是條件概率p(z|x)，只是這個條件概率比較難求，只知道了聯合概率p(z,x)（必須知道），Gibbs Sample方法的處理方式就是構造下面的條件概率

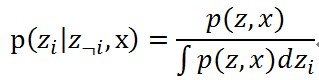
使用上面的條件抽取z的R個樣本z_r，r∈[1,R]，當樣本數量足夠多的時候，條件概率可以用下面的式子近似了

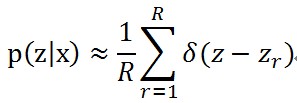
其中的δ函式形式是

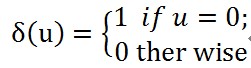
也就是，如果u是個0向量，就是1，否則是0.
解決的方案有了，還有個條件需要具備，就是聯合概率。

2.1.2求聯合概率

聯合概率表示如下

這個聯合分佈是公式（3）利用積分去掉了引數θ_m（doc-topic分佈）和Φ（topic-word分佈）得到的，可以看到右邊的式子，第一個概率跟α，第二個概率跟β無關。這樣這兩個概率就可以單獨處理了。
先看第一個分佈p(w|z,β)，如果給定了一組topic-word分佈Φ，這個概率可以從觀測到的詞中生成：

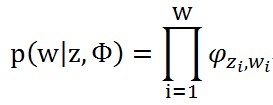
其中zi表示語料庫中的第i個詞的topic，wi表示語料庫中的第i個詞，W表示語料庫中的詞數。
意思是，語料庫中的W個詞是根據主題zi觀察到的獨立多項分佈(我們把每個詞看做獨立的多項分佈產生的結果，忽略順序因素，所以沒有多項分佈的係數)，就是一個多項式分佈。注意φ_(z_i,w_i )是矩陣Φ中的第zi行第i列的元素，順便提醒一下這個矩陣Φ其實就是LDA要學習的一個東西，是K*V的矩陣，K是topic數，V是詞彙數；另一個LDA要學習的東西就是矩陣Θ，也就是doc-topic分佈矩陣，是一個M*K的矩陣，矩陣的第一行表示第一個文件的topic分佈。
把這個概率拆分到矩陣Φ的每一行和每一列去，得到下面的式子

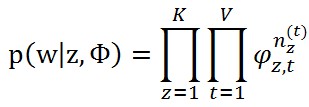
其中n_(z,t)表示詞t在topic z中出現的次數。
那麼要求的第一個分佈p(w|z,β)，就可以通過對Φ的積分來求得

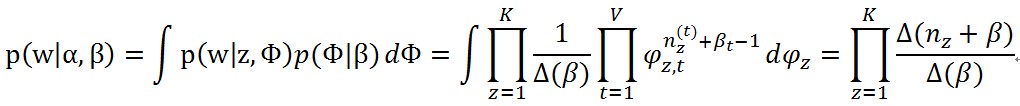
其中是一個V維向量，表示在topic z中，各個詞出現的次數。
從這裡看來，整個語料庫就可以認為文件是K個獨立的多項式分佈生成的。
同樣的，第二個分佈p(z|α)也可以這麼計算，給定了如果給定了一組doc-topic分佈Θ，這個概率可以從語料庫中的每個詞的topic來得到

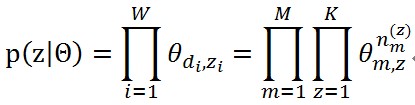
其中di表示第i個詞來自哪個文件，n_(m,z)表示文件m中topic z出現的次數。
把這個概率根據矩陣Θ進行積分，就得到第二個分佈表示了

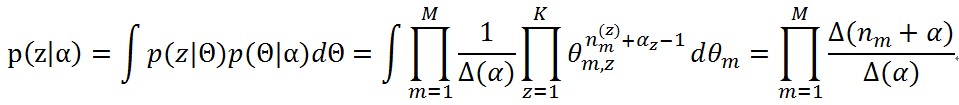
其中是一個K維向量，表示在第m個文件中，各個topic出現的次數。
聯合分佈就變成了
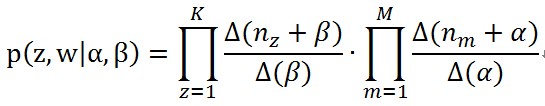     (7)

2.1.3求完全條件分佈

根據上面的公式（7）就能得到Gibbs Sample方法所需要的條件分佈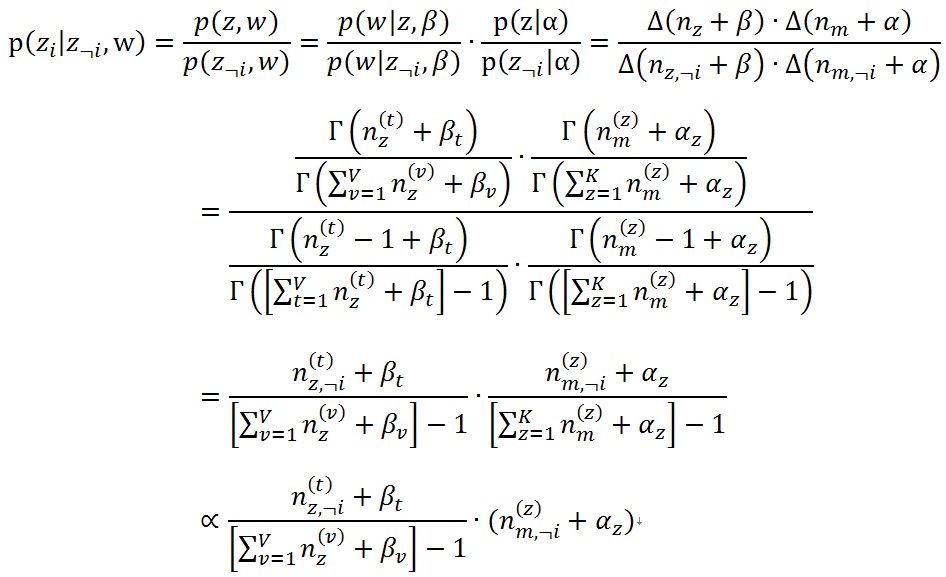
     (8)

其中第一個“=”號的分母，是因為根據（1.2.1）中，一個聯合概率對zi做了積分得到的結果就是沒有這個zi的邊緣分佈。表示這個向量沒有第i列，t表示第t個詞。
1、最後一步那個正比符號出現是因為右下角那一項對所有的zi都一樣，無論有一個詞分配到了那個topic， 都是一樣的，而在Gibbs Sample方法中，同等放大是可以的，所以很多的程式實現都只計算這三項。
2、對於第m篇文件中的第n個詞假設剛好就是語料庫中的第t類詞，它的topic是z，有兩個性質可以使用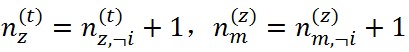。另外。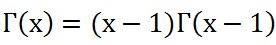
利用這個式子，抽樣就可以進行了。
要注意的是，i是要遍歷整個topic空間的，即i從1到K，需要計算K個概率的。
這裡的步驟就是不斷迭代的，每次迭代都為每個詞抽樣一個新的topic，然後再根據每個詞對應的topic情況估算doc-topic分佈Θ和topic-word分佈Φ。

2.1.4抽樣後更新引數

抽樣後怎麼更新兩個分佈矩陣中的元素呢？
來點推導，對於語料庫中的第i個詞w_i=t，其topic為z_i=k，同時令i=(m,n)，意義為該詞為第m個文件的第n個詞。
回到（1.1.1）中的概率圖，

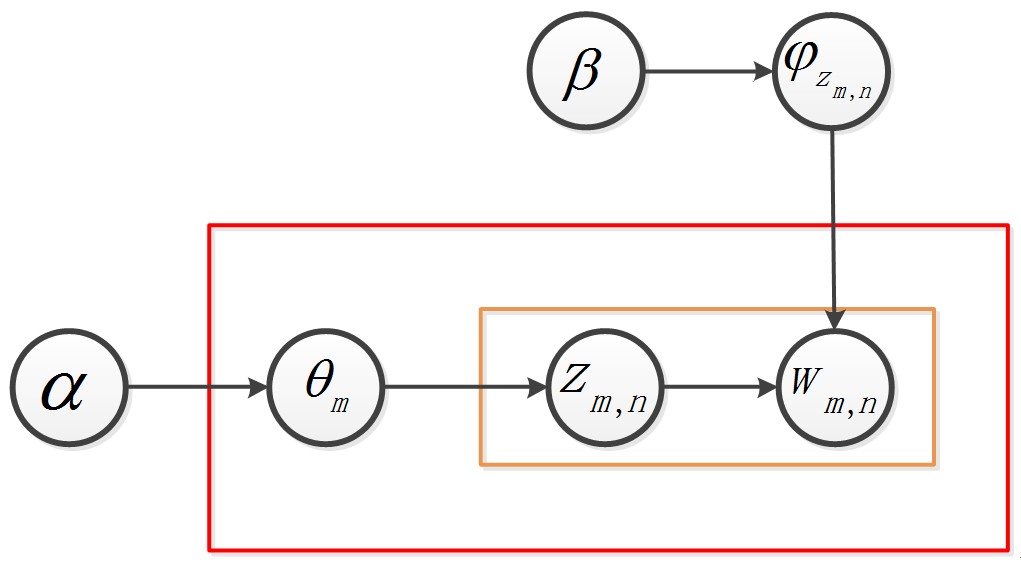
這個概率圖分成兩個物理過程來看：
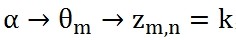，這個過程表示在生成第m 篇文件的時候，先從第一個罈子中抽了一個doc-topic骰子θ_m，然後投擲這個骰子生成了文件中第n個詞的topic編號z_(m,n)=k。
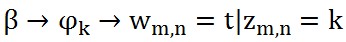，這個過程表示用如下動作生成語料中第m篇文件的第n個詞：在上帝手頭的K個topic-word 骰子Φ中，挑選編號為z_(m,n)=k的那個骰子φ_k進行投擲，然後生成詞w_(m,n)=t。
對於第一個過程來說，α→θ_m→z_m這個過程會生成第m篇文件的所有tipic。《LDA數學八卦》說過，取先驗分佈為Dirichlet分佈，所以前半部分對應於Dirichlet分佈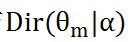，θ_m→z_m就對應於Multinomial 分佈。這樣就構成了一個Dirichlet-Multinomial 共軛結構，如下圖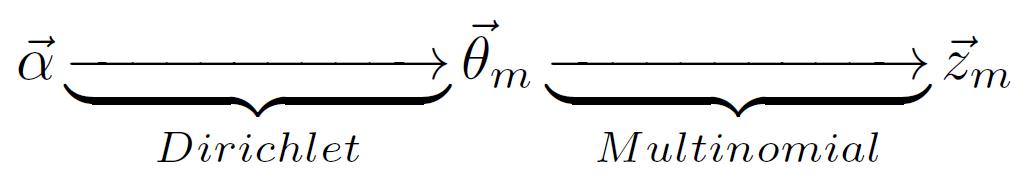

利用這個共軛結構，可以得到引數θ_m的後驗概率是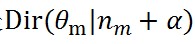，M個文件就有M個這樣的共軛結構，其中n_m是一個K維向量，表示第m個文件中各個topic產生的詞數。
由於LDA是一個bag-of-words結構，各個詞之間都是可以自由交換的。比如說，在第一步中，可以先把所有文件的所有詞的topic先全部生成，再把詞一個個生成。這樣的話，第二步也可以所有相同的topic放在一起，把相應的詞生成。這樣的話，對於topic k中的所有詞來說，這一步就變成了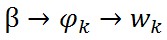，這樣再看，前半部分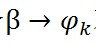對應於Dirichlet分佈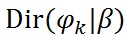，後半部分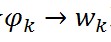對應於Multinomial 分佈，整體構成一個Dirichlet-Multinomial 共軛結構，如下圖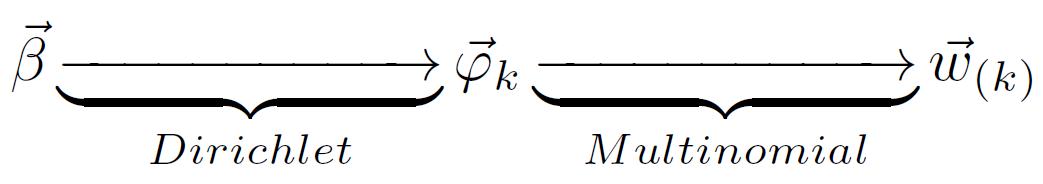

利用這個共軛結構，可以得到引數φ_k的後驗概率是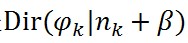，K個topic就有K個這樣的共軛結構，其中n_k是一個V維向量，表示第k個topic中的產生的各個詞的數量。
具體為啥共軛機構會有這樣的效果，具體參看《LDA數學八卦》，裡面說得很清楚了。
根據論文《Parameter estimation for text analysis》中θ_(m,k) 和φ_(k,t) 的定義，計算引數矩陣這兩個值的更新方式如下
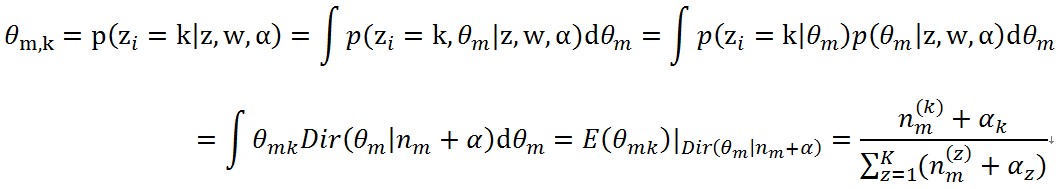    (9)
    (10)
這就得到了更新的式子，但是在實際程式碼中，往往需要在語料庫去掉第i個詞對應的(z_i,w_i)，當然這不會改變分佈的共軛結構，在去掉第i個詞後，更新的式子變成如下的情況了。
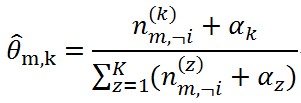    (11)
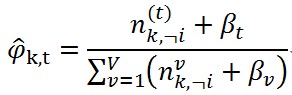    (12)
公式（11），（12）還可以用來在Gibbs Sample方法中計算完全條件分佈(如下
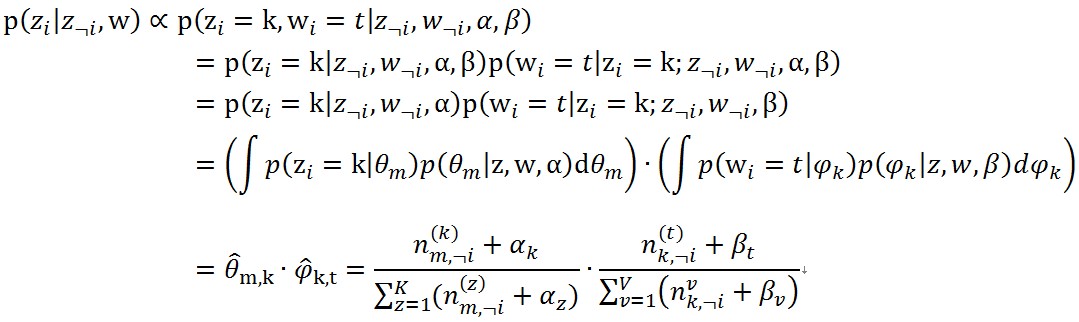    (13)
這種方式就是《LDA數學八卦》選用的方式。
抽樣的過程也要注意的，就是要把一個詞屬於每個topic的概率都計算完了，利用拋繡球的方式抽到了這個詞的一個topic（拋繡球的方式就是：假如topic1的概率是0.2，topic2的概率是0.3，topic3的概率是0.5，那麼就弄10個桶，1號和2號是topic1的，3到5號是topic2的，6到10號是topic3的，產生一個1到10的隨機數（拋的過程），看落到哪個桶就是那個topic）。

2.2 LDA模型整體流程總結

經過上面的討論，各個環節也算是整理了一遍，當然是選用了其他通用的方法，其實在擬合條件概率p(z│w,α,β)的方法也是有其他的，這裡不打算多介紹了。
下面總結一下LDA模型的訓練和推理過程，其實上面那麼多的東西，要做的工作其實是能完成對一篇文件的topic分佈的估算，無論是用判別模型來做，還是生成模型的方法來做，LDA其實就是解決了這麼一個問題。而LDA是一個生成模型，要追溯樣本當初來源的那個分佈，這就導致了各種分佈的擬合與假設，這個方面水比較深，有精力後回來再多解釋。
對於目前文字建模的目標來說，是分兩步的：
就是要根據當前語料庫所有的文件，建立模型，模型建立和選最優往往是伴隨著引數的獲取得到的，就有了各種估計引數的方法；這一步可以稱為訓練過程。
有了最優的引數，模型也建立了，就需要對新來的文件，根據目前的引數，計算這個文件的topic分佈，這一步可以成為預測過程，也就是推理過程。
借用《LDA數學八卦》的東西，這兩步可以用下面的話描述：
估計模型中的兩個引數：doc-topic分佈矩陣Θ={θ_m }_(m=1)^M和topic-word分佈矩陣Φ={φ_k }_(k=1)^K。
對於新來的一篇文件Dnew,能夠計算這篇文件的topic分佈θ_new。

2.2.1 LDA 訓練過程

這個自己就不多寫了，直接從《LDA數學八卦》截個圖吧。

2.2.12LDA 推理過程

訓練過程結束後，得到了引數doc-topic分佈矩陣Θ={θ_m }_(m=1)^M和topic-word分佈矩陣Φ={φ_k }_(k=1)^K。
第一個doc-topic分佈矩陣對於推理來說並沒有用處，在工程上一般不儲存，但是，如果訓練過程就是為了對已有文件進行處理，也可以儲存下來就進行使用的。
第二個topic-word分佈矩陣Φ={φ_k }_(k=1)^K在推理的時候需要用到。來了一個新文件後，根據Gibbs Sampling公式(13)（公式(8)也可以的）為每個詞的topic進行抽樣，最終穩定後就得到了這篇文件的topic分佈θ_new，注意在利用公式（13）計算條件概率的時候，公式中的φ ̂_(k,t)保持不變。
直接從《LDA數學八卦》截個圖吧。

到這，LDA模型基本的東西就完了。

三．未整理的符號說明

以上的符號很多，這裡提供一個未整理的，只能大致應的，來自騰訊廣告的部落格“火光搖曳”。有精力後整理一個本文的吧。

致謝

心懷畏懼@ Crescent，@Rickjin，@AriannaChen，@持之以恆等多位網際網路博主。
機器學習狂熱分子的群友@TK熱心提供的資料。

參考文獻

[1] http://www.crescentmoon.info/?p=296 心懷畏懼@ Crescent的部落格
[2] http://blog.sina.com.cn/s/blog_8eee7fb60101cztv.html @AriannaChen的部落格
[3] http://www.xperseverance.net/blogs/ @持之以恆的部落格
[4] http://www.flickering.cn/nlp/2014/07/lda工程實踐之演算法篇-1演算法實現正確性驗證/ 騰訊廣告的部落格“火光搖曳”
[5] Parameter estimation for text analysis. Gregor Heinrich. Technical Report, 2009.
[6] http://cos.name/2013/03/lda-math-lda-text-modeling 《LDA數學八卦》靳志輝.

[7] Latent Dirichlet Allocation. David M. Blei. Journal of Machine Learning Research 3 (2003) 993-1022

from: http://blog.csdn.net/mytestmy/article/details/39269105