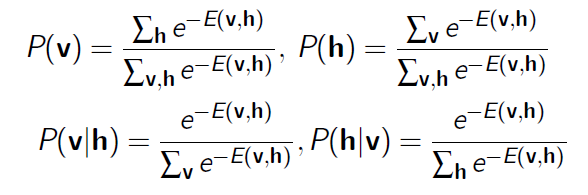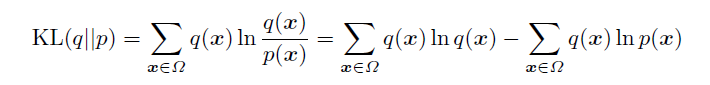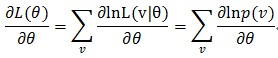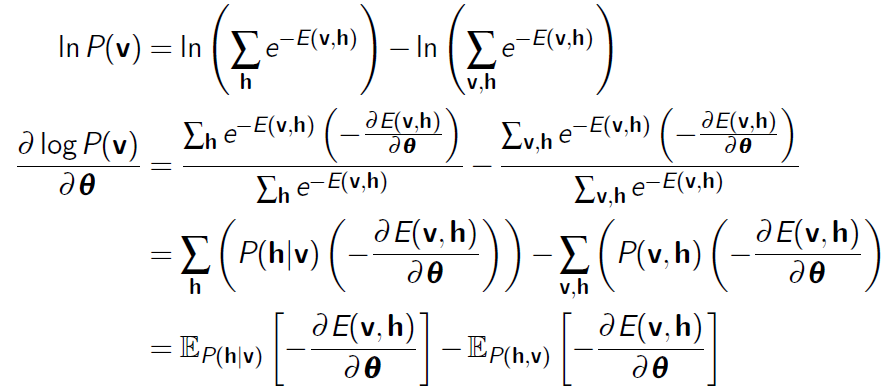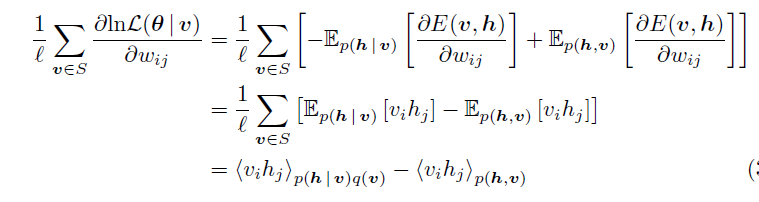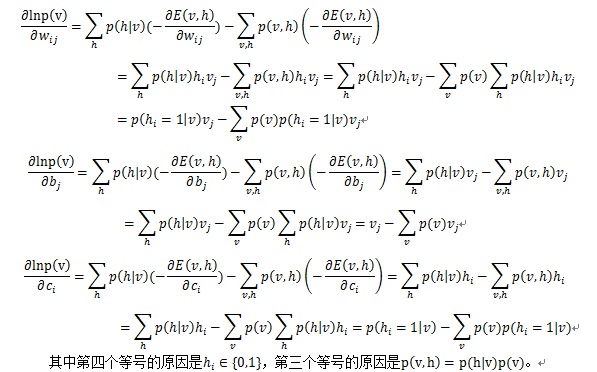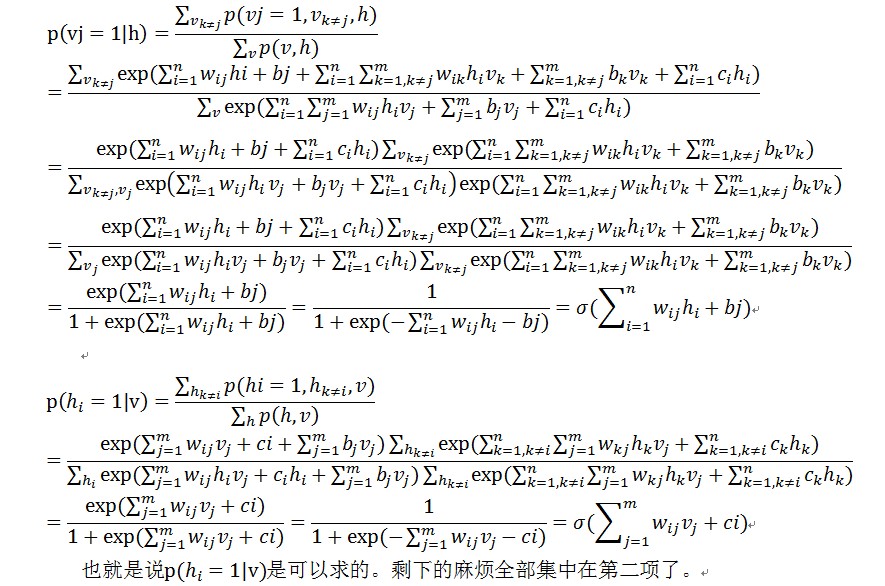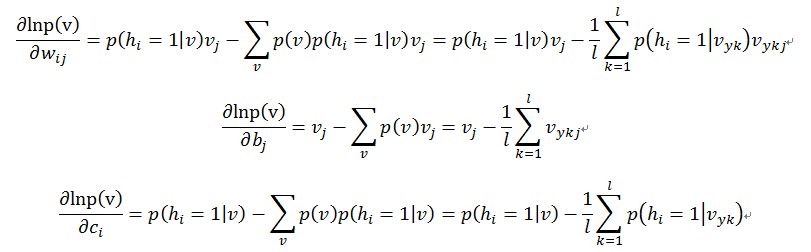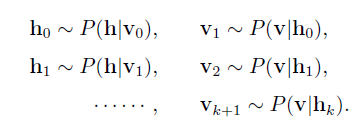深度學習讀書筆記之RBM

garfielder007發表於2016-05-08
深度學習筆記

深度學習讀書筆記之RBM

宣告：

1）看到其他部落格如@zouxy09都有個宣告，老衲也抄襲一下這個東西

2）該博文是整理自網上很大牛和機器學習專家所無私奉獻的資料的。具體引用的資料請看參考文獻。具體的版本宣告也參考原文獻。

3）本文僅供學術交流，非商用。所以每一部分具體的參考資料並沒有詳細對應，更有些部分本來就是直接從其他部落格複製過來的。如果某部分不小心侵犯了大家的利益，還望海涵，並聯系老衲刪除或修改，直到相關人士滿意為止。

4）本人才疏學淺，整理總結的時候難免出錯，還望各位前輩不吝指正，謝謝。

5）閱讀本文需要機器學習、統計學、神經網路等等基礎（如果沒有也沒關係了，沒有就看看，當做跟同學們吹牛的本錢）。

6）此屬於第一版本，若有錯誤，還需繼續修正與增刪。還望大家多多指點。請直接回帖，本人來想辦法處理。

7）由於本人第一次發部落格，連編輯工具都不會用，很多公式就走樣了，只好截圖，格式實在不堪入目，各位前輩有會用發帖工具的可以指點一下。

8）本人手上有word版的和pdf版的，可以到本人csdn資源上面下載，url是：http://download.csdn.net/detail/mytestmy/7246927  資源分是1分，就勞煩各位給老衲積累點下載分了；評論好像可以返還，所以也不讓各位吃虧。



前言

本文較長，請注意要耐心讀。

如果實在不願意耐心讀，起碼看完紅色標誌的句子，不然還得很多問題不清楚。

本文組織的結構比較散，下面是大體過程：

RBM使用方法-->一般用途-->用能量模型的原因-->為什麼要概率以及概率的定義-->求解目標和極大似然的關係-->怎麼求解-->其他的一些補充


一．限制波爾茲曼機

1.1限制波爾茲曼機（RBM）使用方法

1.1.1 RBM的使用說明

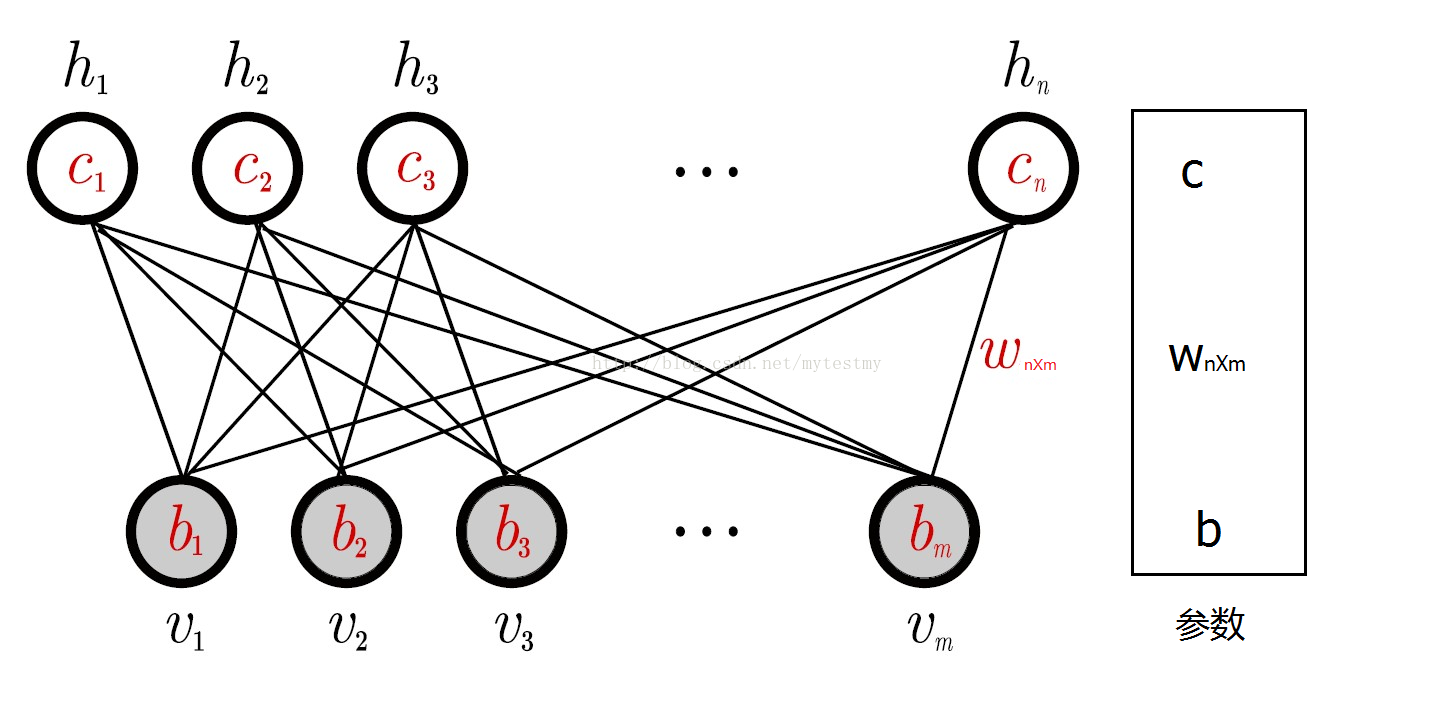
一個普通的RBM網路結構如下。


以上的RBM網路結構有m個可視節點和n個隱藏節點，其中每個可視節點只和n個隱藏節點相關，和其他可視節點是獨立的，就是這個可視節點的狀態只受n個隱藏節點的影響，對於每個隱藏節點也是，只受m個可視節點的影響，這個特點使得RBM的訓練變得容易了。

RBM網路有幾個引數，一個是可視層與隱藏層之間的權重矩陣{W_{n \times m}}，一個是可視節點的偏移量b=(b1,b2⋯bm)，一個是隱藏節點的偏移量c=(c1,c2⋯cn)，這幾個引數決定了RBM網路將一個m維的樣本編碼成一個什麼樣的n維的樣本。

RBM網路的功能有下面的幾種，就簡單地先描述一下。
首先為了描述容易，先假設每個節點取值都在集合{0,1}中，即\forall {\rm{i}},{\rm{j}},{v_j} \in \left\{ {0,1} \right\},{h_i} \in \left\{ {0,1} \right\}。

一個訓練樣本x過來了取值為x=(x1,x2⋯xm)，根據RBM網路，可以得到這個樣本的m維的編碼後的樣本y=(y1,y2⋯yn)，這n維的編碼也可以認為是抽取了n個特徵的樣本。而這個m維的編碼後的樣本是按照下面的規則生成的：對於給定的x=(x1,x2⋯xm)，隱藏層的第i個節點的取值為1（編碼後的樣本的第i個特徵的取值為1）的概率為{\rm{p}}\left( {{\rm{hi}} = 1{\rm{|v}}} \right) = {\rm{\sigma }}\left( { \sum \limits_{j = 1}^m wij \times {\rm{vj}} + {\rm{ci}}} \right)，其中的v取值就是x，hi的取值就是yi，其中{\rm{\sigma }}\left( {\rm{x}} \right) = 1/\left( {1 + {e^{ - x}}} \right)，是sigmoid函式。也就是說，編碼後的樣本y的第i個位置的取值為1的概率是p(hi=1|v)。所以，生成yi的過程就是：
i）先利用公式{\rm{p}}\left( {{\rm{hi}} = 1{\rm{|v}}} \right) = {\rm{\sigma }}\left( { \sum \limits_{j = 1}^m wij \times {\rm{vj}} + {\rm{ci}}} \right)，根據x的值計算概率p(hi=1|v)，其中vj的取值就是xj的值。
ii）然後產生一個0到1之間的隨機數，如果它小於p(hi=1|v)，yi的取值就是1，否則就是0（假如p(hi=1|v)=0.6，這裡就是因為yi的取值就是1的概率是,0.6，而這個隨機數小於0.6的概率也是0.6；如果這個隨機數小於0.6，就是這個事件發生了，那就可以認為yi的取值是1這個事件發生了，所以把yi取值為1）。
反過來，現在知道了一個編碼後的樣本y，想要知道原來的樣本x，即解碼過程，跟上面也是同理，過程如下：
i）先利用公式{\rm{p}}\left( {{\rm{vj}} = 1{\rm{|h}}} \right) = {\rm{\sigma }}\left( { \sum \limits_{i = 1}^n wij \times {\rm{hi}} + {\rm{bj}}} \right)，根據y的值計算概率p(vj=1|h)，其中hi的取值就是yi的值。
ii）然後按照均勻分佈產生一個0到1之間的隨機浮點數，如果它小於p(vj=1|h)，vj的取值就是1，否則就是0。

對於（ii）的說明：不說別的——比如吧，你現在出去逛街，走到一個岔路口，你只想隨便逛逛，所以你是有0.5的概率往左邊的路，0.5的概率往右邊的路；但是你不知道怎麼選擇哪個路，所以你選擇了拋硬幣，正面朝上你就向左，反面朝上就向右。現在你只拋一次，發現他是正面朝上的，你就向左走了。

——回到上面的問題，某節點A取值為1的概率是0.6（假如），也可以看做一個找不均勻的硬幣，正面朝上的概率是0.6，反面朝上的概率是0.4；現在要給節點A取值，就拿這個硬幣拋一下，正面朝上就取值1，反面朝上就取值0，這個就相當於拋硬幣決定走哪個路的那個過程。

——現在假如找不到這樣的不均勻的硬幣，就拿隨機數生成器來代替（生成的數是0-1之間的浮點數）；因為隨機數生成器取值小於0.6的概率也是0.6，大於0.6的概率是0.4。



1.1.2 RBM的用途

RBM的用途主要是兩種，一是對資料進行編碼，然後交給監督學習方法去進行分類或迴歸，二是得到了權重矩陣和偏移量，供BP神經網路初始化訓練。

第一種可以說是把它當做一個降維的方法來使用。

第二種就用途比較奇怪。其中的原因就是神經網路也是要訓練一個權重矩陣和偏移量，但是如果直接用BP神經網路，初始值選得不好的話，往往會陷入區域性極小值。根據實際應用結果表明，直接把RBM訓練得到的權重矩陣和偏移量作為BP神經網路初始值，得到的結果會非常地好。

這就類似爬山，如果一個風景點裡面有很多個山峰，如果讓你隨便選個山就爬，希望你能爬上最高那個山的山頂，但是你的精力是有限的，只能爬一座山，而你也不知道哪座山最高，這樣，你就很容易爬到一座不是最高的山上。但是，如果用直升機把你送到最高的那個山上的靠近山頂處，那你就能很容易地爬上最高的那座山。這個時候，RBM就的角色就是那個直升機。

其實還有兩種用途的，下面說說。

第三種，RBM可以估計聯合概率p(v,h)，如果把v當做訓練樣本，h當成類別標籤（隱藏節點只有一個的情況，能得到一個隱藏節點取值為1的概率），就可以利用利用貝葉斯公式求p(h|v)，然後就可以進行分類，類似樸素貝葉斯、LDA、HMM。說得專業點，RBM可以作為一個生成模型（Generative model）使用。

第四種，RBM可以直接計算條件概率p(h|v)，如果把v當做訓練樣本，h當成類別標籤（隱藏節點只有一個的情況，能得到一個隱藏節點取值為1的概率），RBM就可以用來進行分類。說得專業點，RBM可以作為一個判別模型（Discriminative model）使用。



1.2限制波爾茲曼機（RBM）能量模型

1.2.1 能量模型定義

在說RBM之前，先來說點其他的，就是能量模型。

能量模型是個什麼樣的東西呢？直觀上的理解就是，把一個表面粗糙又不太圓的小球，放到一個表面也比較粗糙的碗裡，就隨便往裡面一扔，看看小球停在碗的哪個地方。一般來說停在碗底的可能性比較大，停在靠近碗底的其他地方也可能，甚至運氣好還會停在碗口附近（這個碗是比較淺的一個碗）；能量模型把小球停在哪個地方定義為一種狀態，每種狀態都對應著一個能量，這個能量由能量函式來定義，小球處在某種狀態的概率（如停在碗底的概率跟停在碗口的概率當然不一樣）可以通過這種狀態下小球具有的能量來定義（換個說法，如小球停在了碗口附近，這是一種狀態，這個狀態對應著一個能量E，而發生“小球停在碗口附近”這種狀態的概率p，可以用E來表示，表示成p=f(E)，其中f是能量函式），這就是我認為的能量模型。

這樣，就有了能量函式，概率之類的東西。

波爾茲曼網路是一種隨機網路。描述一個隨機網路，總結起來主要有兩點。

第一，概率分佈函式。由於網路節點的取值狀態是隨機的，從貝葉斯網的觀點來看，要描述整個網路，需要用三種概率分佈來描述系統。即聯合概率分佈，邊緣概率分佈和條件概率分佈。要搞清楚這三種不同的概率分佈,是理解隨機網路的關鍵,這裡向大家推薦的書籍是張連文所著的《貝葉斯網引論》。很多文獻上說受限波爾茲曼是一個無向圖，從貝葉斯網的觀點看，受限波爾茲曼網路也可以看作一個雙向的有向圖，即從輸入層節點可以計算隱層節點取某一種狀態值的概率，反之亦然。

第二，能量函式。隨機神經網路是根植於統計力學的。受統計力學中能量泛函的啟發，引入了能量函式。能量函式是描述整個系統狀態的一種測度。系統越有序或者概率分佈越集中，系統的能量越小。反之，系統越無序或者概率分佈越趨於均勻分佈，則系統的能量越大。能量函式的最小值，對應於系統的最穩定狀態。

1.2.2 能量模型作用

為什麼要弄這個能量模型呢？原因有幾個。

第一、RBM網路是一種無監督學習的方法，無監督學習的目的是最大可能的擬合輸入資料，所以學習RBM網路的目的是讓RBM網路最大可能地擬合輸入資料。

第二、對於一組輸入資料來說，現在還不知道它符合那個分佈，那是非常難學的。例如，知道它符合高斯分佈，那就可以寫出似然函式，然後求解，就能求出這個是一個什麼樣個高斯分佈；但是要是不知道它符合一個什麼分佈，那可是連似然函式都沒法寫的，問題都沒有，根本就無從下手。

好在天無絕人之路——統計力學的結論表明，任何概率分佈都可以轉變成基於能量的模型，而且很多的分佈都可以利用能量模型的特有的性質和學習過程，有些甚至從能量模型中找到了通用的學習方法。有這樣一個好東西，當然要用了。

第三、在馬爾科夫隨機場（MRF）中能量模型主要扮演著兩個作用：一、全域性解的度量（目標函式）；二、能量最小時的解（各種變數對應的配置）為目標解。也就是能量模型能為無監督學習方法提供兩個東西：a）目標函式；b）目標解。

換句話說，就是——使用能量模型使得學習一個資料的分佈變得容易可行了。

能否把最優解嵌入到能量函式中至關重要，決定著我們具體問題求解的好壞。統計模式識別主要工作之一就是捕獲變數之間的相關性，同樣能量模型也要捕獲變數之間的相關性，變數之間的相關程度決定了能量的高低。把變數的相關關係用圖表示出來，並引入概率測度方式就構成了概率圖模型的能量模型。

RBM作為一種概率圖模型，引入了概率就可以使用取樣技術求解，在CD（contrastive divergence）演算法中取樣部分扮演著模擬求解梯度的角色。

能量模型需要一個定義能量函式，RBM的能量函式的定義如下

{\rm{E}}\left( {{\rm{v}},{\rm{h}}} \right) = - \sum \limits_{i = 1}^n \sum \limits_{j = 1}^m {w_{ij}}{h_i}{v_j} - \sum \limits_{j = 1}^m {b_j}{v_j} - \sum \limits_{i = 1}^n {c_i}{h_i}

這個能量函式的意思就是，每個可視節點和隱藏節點之間的連線結構都有一個能量，通俗來說就是可視節點的每一組取值和隱藏節點的每一組取值都有一個能量，如果可視節點的一組取值（也就是一個訓練樣本的值）為(1,0,1,0,1,0)，隱藏節點的一組取值（也就是這個訓練樣本編碼後的值）為(1,0,1)，然後分別代入上面的公式，就能得到這個連線結構之間的能量。


能量函式的意義是有一個解釋的，叫做專家乘積系統（POE，product of expert），這個理論也是hinton發明的，他把每個隱藏節點看做一個“專家”，每個“專家”都能對可視節點的狀態分佈產生影響，可能單個“專家”對可視節點的狀態分佈不夠強，但是所有的“專家”的觀察結果連乘起來就夠強了。具體我也看不太懂，各位有興趣看hinton的論文吧，中文的也有，叫《專家乘積系統的原理及應用，孫徵，李寧》。

另外的一個問題是：為什麼要搞概率呢？下面就是解釋。

能量模型需要兩個東西，一個是能量函式，另一個是概率，有了概率才能跟要求解的問題聯合起來。

下面就介紹從能量模型到概率吧。

1.3從能量模型到概率

1.3.1 從能量函式到概率

為了引入概率，需要定義概率分佈。根據能量模型，有了能量函式，就可以定義一個可視節點和隱藏節點的聯合概率

{\rm{p}}\left( {{\rm{v}},{\rm{h}}} \right) = \frac{{{e^{ - E\left( {v,h} \right)}}}}{{ \sum \nolimits_{v,h} {e^{ - E\left( {v,h} \right)}}}}

也就是一個可視節點的一組取值（一個狀態）和一個隱藏節點的一組取值（一個狀態）發生的概率p(v,h)是由能量函式來定義的。

這個概率不是隨便定義的，而是有統計熱力學的解釋的——在統計熱力學上，當系統和它周圍的環境處於熱平衡時，一個基本的結果是狀態i發生的概率如下面的公式

{{\rm{p}}_i} = \frac{1}{Z} \times {e^{ - \frac{{{E_i}}}{{{k_b} \times T}}}}

其中表示系統在狀態i時的能量，T為開爾文絕對溫度，為Boltzmann常數，Z為與狀態無關的常數。

我們這裡的變成了E(v,h)，因為(v,h)也是一個狀態，其他的引數T和由於跟求解無關，就都設定為1了，Z就是我們上面聯合概率分佈的分母，這個分母是為了讓我們的概率的和為1，這樣才能保證p(v,h)是一個概率。

現在我們得到了一個概率，其實也得到了一個分佈，其實這個分佈還有一個好聽點的名字，可以叫做Gibbs分佈，當然不是一個標準的Gibbs分佈，而是一個特殊的Gibbs分佈，這個分佈是有一組引數的，就是能量函式的那幾個引數w，b，c。

有了這個聯合概率，就可以得到一些條件概率，是用積分去掉一些不想要的量得到的。


1.3.2 從概率到極大似然

上面得到了一個樣本和其對應編碼的聯合概率，也就是得到了RBM網路的Gibbs分佈的概率密度函式，引入能量模型的目的是為了方便求解的。

現在回到求解的目標——讓RBM網路的表示Gibbs分佈最大可能的擬合輸入資料。

其實求解的目標也可以認為是讓RBM網路表示的Gibbs分佈與輸入樣本的分佈儘可能地接近。

現在看看“最大可能的擬合輸入資料”這怎麼定義。

假設Ω表示樣本空間，q是輸入樣本的分佈，即q(x)表示訓練樣本x的概率， q其實就是要擬合的那個樣本表示分佈的概率；再假設p是RBM網路表示的Gibbs分佈的邊緣分佈（只跟可視節點有關，隱藏節點是通過積分去掉了，可以理解為可視節點的各個狀態的分佈），輸入樣本的集合是S，那現在就可以定義樣本表示的分佈和RBM網路表示的邊緣分佈的KL距離


如果輸入樣本表示的分佈與RBM表示的Gibbs分佈完全符合，這個KL距離就是0，否則就是一個大於0的數。

第一項其實就是輸入樣本的熵（熵的定義），輸入樣本定了熵就定了；第二項沒法直接求，但是如果用蒙特卡羅抽樣（後面有章節會介紹），讓抽中的樣本是輸入樣本（輸入樣本肯定符合分佈q(x)），第二項可以用\frac{1}{l} \sum \limits_{x \in S} {\rm{ln}}p\left( x \right)來估計，其中的l表示訓練樣本個數。由於KL的值肯定是不小於0，所以第一項肯定不小於第二項，讓第二項取得最大值，就能讓KL距離最小；最後，還可以發現，最大化\frac{1}{l} \sum \limits_{x \in S} {\rm{ln}}p\left( x \right)，相當於最大化\sum \limits_{x \in S} {\rm{ln}}p\left( x \right)，而這就是極大似然估計。

結論就是求解輸入樣本的極大似然，就能讓RBM網路表示的Gibbs分佈和樣本本身表示的分佈最接近。

這就是為什麼RBM問題最終可以轉化為極大似然來求解。

既然要用極大似然來求解，這個當然是有意義的——當RBM網路訓練完成後，如果讓這個RBM網路隨機發生若干次狀態（當然一個狀態是由(v,h)組成的），這若干次狀態中，可視節點部分（就是v）出現訓練樣本的概率要最大。

這樣就保證了，在反編碼（從隱藏節點到可視節點的編碼過程）過程中，能使訓練樣本出現的概率最大，也就是使得反編碼的誤差盡最大的可能最小。

例如一個樣本(1,0,1,0,1)編碼到(0,1,1)，那麼，(0,1,1)從隱藏節點反編碼到可視節點的時候也要大概率地編碼到(1,0,1,0,1)。

到這，能量模型到極大似然的關係說清楚了，，可能有點不太對，大家看到有什麼不對的提一下，我把它改了。

之前想過用似然函式最大的時候，RBM網路的能量最小這種思路去解釋，結果看了很多的資料，都實在沒有辦法把那兩個極值聯絡起來。這個冤枉路走了好久，希望大家在學習的時候多注意，儘量避免走這個路。

下面就說怎麼求解了。求解的意思就是求RBM網路裡面的幾個引數w，b，c的值，這個就是解，而似然函式（對數似然函式）是目標函式。最優化問題裡面的最優解和目標函式的關係大家務必先弄清楚。


1.4求解極大似然

既然是求解極大似然，就要對似然函式求最大值，

求解的過程就是對引數就導，然後用梯度上升法不斷地把目標函式提升，最終到達停機條件（在這裡看不懂的同學就去看參考文獻中的《從極大似然到EM》），

設引數為（注意是引數是一組引數），則似然函式可以寫為

{\rm{L}}\left( {\rm{\theta }} \right) = \prod \limits_v {\rm{L}}\left( {{\rm{v|\theta }}} \right) = \prod \limits_v p\left( v \right)

為了省事L(v│θ)=p(v|θ)寫成p(v)了,然後就可以對它的對數進行求導了（因為直接求一個連乘的導數太複雜，所以變成對數來求）


    可以看到，是對每個p(v)求導後再加和，然後就有了下面的推導了。

到了這一步的時候，我們又可以發現問題了。我們可以看到的是，對每一個樣本，第二個等號後面的兩項其實都像是在求一個期望，第一項求的是- \frac{{\partial {\rm{E}}\left( {{\rm{v}},{\rm{h}}} \right)}}{{\partial \theta }}這個函式在概率p(h|v)下的期望，第二項求的是- \frac{{\partial {\rm{E}}\left( {{\rm{v}},{\rm{h}}} \right)}}{{\partial \theta }}這個函式在概率p(v,h)下面的期望。
還有論文是這麼解釋的，上面的公式，對w求偏導，還可以再進一步轉化


注意：從第二個“=”號到第三個“=”號的時候，第二個“=”號的方括號裡面的第一項是把蒙特卡羅抽樣的用法反過來了，從抽樣回到了積分，所以得到了一個期望；第二項就是因為對每個訓練樣本，第二項的值算出來都一樣，所以累加以後的結果除以l，相當於沒有變化，還是那個期望，只是表達的形式換了。

這樣的話，這個梯度還可以這麼理解，第一項等於輸入樣本資料的自由能量函式偏導在樣本本身的那個分佈下的期望值（q(v,h)=p(h|v)q(v)，q表示輸入樣本和他們對應的隱藏增狀態表示的分佈），而第二項是自由能量函式的偏導在RBM網路表示的Gibbs分佈下的期望值。

第一項是可以求的，因為訓練樣本有了，也就是使用蒙特卡羅估算期望的時候需要的樣本已經抽好了，只要求個均值就可以了。

第二項也是可以求的，但是要對v和h的組合的所有可能的取值都遍歷一趟，這就可能沒法算了；想偷懶的話，悲劇就在於，現在是沒有RBM網路表示的Gibbs分佈下的樣本的（當然後面會介紹這些怎麼抽）。

為了進行下面的討論，把這個梯度再進一步化簡，看看能得到什麼。根據能量函式的公式，是有三個引數的w，b和c，就分別對這三個引數求導



到了這一步，來分析一下，從上面的聯合概率那一堆，我們可以得到下面的


要求第二項，就要遍歷所有可能的v的值，然後根據公式去計算幾個梯度的值，那樣夠麻煩的了，還好蒙特卡羅給出了一個偷懶的方法，見後面的章。

只要抽取一堆樣本，這些樣本符合RBM網路表示的Gibbs分佈的（也就是符合引數確定的Gibbs分佈p(x)的），就可以把上面的三個偏導數估算出來。

對於上面的情況，是這麼處理的，對每個訓練樣本x，都用某種抽樣方法抽取一個它對應的符合RBM網路表示的Gibbs分佈的樣本（對應的意思就是符合引數確定的Gibbs分佈p(x)的），假如叫y；那麼，對於整個的訓練集{x1,x2,…xl}來說，就得到了一組符合RBM網路表示的Gibbs分佈的樣本{y1,y2,…,yl}，然後拿這組樣本去估算第二項，那麼梯度就可以用下面的公式來近似了


其中xk表示第k個訓練樣本，yk表示第k個訓練樣本對應的RBM網路表示的Gibbs分佈（不妨將這個分佈稱為R）的樣本（yk是根據分佈R抽取的樣本，而且這個樣本是從xk出發，用Gibbs抽樣抽取出來的，也就是說yk服從分佈R，可以用來估算第二項，同時yk跟xk有關），Vyk表示可視節點取值為yk的時候的狀態，那麼Vykj就表示yk的第j個特徵的取值。

這樣，梯度出來了，這個極大似然問題可以解了，最終經過若干論迭代，就能得到那幾個引數w，b，c的解。

式子中的v是指{x1,x2,…xl}中的一個樣本，因為\frac{{\partial {\rm{lnL}}({\rm{\theta }}|{\rm{v}})}}{{\partial \theta }} = \sum \limits_v \frac{{\partial {\rm{ln}}p\left( v \right)}}{{\partial \theta }}，對樣本進行累加時，第一項是對所有樣本進行累加，而第二項都是一樣的（是一個積分的結果，與被積變數無關，是一個標量），所以累加後1/l就沒有了，只有對l項y進行累加，到了下面CD-k演算法的時候，每次只對一個x和一個y進行處理，最外層對x做L次迴圈後得到的累加結果是一樣的.
上面提到的“某種抽樣方法”，現在一般就用Gibbs抽樣，然後hinton教授還根據這個弄出了一個CD-k演算法，就是用來解決RBM的抽樣的。下面一章就介紹這個吧。


1.5用到的抽樣方法

一般來說，在hinton教授還沒弄出CD-k之前，解決RBM的抽樣問題是用Gibbs抽樣的。

Gibbs抽樣是一種基於馬爾科夫蒙特卡羅（Markov Chain Monte Carlo,MCMC）策略的抽樣方法。具體就是，對於一個d維的隨機向量x=(x1,x2,…xd)，假設我們無法求得x的聯合概率分佈p(x)，但我們知道給定x的其他分量是，其第i個分量xi的條件分佈，即p(xi|xi-),xi-=(x1,x2,…xi-1,xi+1…xd)。那麼，我們可以從x的一個任意狀態（如(x1(0),x2(0),…,xd(0))）開始，利用條件分佈p(xi|xi-)，迭代地對這狀態的每個分量進行抽樣，隨著抽樣次數n的增加，隨機變數(x1(n),x2(n),…,xd(n))的概率分佈將以n的幾何級數的速度收斂與x的聯合概率分佈p(v)。

Gibbs抽樣其實就是可以讓我們可以在位置聯合概率分佈p(v)的情況下對其進行抽樣。

基於RBM模型的對稱結構，以及其中節點的條件獨立行，我們可以使用Gibbs抽樣方法得到服從RBM定義的分佈的隨機樣本。在RBM中進行k步Gibbs抽樣的具體演算法為：用一個訓練樣本（或者可視節點的一個隨機初始狀態）初始化可視節點的狀態v0，交替進行下面的抽樣：


在抽樣步數n足夠大的情況下，就可以得到RBM所定義的分佈的樣本（即符合引數確定的Gibbs分佈的樣本）了，得到這些樣本我們就可以拿去計算梯度的第二項了。

可以看到，上面進行了k步的抽樣，這個k一般還要比較大，所以是比較費時間的，尤其是在訓練樣本的特徵數比較多（可視節點數大）的時候，所以hinton教授就弄一個簡化的版本，叫做CD-k，也就對比散度。

對比散度是英文ContrastiveDivergence（CD）的中文翻譯。與Gibbs抽樣不同，hinton教授指出當使用訓練樣本初始化v0的時候，僅需要較少的抽樣步數（一般就一步）就可以得到足夠好的近似了。

在CD演算法一開始，可見單元的狀態就被設定為一個訓練樣本，並用上面的幾個條件概率來對隱藏節點的每個單元都從{0,1}中抽取到相應的值，然後再利用 來對可視節點的每個單元都從{0,1}中抽取相應的值，這樣就得到了v1了，一般v1就夠了，就可以拿來估算梯度了。

下面給出RBM的基於CD-k的快速學習的主要步驟。


其中，之所以第二項沒有了那個1/l，就是因為這個梯度會對所有樣本進行累加（極大似然是所有訓練樣本的梯度的和），最終加和的結果跟現在這樣算是相等的（剛好是l個樣本，l個第二項相加後，最終結果剛好等於每一個第二項的那個累加符號後面的那一項，而這裡所有結果加和後，也能得到相同的值）。

1.6馬爾科夫蒙特卡羅簡介

下面簡介一下馬爾科夫蒙特卡羅（MCMC）方法。

最早的蒙特卡羅方法，是由物理學家發明的，旨在於通過隨機化的方法計算積分。假設給定函式h(x)，我們想計算積分\smallint \limits_{\rm{a}}^b h\left( x \right)dx，但是又沒有辦法對區間內的所有x的取值都算一遍，我們可以將h(x)分解為某個函式f(x)和一個定義在(a, b)上的概率密度函式p(x)的乘積。這樣整個積分就可以寫成：
\smallint \limits_{\rm{a}}^b h\left( x \right)dx = \smallint \limits_a^b f\left( x \right)p\left( x \right)dx = {E_{p\left( x \right)}}\left[ {f\left( x \right)} \right]

這樣一來，原積分就等同於f(x)在p(x)這個分佈上的均值(期望)。這時，如果我們從分佈p(x)上採集大量的樣本x1, x2, ..., xn，這些樣本符合分佈p(x)，即\forall {\rm{i}},{x_i}/ \sum \limits_i {x_i} \approx p\left( {{x_i}} \right)，那麼，我們就可以通過這些樣本來逼近這個均值：
\smallint \limits_a^{\rm{b}} h\left( x \right)dx = {E_{p\left( x \right)}}\left[ {f\left( x \right)} \right] = \frac{1}{n} \sum \limits_{i = 1}^n f\left( {{x_i}} \right)
這就是蒙特卡羅方法的基本思想。
然後剩下的就是怎麼樣能夠取樣到符合分佈p(x)的樣本了，這個簡單來說就是一個隨機的初始樣本，通過馬爾科夫鏈進行多次轉移，最終就能得到符合分佈p(x)的樣本。上面介紹的Gibbs是一種比較常用的抽樣演算法。
有關Gibbs抽樣的相關內容可以參看文獻【12】。
這就是蒙特卡羅方法的基本思想。

然後剩下的就是怎麼樣能夠取樣到符合分佈p(x)的樣本了，這個簡單來說就是一個隨機的初始樣本，通過馬爾科夫鏈進行多次轉移，最終就能得到符合分佈p(x)的樣本。上面介紹的Gibbs是一種比較常用的抽樣演算法。

有關Gibbs抽樣的相關內容可以參看文獻【12】。



致謝

Deep Learning高質量交流群裡的多位同學：@zeonsunlight，@marvin，@tornadomeet，@好久不見，@zouxy09

他們在我寫這個筆記的過程中提供了多方面的資料。

特別是：@ zeonsunlight，幫助我弄清楚了很多概念；@好久不見，幫我改正了部落格中的符號的錯誤。

本人愚鈍，多數問題都需要各位同學的多次點撥，在此向他們表示衷心的感謝。

這個筆記的其他方面介紹，我覺得都算清楚，唯獨在說能量模型的時候，感覺是沒把能量模型介紹清楚，有懂的前輩希望能指導一下。

最後，還是得說，本人才疏學淺，肯定有大量的錯誤，希望大家能多多包涵並且指出，讓我能及時改正。


參考文獻



[1] An Introduction to Restricted Boltzmann Machines.Asja Fischer andChristian Igel

[2] 受限波爾茲曼機簡介 張春霞，姬楠楠，王冠偉

[3] LearningDeep Architectures for AI  Yoshua Bengio

[4] http://blog.csdn.net/cuoqu/article/details/8886971 DeepLearning（深度學習）原理與實現（一）@marvin521

[5] http://blog.csdn.net/zouxy09/article/details/8775360  Deep Learning（深度學習）學習筆記整理系列 @zouxy09

[6] http://www.cnblogs.com/tornadomeet/archive/2013/03/27/2984725.html    Deep learning：十九(RBM簡單理解) @tornadomeet

[7] http://blog.csdn.net/celerychen2009/article/details/8984316    受限波爾茲曼機  @celerychen2009

[8] http://blog.csdn.net/zouxy09/article/details/8537620    從最大似然到EM演算法淺解   @zouxy09

[9] http://www.sigvc.org/bbs/thread-513-1-3.html 《RBM 和DBN 的訓練》 王穎

[10]  神經網路原理葉[M] 葉世偉，史忠植：機械工業出版社

[11] http://www.sigvc.org/bbs/thread-512-1-1.html  《Restricted BoltzmannMachine (RBM) 推導》朱飛雲

[12] http://www.52nlp.cn/lda-math-mcmc-%E5%92%8C-gibbs-sampling1gibbs抽樣相關


from: http://blog.csdn.net/mytestmy/article/details/9150213

相關文章