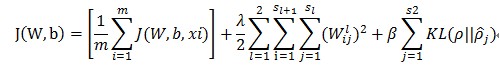深度學習讀書筆記之AE（自動編碼AutoEncoder）

garfielder007發表於2016-05-08
深度學習筆記

深度學習讀書筆記之AE

宣告：

1）該博文是整理自網上很大牛和機器學習專家所無私奉獻的資料的。具體引用的資料請看參考文獻。具體的版本宣告也參考原文獻。

2）本文僅供學術交流，非商用。所以每一部分具體的參考資料並沒有詳細對應，而且大部分內容都是直接抄NG的源部落格的，如果某部分不小心侵犯了大家的利益，還望海涵，並聯系老衲刪除或修改，直到相關人士滿意為止。

3）本人才疏學淺，整理總結的時候難免出錯，還望各位前輩不吝指正，謝謝。

4）閱讀本文需要機器學習、統計學、神經網路等等基礎（如果沒有也沒關係了，沒有就看看，當做跟同學們吹牛的本錢）。

5）此屬於第一版本，若有錯誤，還需繼續修正與增刪。還望大家多多指點。請直接回帖，本人來想辦法處理。

6）本人手上有word版的和pdf版的，不知道怎麼上傳，所以需要的話可以直接到DeepLearning高質量交流群裡要，群號由於未取得群主同意不敢公佈，需要的同學可以聯絡群主@tornadomeet


一．稀疏自編碼器

1.1一般AE使用方法

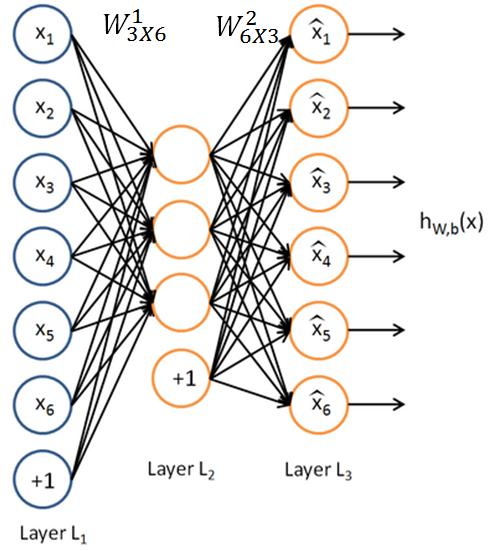
下圖是一個自編碼神經網路的示例。

上面是一個三層的自編碼神經網路，分別有L1，L2，L3這三層。
網路經過學習以後，得到的結果是兩個矩陣和兩個偏移量，W_{3 \times 6}^1和偏移量b1、{\rm{W}}_{6 \times 3}^2和b2。
給定輸入x=(x1,x2,x3,x4,x5,x6)，根據已知的啟用函式f1,f2，這兩個矩陣和偏移量有如下的性質：
令{\rm{yi}} = {\rm{f}}1\left( { \sum \limits_{j = 1}^6 w_{ij}^1 \times {\rm{x}}j + b_i^1} \right)，從而得到y=(y1,y2,y3)，其中f1是sigmoid函式，形式 

f(z) = \frac{1}{{1 + \exp ( - z)}}
再令{\rm{zi}} = {\rm{f}}2\left( { \sum \limits_{j = 1}^3 w_{ij}^2 \times {\rm{yj}} + b_i^2} \right),從而得到z=(z1,z2,z3,z4,z5,z6)其中f2是自等函式，形式f(z)=z.如果輸入資料在0和1之間，也可以用f1是sigmoid函式。
一個訓練得很好的自編碼神經網路滿足x=z。

1.2自編碼AE的意義

只對影象進行解釋。
假如是一個L1層10000個節點，L2層100個節點，L3層10000個節點的AE網路，同時所有啟用函式選用sigmoid函式，那麼W_{100X10000}^1，
用大量的圖片訓練得到W_{100X10000}^1，{\rm{W}}_{10000 \times 100}^2；對於W_{100X10000}^1的每一行，把W_{100X10000}^1的權重用公式{{\rm{x}}_{\rm{j}}} = \frac{{{\rm{W}}_{{\rm{ij}}}^1}}{{\sqrt { \sum \nolimits_{{\rm{j}} = 1}^{10000} {{\left( {{\rm{W}}_{{\rm{ij}}}^1} \right)}^2}} }}，得到的x=(x1,x2,⋯,x10000)，組合成一幅100*100的子圖，就能得到100幅子圖，都是一些邊緣，如下面的這些

可以看到，不同的隱藏單元學會了在影象的不同位置和方向進行邊緣檢測。顯而易見，這些特徵對物體識別等計算機視覺任務是十分有用的。若將其用於其他輸入域（如音訊），該演算法也可學到對這些輸入域有用的表示或特徵。

如果輸入資料中隱含著一些特定的結構，比如某些輸入特徵是彼此相關的，那麼這一演算法就可以發現輸入資料中的這些相關性。事實上，這一簡單的自編碼神經網路通常可以學習出一個跟主元分析（PCA）結果非常相似的輸入資料的低維表示。

1.3稀疏自編碼AE的優化目標和解法

1.3.1損失函式

假設有一組s1個特徵的樣本樣本X={x1,x2,⋯,xm}，經過自編碼網路在L2層和L3層分別成為Y={y1,y2,⋯,ym}，Z={z1,z2,⋯,zm}，其中L1層，L2層，L3層分別有節點s1，s2，s3個，則損失函式可以表示成下面的形式

其中{\rm{J}}\left( {{\rm{W}},{\rm{b}},{\rm{x}}} \right) = \frac{1}{2}z - {x^2}

β是一個超引數，控制稀疏性懲罰因子的權重，ρ也是超引數，叫做稀疏性引數。而KL的定義如下

{\rm{KL}}({\rm{\rho }}||{{\hat \rho }_j}) = {\rm{\rho log}}\frac{\rho }{{{{\hat \rho }_j}}} + \left( {1 - \rho } \right)log\frac{{1 - \rho }}{{1 - {{\hat \rho }_j}}}

而且{{\hat \rho }_j}是L2層的第j個節點的平均啟用度，定義如下

{{\hat \rho }_j} = \frac{1}{{\rm{m}}} \sum \limits_{i = 1}^m \left[ {{y_j}\left( {{\rm{xi}}} \right)} \right]

其中{y_j}\left( {xi} \right)表示L2層的第j個節點在輸入為xi的時候的值.

1.3.2求解

求解步驟如下：

（1）   對於每個訓練樣本x進行迭代：

a)先計算L3層的每一個節點i的誤差

\delta _i^{\left( 3 \right)} = - \left( {{x_i} - {z_i}} \right) \bullet \nabla f\left( {W_i^{\left( 2 \right)}{y_i} + b_i^{\left( 2 \right)}} \right)

得到的結果是L3層的殘差。

再計算L2層的每一個節點i的誤差

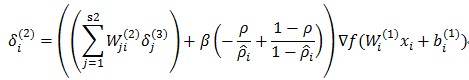
得到的結果是L2層的每個節點i的殘差
b)然後計算{W^{\left( 2 \right)}}和{b^{\left( 2 \right)}}的梯度,利用上面的殘差

\frac{\partial }{{\partial W_{ij}^{\left( 2 \right)}}}J\left( {W,b,x} \right) = {y_j}\delta _i^{\left( 3 \right)}

\frac{\partial }{{\partial b_i^{\left( 2 \right)}}}J\left( {W,b,x} \right) = \delta _i^{\left( 3 \right)}

和{W^{\left( 1 \right)}}和{b^{\left( 1 \right)}}的梯度,利用上面的殘差

\frac{\partial }{{\partial W_{ij}^{\left( 1 \right)}}}J\left( {W,b,x} \right) = {x_j}\delta _i^{\left( 2 \right)}

\frac{\partial }{{\partial b_i^{\left( 1 \right)}}}J\left( {W,b,x} \right) = \delta _i^{\left( 2 \right)}

c)誤差進行累計,l=1,2

\Delta W_{ij}^{\left( l \right)}: = \Delta W_{ij}^{\left( l \right)} + \frac{\partial }{{\partial W_{ij}^{\left( l \right)}}}J\left( {W,b,x} \right)

\Delta b_i^{\left( l \right)}: = \Delta b_i^{\left( l \right)} + \frac{\partial }{{\partial b_i^{\left( l \right)}}}J\left( {W,b,x} \right)

(2)更新{W^{\left( l \right)}}和{b^{\left( l \right)}}的權重

{\rm{W}}_{ij}^{\left( l \right)} = {\rm{W}}_{ij}^{\left( l \right)} - \alpha \left[ {\frac{1}{m}\Delta W_{ij}^{\left( l \right)} + \lambda W_{ij}^{\left( l \right)}} \right]

b_i^{\left( l \right)} = b_i^{\left( l \right)} - \alpha \left[ {\frac{1}{m}\Delta b_i^{\left( l \right)}} \right]


致謝

感謝NG的部落格，無私奉獻了這麼多資料

感謝鄧侃率領的一群人翻譯了NG的部落格的所有內容，讓我等小白能看懂。

Deep Learning高質量交流群裡的多位同學：@廈大_影象_風淳 ，@羅傑 ，@Wilbur


參考文獻

[1]http://deeplearning.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B  NG的部落格，鄧侃翻譯版



from: http://blog.csdn.net/mytestmy/article/details/16918641

相關文章