先來點預備知識。矩陣的3種運算我們稱之為“行初等變換”:
- 交換任意2行
- 某一行的元素全部乘以一個非0數
- 某一行的元素加上另一行對應元素的N倍,N不為0
以矩陣實施行初等變換等同於在矩陣左邊乘以一個矩陣。
當要求矩陣A的逆時,在A的右邊放一個單位矩陣,我們稱[A|I]為增廣矩陣。對增廣矩陣實施行初等變換,即左乘一個矩陣P,如果使得P[A|I]=[PA|P]=[I|P],則P就是$A^{-1}$。
通過一系列的行初等變換把[A|I]變成[I|P]的形式,有很多種途徑,而數值計算就是要找到一種確定性的便於計算機執行的方法,gauss jordan消元法就是這樣一種方法,第i次迭代時,它讓增廣矩陣的第i行乘以一個係數,使得增廣矩陣的第i行第i列上的元素變為1,然後讓第i行以外的其他行加上第i行上對應元素的N倍,使得其他行的第i列上的元素變為0。下面舉例說明gauss_jordan消元法的計算過程。
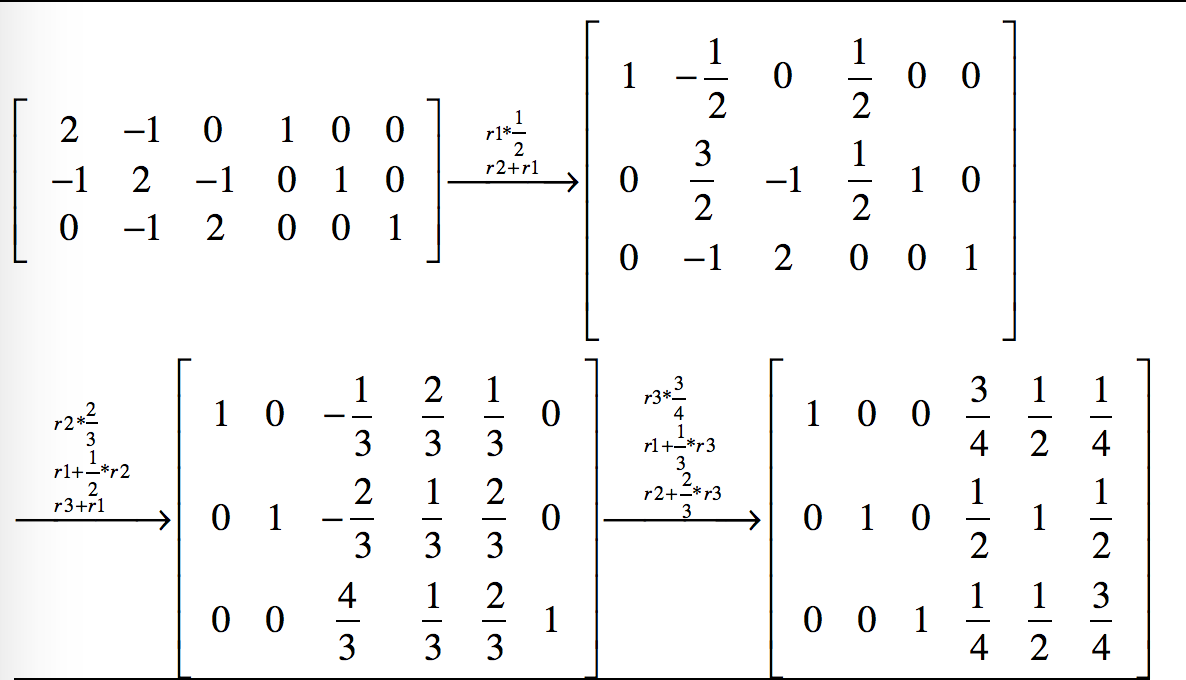
上例中A是一個3階矩陣,所以經過3次迭代得到了它的逆矩陣,每次迭代增廣矩陣中的每個元素(共3行6列18個元素)都要變一次,所以演算法的時間複雜度為$O(2*n^3)$
觀察上面增廣矩陣的變化過程,我們發現在每一步迭代的結果中,增廣矩陣左側有x列已化為單位矩陣時,右側就有n-x列保持著單矩陣的樣子,即總能從增廣矩陣中抽出n列組成一個單矩陣。同時左側已化為單位矩陣的那幾列在以後的行初等變換為始終保持不變。所以,可以把右側不再是單位矩陣的列儲存到左側已變為單矩陣的列上,這樣就不需要額外的記憶體來儲存整個增廣矩陣了,記憶體開銷減少了一半,同時演算法的時間複雜度也降為$O(n^3)$(雖然量級上沒有變化)。
數值計算的迭代過程往往都伴隨著舍入誤差的累積,所以最終的結果也會有誤差,如果這個最終的誤差在一個可控的範圍內,則稱該演算法為數值穩定的演算法,否則為數值不穩定的演算法。什麼時候會造成數值不穩定?比如演算法某一步要除以一個很小的數,小到絕對值趨近於0,商趨於無窮大,此時舍入誤差大到不可控。相對於除以一個很小的數,除以一個很大數是比較安全的,因為真實的商值本來就趨於0,舍入後取0,這個誤差並不大。所以gauss jordan消元法有一種“穩定”的形式,就是“選主元的gauss jordan消元法”。在每一個迴圈過程中,先尋找到主元(即絕對值最大的那個元素),並將主元通過行變換(無需列變換)移動到矩陣的主對角線上,然後將主元所在的行內的所有元素除以主元,使得主元化為1;然後觀察主元所在的列上的其他元素,將它們所在的行減去主元所在的行乘以一定的倍數,使得主元所在的列內、除主元外的其他元素化為0,這樣就使得主元所在的列化為了單位矩陣的形式。這就是一個迴圈內做的工作。然後,在第二輪迴圈的過程中,不考慮上一輪計算過程中主元所在的行和列內的元素,在剩下的矩陣範圍內尋找主元。
選主元的方式雖然使演算法變得非常穩定,但是計算量也明顯上升,一種折中的方法是“選取列主元”,即在第i次迴圈迭代中,從第i列中選主元,同樣第i列中第i行之前的元素不在候選的範圍內。
gauss_jordan.py
# coding=utf-8
__author__ = "orisun"
import numpy as np
EPS = 1.0e-9
'''實現3種初等行變換
'''
def swapRow(A, i, j):
'''交換矩陣A的第i行和第j行
'''
n = A.shape[1]
for x in xrange(n):
tmp = A[i, x]
A[i, x] = A[j, x]
A[j, x] = tmp
def scaleRow(A, i, coef):
'''矩陣A的第i行元素乘以一個非0係數coef
'''
assert abs(coef) > EPS
n = A.shape[0]
for x in xrange(n):
A[i, x] *= coef
def addRowToAnother(A, i, j, coef):
'''把矩陣A第i行的coef倍加到第j行上去
'''
assert abs(coef) > EPS
n = A.shape[0]
for x in xrange(n):
A[j, x] = coef * A[i, x] + A[j, x]
def gauss_jordan_0(mat, column_pivot=True):
'''高斯-約旦法求矩陣的逆。
引數column_pivot為True時將採用列主元消去法。
不會改變輸入矩陣mat。
時間複雜度為O(n^3)
'''
n = mat.shape[0]
# 構建增廣矩陣。這樣需要額外的記憶體空間來儲存一個跟mat同等規模的矩陣
A = np.insert(mat, n, values=np.eye(n), axis=1)
for pivot in xrange(n):
if column_pivot:
# 尋找第pivot列絕對值最大的元素(即列主元),把該元素所在的行與第pivot行進行交換
if(pivot < n - 1):
maxrow = pivot
maxval = abs(A[pivot, pivot])
for row in xrange(pivot + 1, n): # 只需要從該列的第pivot個元素開始往下找
val = abs(A[row, pivot])
if(val > maxval):
maxval = val
maxrow = row
if(maxrow != pivot):
swapRow(A, pivot, maxrow)
# 第pivot行乘以一個係數,使得A[pivot,pivot]變為1
coef = 1.0 / A[pivot, pivot]
if abs(coef) > EPS:
for col in xrange(pivot, 2 * n):
A[pivot][col] *= coef
# 把第pivot行的N倍加到其他行上去,使得第pivot列上除了A[pivot,pivot]外其他元素都變成0
for row in xrange(n):
if row == pivot:
continue
coef = 1.0 * A[row, pivot]
if abs(coef) > EPS:
for col in xrange(pivot, 2 * n):
A[row, col] -= coef * A[pivot, col]
# 取出增廣矩陣的右半部分即為A的逆
return A[:, n:]
def gauss_jordan(A, column_pivot=True):
'''高斯-約旦法求矩陣的逆。
引數column_pivot為True時將採用列主元消去法。
該方法經了優化,不需要額外的記憶體空間來儲存增廣矩陣。但是會改變原始的輸入矩陣A,最終A變成了它自身的逆。由於沒有增廣矩陣,計算量至少減少為原來的一半。
時間複雜度為O(n^3)
'''
n = A.shape[0]
for pivot in xrange(n):
# 構建n行1列的B矩陣,它的第pivot行上為1,其他全為0
B = np.array([[0.0] * n]).T
B[pivot, 0] = 1.0
if column_pivot:
# 尋找第pivot列絕對值最大的元素(即列主元),把該元素所在的行與第pivot行進行交換
if(pivot < n - 1):
maxrow = pivot
maxval = abs(A[pivot, pivot])
for row in xrange(pivot + 1, n): # 只需要從該列的第pivot個元素開始往下找
val = abs(A[row, pivot])
if(val > maxval):
maxval = val
maxrow = row
if(maxrow != pivot):
swapRow(A, pivot, maxrow)
swapRow(B, pivot, maxrow)
# 第pivot行乘以一個係數,使得A[pivot,pivot]變為1
coef = 1.0 / A[pivot, pivot]
if abs(coef) > EPS:
for col in xrange(0, n):
A[pivot, col] *= coef
B[pivot, 0] *= coef
# 把第pivot行的N倍加到其他行上去,使得第pivot列上除了A[pivot,pivot]外其他元素都變成0
for row in xrange(n):
if row == pivot:
continue
coef = 1.0 * A[row, pivot]
if abs(coef) > EPS:
for col in xrange(0, n):
A[row, col] -= coef * A[pivot, col]
B[row, 0] -= coef * B[pivot, 0]
# 把B儲存到A的第pivot列上去
for row in xrange(n):
A[row, pivot] = B[row, 0]
# 此時的A已變成了原A的逆
return A
def test():
import time
from numpy import random
from scipy import linalg
import math
n = 100 #n上千時用就不適合用gauss_jordan法了,半天算不出結果
arr = random.randint(100, size=(n, n))
begin = time.time()
gauss_jordan(arr, False)
end = time.time()
print 'gauss_jordan use time ', end - begin
# 矩陣規模很小時gauss_jordan法更快。矩陣規模稍大時linalg.inv更快。
# begin = time.time()
# linalg.inv(arr) #使用linalg.inv經常無法求解,因為隨機構造出來的矩陣經常是奇異矩陣
# end = time.time()
# print 'linalg.inv use time ', end - begin
if __name__ == '__main__':
test()
print "original"
A = np.array([[2, -1, 0], [-1, 2, -1], [0, -1, 2]], dtype='d')
print A
print "inverse matrix"
print gauss_jordan_0(A, True)
print "inverse matrix"
print gauss_jordan(A, True)
print "swap row1 and row2"
swapRow(A, 1, 2)
print A
print "row1 multiple by -0.5"
scaleRow(A, 1, -0.5)
print A
稍大一些的矩陣求逆就不適合用gaussJordan法了(實際上很多大型矩陣的運算都不能用課本上講的方法直接求解),大型稀疏矩陣求逆是很多論文裡關注的焦點問題,常見的方法是GMRES。
說明一下通過解方程求逆矩陣的理論依據:$Ax=I$ => $A(x_1|x_2|...|x_n)=(I_1|I_2|...|I_n)$ => $Ax_1=I_1,\ Ax_2=I_2,\ Ax_n=I_n$
其中$x_i$是矩陣$x$的第i列,$I_i$是單位矩陣$I$的第i列。$x=A^{-1}$。我們可以解一次方程$Ax=I$直接得到$x$,但這種“省事”的方法可能產生記憶體溢位。我們也可以解n個方程$Ax_1=I_1,\ Ax_2=I_2,\ Ax_n=I_n$,最後把$x_i$拼在一起構成$x$,這樣不存在記憶體溢位的問題,但是計算十分耗時。折中的方法是每次解方程求出$x$的一部分,即解$Ax_{i...j}=I_{i...j}$
solve_matrix.py
# coding=utf-8
__author__ = "orisun"
import numpy as np
from scipy.linalg import lu, solve # 建議使用scipy.linalg取代numpy.linalg
from scipy.sparse import lil_matrix, dok_matrix, coo_matrix
from scipy.sparse.linalg import gmres, lgmres, spsolve, inv # 專門用來求解稀疏係數矩陣方程組
import time
from numpy import random
if __name__ == '__main__':
n = 1000 # 上萬維時LU分解直接記憶體溢位
arr = random.random(size=(n, n))
begin = time.time()
x, l, u = lu(arr) # LU分解
end = time.time()
print 'LU decomposition use time ', end - begin
# 二維矩陣建議使用numpy.array,不要使用numpy.matrix
A = np.array([[2, -1, 0], [-1, 2, -1], [0, -1, 2]], dtype='d')
b = np.eye(3)
print '解方程', solve(A, b) # 通過解方程的方式也可以求逆
print '解方程', spsolve(A, b) # 稀疏矩陣解方程
print '求逆', inv(lil_matrix(A)) # 稀疏矩陣求逆(要求原矩陣必須非奇異)
b = np.array([[1, 0, 0]]).T
print '解方程', gmres(A, b, tol=1e-08, maxiter=1)[0] # 稀疏矩陣解方程
print '解方程', lgmres(A, b, tol=1e-08, maxiter=1)[0] # lgmres比gmres收斂性好一些
print
# 使用spsolve解方程的方式對大型稀疏矩陣求逆(原矩陣可以是奇異的)
n = 7000
arr = lil_matrix((n, n))
arr[0, 165] = 1.0
arr[135, 138] = 1.0
arr[545, 388] = 1.0
arr[998, 578] = 1.0
arr[13, 455] = 9.0
b = np.eye(n)
begin = time.time()
spsolve(arr, b) # 稀疏矩陣解方程
end = time.time()
print 'spsolve use time ', (end - begin) # n=7000時耗時1秒
捎帶說一句,求逆矩陣另外一種常用的方法是LU分解,時間複雜度跟Gauss-Jordan法相同,都是$n^3$。如果只是做矩陣分解,LU分解法大約需要執行$\frac{n^3}{3}$次內層迴圈(每次包括一次乘法和一次加法)。這是求解一個(或少量幾個)右端項時的運算次數,它要比Gauss-Jordan消去法快三倍,比不計算逆矩陣的Gauss-Jordan法快1.5倍。當要求解逆矩陣時,總的運算次數(包括向前替代和回代部分)為$n^3$,與Gauss-Jordan法相同。