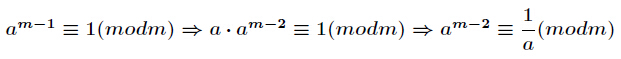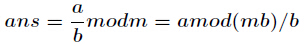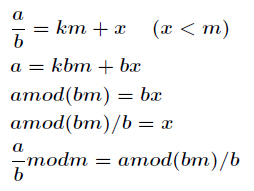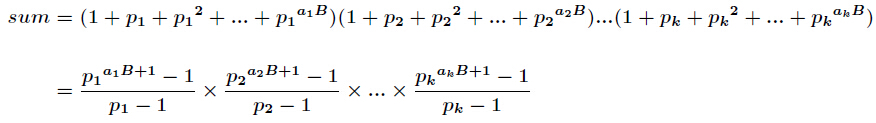逆元學習

bigbigship發表於2014-09-10

定義：對於正整數和，如果有，那麼把這個同餘方程中的最小正整數解叫做模的逆元。

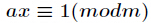
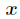
逆元一般用擴充套件歐幾里得演算法來求得，如果為素數，那麼還可以根據費馬小定理得到逆元為。

 

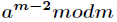
推導過程如下

                            

 

求現在來看一個逆元最常見問題，求如下表示式的值（已知）

 

           

 

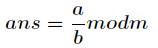
當然這個經典的問題有很多方法，最常見的就是擴充套件歐幾里得，如果是素數，還可以用費馬小定理。

 

但是你會發現費馬小定理和擴充套件歐幾里得演算法求逆元是有侷限性的，它們都會要求與互素。實際上我們還有一

種通用的求逆元方法，適合所有情況。公式如下

 

          

 

現在我們來證明它，已知，證明步驟如下

 

          

例題POJ1845  http://poj.org/problem?id=1845

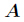
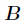
題意：給定兩個正整數和，求的所有因子和對9901取餘後的值。

 

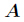
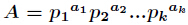
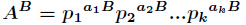
分析：很容易知道，先把分解得到，那麼得到，那麼

     的所有因子和的表示式如下

 

    


方法一：二分求等比數列和：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
//#define debug
using namespace std;

typedef long long LL;

const int MOD = 9901;
const int maxn = 10005;

int p[maxn],cnt;
int num[maxn];
bool prime[maxn];

void isprime()
{
    cnt = 0;
    memset(prime,true,sizeof(prime));
    for(int i=2; i<maxn; i++)
    {
        if(prime[i])
        {
            p[cnt++] = i;
            for(int j=i+i; j<maxn; j+=i)
                prime[j] = false;
        }
    }
}

/*void fenjie(int n)
{
    cnt=0;
    memset(p,0,sizeof(p));
    for(int i=2;i*i<=n;i++){
        if(n%i==0) p[cnt]=i;
        while(n%i==0)
            num[cnt]++;
        cnt++;
    }
    if(n!=1){
        p[cnt]=n;
        num[cnt++]=1;
    }
}*/

LL quick_mod(LL a,LL b)
{
    LL ans=1;
    while(b){
        if(b&1){
            ans=ans*a%MOD;
            b--;
        }
        b>>=1;
        a=a*a%MOD;
    }
    return ans;
}

LL sum(LL a,LL n)
{
    if(n==0) return 1;
    LL t=sum(a,(n-1)/2);
    if(n&1){
        LL tmp=quick_mod(a,(n+1)/2);
        t=(t+t%MOD*tmp%MOD)%MOD;
    }
    else{
        LL tmp=quick_mod(a,(n+1)/2);
        t = (t + t % MOD * tmp % MOD) % MOD;
        t = (t + quick_mod(a,n)) % MOD;
    }
    return t;
}

void solve(LL a,LL b)
{
    //fenjie(a);
    isprime();
    LL ans=1;
    #ifdef debug
    cout<<"*****************"<<endl;
    for(int i=0;i<cnt;i++)
        cout<<p[i]<<" "<<num[i]<<endl;
    cout<<"*****************"<<endl;
    #endif // debug
    for(int i=0;p[i]*p[i]<=a;i++){
        if(a%p[i]==0){
            int num=0;
            while(a%p[i]==0)
                num++,a/=p[i];
            ans*=sum(p[i],num*b)%MOD;
            ans%=MOD;
        }
    }
    if(a>1)
        ans*=sum(a,b)%MOD;
    printf("%lld\n",ans%MOD);
}
int main()
{
    LL a,b;
    while(~scanf("%lld%lld",&a,&b)){
        solve(a,b);
    }
    return 0;
}

方法二：求逆元+等比數列求和公式 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
//#define debug
using namespace std;

typedef long long LL;

const int MOD = 9901;
const int maxn = 10005;

int p[maxn],cnt;
int num[maxn];
bool prime[maxn];

void isprime()
{
    cnt = 0;
    memset(prime,true,sizeof(prime));
    for(int i=2; i<maxn; i++)
    {
        if(prime[i])
        {
            p[cnt++] = i;
            for(int j=i+i; j<maxn; j+=i)
                prime[j] = false;
        }
    }
}

LL multi(LL a,LL b,LL m)
{
    LL ans=0;
    while(b){
        if(b&1){
            ans=(ans+a)%m;
            b--;
        }
        b>>=1;
        a=(a+a)%m;
    }
    return ans;
}

LL quick_mod(LL a,LL b,LL m)
{
    LL ans=1;
    while(b){
        if(b&1){
            ans=multi(ans,a,m);
            b--;
        }
        b>>=1;
        a=multi(a,a,m);
    }
    return ans;
}

void solve(LL a,LL b)
{
    isprime();
    LL ans=1;
    for(int i=0;p[i]*p[i]<=a;i++){
        if(a%p[i]==0){
            int num=0;
            while(a%p[i]==0)
                num++,a/=p[i];
            LL M = (p[i]-1)*MOD;
            ans*=(quick_mod(p[i],num*b+1,M)+M-1)/(p[i]-1);
            ans%=MOD;
        }
    }
    if(a>1){
        LL M=(a-1)*MOD;
        ans*=(quick_mod(a,b+1,M)+M-1)/(a-1);
        ans%=MOD;
    }
    printf("%lld\n",ans);
}

int main()
{
    LL a,b;
    while(~scanf("%lld%lld",&a,&b)){
        solve(a,b);
    }
    return 0;
}


相關文章