HDU3944 DP? (LUCAS定理+階乘預處理)

bigbigship發表於2014-07-28
Problem Description

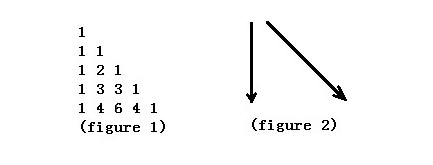
Figure 1 shows the Yang Hui Triangle. We number the row from top to bottom 0,1,2,…and the column from left to right 0,1,2,….If using C(n,k) represents the number of row n, column k. The Yang Hui Triangle has a regular pattern as follows.
C(n,0)=C(n,n)=1 (n ≥ 0) 
C(n,k)=C(n-1,k-1)+C(n-1,k) (0<k<n)
Write a program that calculates the minimum sum of numbers passed on a route that starts at the top and ends at row n, column k. Each step can go either straight down or diagonally down to the right like figure 2.
As the answer may be very large, you only need to output the answer mod p which is a prime.
 

Input
Input to the problem will consists of series of up to 100000 data sets. For each data there is a line contains three integers n, k(0<=k<=n<10^9) p(p<10^4 and p is a prime) . Input is terminated by end-of-file.
 

Output
For every test case, you should output "Case #C: " first, where C indicates the case number and starts at 1.Then output the minimum sum mod p.
 

Sample Input
1 1 2
4 2 7





 



Sample Output




Case #1: 0
Case #2: 5
題目分析：要求計算最小的和，
當 k < n/2 時需要將C(N,K) 化成 C(N,N-K);
原式 C(N,K)+C(N-1,K-1)+...+C(N-K,0)+K;
由 C(N-1,K)+C(N-1,K-1)=C(N,K) 原式可化為C(N+1，K)+K;
然後經過Lucas定理+對階乘的預處理即可得出結果；
程式碼如下：
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

const int N = 10005;

bool prime[N];

int p[N],f[N][N],inv[N][N],cnt,pth[N];

void isprime(){
    cnt=0;
    memset(prime,1,sizeof(prime));
    for(int i=2;i<N;i++){
        if(prime[i]){
            p[++cnt]=i;
            pth[i]=cnt;
            for(int j=i+i;j<N;j+=i)
                prime[j]=0;
        }
    }
}

int quick_mod(int a,int b,int m){
    int ans=1;
    a%=m;
    while(b){
        if(b&1){
            ans=ans*a%m;
            b--;
        }
        b>>=1;
        a=a*a%m;
    }
    return ans;
}

void init(){//預處理階乘與逆元
    int i,j;
    for(int i=1;i<=cnt;i++){
        f[i][0]=inv[i][0]=1;
        for(int j=1;j<p[i];j++){
            f[i][j]=(f[i][j-1]*j)%p[i];
            inv[i][j]=quick_mod(f[i][j],p[i]-2,p[i]);
        }
    }
}

int com(int n,int m,int P){
    if(m>n) return 0;
    if(m==n) return 1;
    int t=pth[P];
    return f[t][n]*(inv[t][n-m]*inv[t][m]%P)%P;
}

int lucas(int n,int m,int P){
    if(m==0) return 1;
    return com(n%P,m%P,P)*lucas(n/P,m/P,P)%P;
}
int main()
{
    int cas=1,n,m,P;
    isprime();
    init();
    while(cin>>n>>m>>P){
        if(m<=n/2) m=n-m;
        n++;
        printf("Case #%d: %d\n",cas++,(m%P+lucas(n,m+1,P))%P);
    }
    return 0;
}






            




相關文章