Codeforces Round #316 (Div. 2) E dp

連結：戳這裡

Peppa the Pig was walking and walked into the forest. What a strange coincidence! The forest has the shape of a rectangle, consisting of n rows and m columns. We enumerate the rows of the rectangle from top to bottom with numbers from 1 to n, and the columns — from left to right with numbers from 1 to m. Let's denote the cell at the intersection of the r-th row and the c-th column as (r, c).

Initially the pig stands in cell (1, 1), and in the end she wants to be in cell (n, m). Since the pig is in a hurry to get home, she can go from cell (r, c), only to either cell (r + 1, c) or (r, c + 1). She cannot leave the forest.

The forest, where the pig is, is very unusual. Some cells of the forest similar to each other, and some look very different. Peppa enjoys taking pictures and at every step she takes a picture of the cell where she is now. The path through the forest is considered to be beautiful if photographs taken on her way, can be viewed in both forward and in reverse order, showing the same sequence of photos. More formally, the line formed by the cells in order of visiting should be a palindrome (you can read a formal definition of a palindrome in the previous problem).

Count the number of beautiful paths from cell (1, 1) to cell (n, m). Since this number can be very large, determine the remainder after dividing it by 109 + 7.

Input
The first line contains two integers n, m (1 ≤ n, m ≤ 500) — the height and width of the field.

Each of the following n lines contains m lowercase English letters identifying the types of cells of the forest. Identical cells are represented by identical letters, different cells are represented by different letters.

Output
Print a single integer — the number of beautiful paths modulo 109 + 7.

Examples
input
3 4
aaab
baaa
abba
output
3
Note
Picture illustrating possibilities for the sample test.

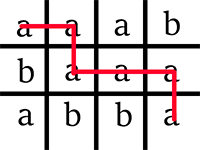
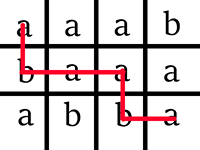
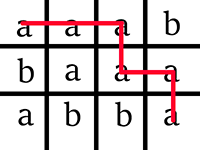
題意：

給出n*m的矩陣的字元，問從(1,1)走到(n,m)走過的字元是迴文串的方案數（每次只能往下或右）

思路：

(1,1)右或下 和 (n,m)左或上 同時開始走，所有走的長度是一樣的，那麼直接判斷當前的s[x1][y1]?==s[x2][y2]

設定dp狀態：dp[len][x1][y1][x2][y2]

表示當前走的路程長度為len,(1,1)走到了點(x1,y1) (n,m)走到了點(x2,y2) 的方案數

然後轉移方程也就是(x1,y1)從兩個方向過來，(x2,y2)兩個方向過來，總共四種情況

但是這裡會超空間，可以發現y1,y2都是可以同x1,x2得到的，所以dp方程變成dp[len][x1][x2]

但是還是會超，注意這裡的長度為len只與len-1有關，所以用滾動陣列變成dp[2][x1][x2]

具體看程式碼

程式碼：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<vector>
#include <ctime>
#include<queue>
#include<set>
#include<map>
#include<stack>
#include<iomanip>
#include<cmath>
#define mst(ss,b) memset((ss),(b),sizeof(ss))
#define maxn 0x3f3f3f3f
#define MAX 1000100
///#pragma comment(linker, "/STACK:102400000,102400000")
typedef long long ll;
typedef unsigned long long ull;
#define INF (1ll<<60)-1
using namespace std;
#define mod 1000000007
int dp[2][550][550];
char s[550][550];
int n,m;
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
    if(s[1][1]==s[n][m]) dp[0][1][n]=1;
    else dp[0][1][n]=0;
    int now=0,last=1;
    int len=(n+m-2)/2;
    for(int i=1;i<=len;i++){
        swap(now,last);
        mst(dp[now],0);
        for(int x1=1;x1<=i+1;x1++){
            for(int x2=n;x2>=n-i;x2--){
                int y1=i-x1+2;
                int y2=n+m-x2-i;
                if(x1>x2 || y1>y2) continue;
                if(s[x1][y1]==s[x2][y2]){
                    dp[now][x1][x2]=(dp[now][x1][x2]+dp[last][x1][x2])%mod;///(x1,y1-1)(x2,y2+1)
                    dp[now][x1][x2]=(dp[now][x1][x2]+dp[last][x1-1][x2])%mod;///(x1-1,y1)(x2,y2+1)
                    dp[now][x1][x2]=(dp[now][x1][x2]+dp[last][x1][x2+1])%mod;///(x1,y1-1)(x2+1,y2)
                    dp[now][x1][x2]=(dp[now][x1][x2]+dp[last][x1-1][x2+1])%mod;///(x1-1,y1)(x2+1,y2)
                }
            }
        }
    }
    int ans=0;
    for(int i=1;i<=n;i++)
        ans=(ans+dp[now][i][i])%mod;
    if((n+m)%2==1){
        for(int i=1;i<n;i++){
            ans=(ans+dp[now][i][i+1])%mod;
        }
    }
    cout<<ans<<endl;
    return 0;
}