Codeforces Round #361 (Div. 2) E 費馬小

連結：戳這裡

Mike wants to prepare for IMO but he doesn't know geometry, so his teacher gave him an interesting geometry problem. Let's define f([l, r]) = r - l + 1 to be the number of integer points in the segment [l, r] with l ≤ r (say that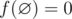). You are given two integers n and k and n closed intervals [li, ri] on OX axis and you have to find:

In other words, you should find the sum of the number of integer points in the intersection of any k of the segments.

As the answer may be very large, output it modulo 1000000007 (109 + 7).

Mike can't solve this problem so he needs your help. You will help him, won't you?

Input
The first line contains two integers n and k (1 ≤ k ≤ n ≤ 200 000) — the number of segments and the number of segments in intersection groups respectively.

Then n lines follow, the i-th line contains two integers li, ri ( - 109 ≤ li ≤ ri ≤ 109), describing i-th segment bounds.

Output
Print one integer number — the answer to Mike's problem modulo 1000000007 (109 + 7) in the only line.

Examples
input
3 2
1 2
1 3
2 3
output
5
input
3 3
1 3
1 3
1 3
output
3
input
3 1
1 2
2 3
3 4
output
6
Note
In the first example:

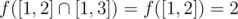
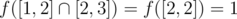
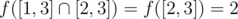
So the answer is 2 + 1 + 2 = 5.

題意：

給出n,k n個區間[l,r] 

問任意k個區間交的區間長度的總長度是多少、

思路：

統計區間覆蓋的個數，然後類似差分陣列的方法統計出區間的覆蓋次數

那麼答案肯定是累加C(num,k)

取模用的是費馬小

程式碼：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<vector>
#include <ctime>
#include<queue>
#include<set>
#include<map>
#include<stack>
#include<iomanip>
#include<cmath>
#define mst(ss,b) memset((ss),(b),sizeof(ss))
#define maxn 0x3f3f3f3f
#define MAX 1000100
///#pragma comment(linker, "/STACK:102400000,102400000")
typedef long long ll;
typedef unsigned long long ull;
#define INF (1ll<<60)-1
#define mod 1000000007
using namespace std;
struct node{
    int x,v;
    node(int x=0,int v=0):x(x),v(v){}
    bool operator < (const node &a)const{
        return x<a.x;
    }
}a[1000100];
ll fac[1000100];
ll ppow(ll k,ll n) {
    ll c=1;
    while(n) {
        if(n%2) c=(c*k)%mod;
        k=(k*k)%mod;
        n>>=1;
    }
    return c;
}
ll C(ll a,ll b) {
    return (((fac[b]*ppow((fac[a]*fac[b-a])%mod,mod-2)))%mod)%mod;
}
int n,K;
int main(){
    fac[0]=1;
    for(int i=1;i<=200000;i++) fac[i]=(fac[i-1]*i)%mod;
    scanf("%d%d",&n,&K);
    int cnt=0;
    for(int i=1;i<=n;i++){
        int l,r;
        scanf("%d%d",&l,&r);
        a[cnt++]=node(l-1,1);
        a[cnt++]=node(r,-1);
    }
    sort(a,a+cnt);
    ll last=-1e10,num=0,ans=0;
    for(int i=0;i<cnt;i++){
        if(num>=K) ans+=C(K,num)*((ll)a[i].x-last)%mod;
        ans%=mod;
        num+=a[i].v;
        last=a[i].x;
    }
    printf("%I64d\n",ans);
    return 0;
}